遗传算法c++实现_【电力大数据】基于遗传算法的电能表配送计划优化研究

计量中心采用人工方式制定配送计划,由于电能表库存在空间和时间上的分布不均匀,导致即使配送需求100%满足,仍然存在表不够用的情况。本文针对配送计划开展数学建模,应用遗传算法优化配送计划,确保各市县公司安全库存偏差最小,有效提升各市县公司的电能表库存均匀性。
01
电力计量设备配送现状及存在问题
在电网公司,电能表一般由省计量中心集中配送,电能表从计量中心配送出库到现场安装的主要过程梳理如下:

图1:表计流转示意图
配送计划由计量中心计划员制定,在制定计划时,应尽可能满足各市县公司的配送时间和配送数量的需求。
当不能同时满足各单位的配送时间需求时,一般采用提前配送、先报先配的原则。省计量中心集中配送的模式,存在配送单位数量多、电能表配送总量大的情况。
以某省计量中心为例,配送单位近100个,每年配送出去的电能表平均总量多达330万只。尽管已100%满足各市县公司配送需求,但是由于用户的用表需求无法及时满足而导致的投诉事件仍然时有发生。为什么配送需求100%满足却仍存在“表不够用”的情况呢?
02
“表不够用”的原因分析
根据库存管理理论,为防止未来物资供应或需求的不确定性因素(如大量突发性订货、交货意外中断或突然延期等),需设置安全库存下限;为防止发生超额库存成本,需设置安全库存上限。
某省电力公司设定需求单位的库存上限为运行电能表数量的3%,库存下限为运行电能表数量的1%,也可以直接用库存运行比上下限来表示库存上下限。
库存运行比=(合格在库电能表数量/运行电能表数量)*100%
经统计,某省电力公司2017年12月底各单位库存运行比情况,如下图所示:

图2:2017年全省库存运行比统计
通过以上数据分析,全省库存运行比均值为2.95%,在库存上下限范围内,但是方差为2.95%,说明库存分布较不均衡。图中也可直观看出,有的地市高于库存上限,有的地市低于库存下限,从而导致有的地方无表可用,有的地方却库存积压。
经统计,某地市公司2017年全年库存运行比情况,如下图所示:
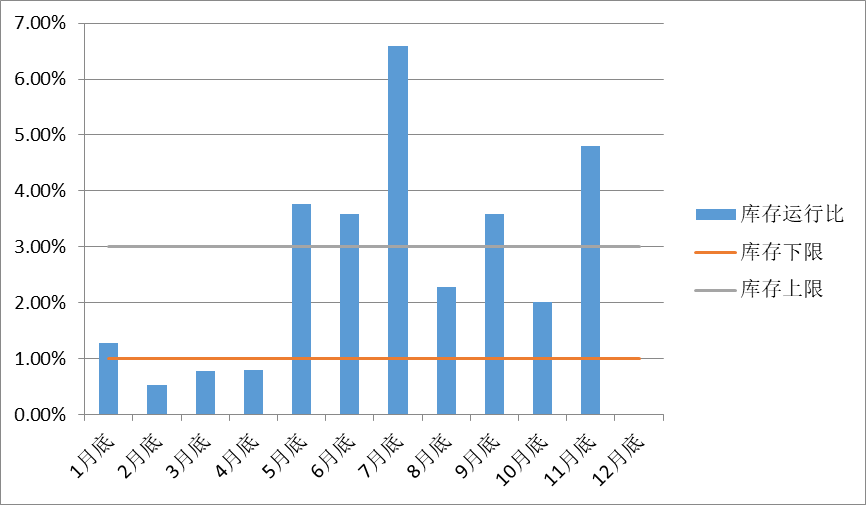
图3:某地市2017年库存运行比统计
通过以上数据分析,某地市公司全年库存运行比均值为2.57%,在库存上下限范围内,方差为1.91%,说明时间分布较不均衡。图上也可以直观反应出有几个月低于库存下限,有几个月高于库存上限,从而导致有时无表可用,有时却库存积压。
库存运行比在时间和空间上分布不均匀是导致配送需求100%满足却仍存在“表不够用”情况的主要原因。那么,如何在完成月度配送计划的前提下,保障各单位库存运行比在库存上下限范围内呢?
03
配送计划优化建模
为维持各单位库存运行比处在1%至3%的上下限范围内,如何通过配送调控各单位仓库安全库存偏差最小是关键。
因此,配送计划优化目标为:以满足各地市配送需求为前提,结合计量中心库存、配送运力以及地市单位当前库存,制定配送计划,使得各市县公司安全库存偏差最小。依据配送计划优化目标,开展数据建模,模型中涉及的参数有:
1.日配送量(设为X,变量值);
2.安全库存偏差度(设为P,目标值,计算日配送量X使P值最小);
3.各单位现有库存量(设为M,已知值,可从系统获取);
4.各单位安全库存下限(设为CI,常量值,可由运行量和库存运行比下限计算得出);
5.安全库存上限(设为CM,常量值,可由运行量和库存运行比上限计算得出);
6.计量中心各品规设备理论库存量(设为Q,考虑了检定对库存量的补充);
7.计量中心每天运力(设为T,常量);
8.地市单位月度需求总量(设为R);
某单位i第d天的安全库存偏差度可表述为:
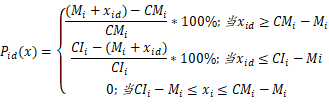
全省当月库存计划造成的库存安全偏差度则可表述为:
其中,i代表某单位,m代表总需求单位个数;d代表某天,n代表当月天数;而求配送量x值使得目标函数f(x)最小,便是本次建模的目标。
每天配送量x又应满足以下约束条件:
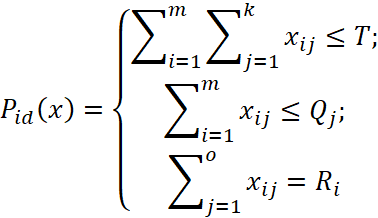
其中,j代表某品规,k代表品规设备种类数量。
求每个使P最小,即计算单位i品规j的配送量,使配送当天全省需求单位库存安全偏差最小。
04
计量配送计划优化算法实现
以上数学模型有多种算法求最优解,常用的有遗传算法、模拟退火算法、爬山算法、粒子群算法、蚁群算法等。
(1)遗传算法:优点是能很好的处理约束,能很好的跳出局部最优,最终得到全局最优解,全局搜索能力强;缺点是收敛较慢,局部搜索能力较弱,运行时间长,且容易受参数的影响。
(2)模拟退火算法:优点是局部搜索能力强,运行时间较短;缺点是全局搜索能力差,容易受参数的影响。
(3)爬山算法:显然爬山算法较简单,效率高,但是处理多约束大规模问题时力不从心,往往不能得到较好的解。
(4)粒子群算法:适合求解实数问题,算法简单,计算方便,求解速度快,但是存在着陷入局部最优等问题。
(5)蚁群算法:适合在图上搜索路径问题,计算开销会比较大。
月度配送计划一般每月制定一次,每周进行调整,对实时性要求比较低。另外,配送计划不仅要满足配送需求,同时受到计量中心库存和运力的约束。经综合考虑,采用遗传算法求解最合适。
遗传算法实际上是一种随机搜索算法,它模仿染色体对变量进行编码,随机生成大量个体,应用适应性函数(目标函数)进行选择,通过基因变异不断迭代,逐渐得到最优解。
根据遗传算法的基本原理,我们首先对日计量配送方案进行编码,编码格式如下:

图4:基因编码
日配送方案是由每一辆配送车辆的装载方案组成,如果一个配送方案表示一个个体的话,那么每一辆车的装载方案表示个体的一个基因。装载方案中包含配送单位,品规,配送数量等信息。
按照遗传算法的原理,配送计划优化过程如下:
(1)种群初始化。
a、随机取一个单位,获取该单位的配送需求;
b、按照安全库存偏差和品规权重排序,将Car1装满,如果该单位总需求小于Car1的载货量,全部装载;
c、重复1~2直至将Car1到Car10都装上货;
d、重复1~3生成1500个个体。
(2)自然选择
a、根据配送计划优化目标函数,计算安全偏差,安全偏差越大,适应度越低;
b、对安全偏差从小到大排列,淘汰排名后80%的个体,保留排名前20%的个体;
c、复制优胜的个体繁殖子代,优胜者的前20%,子代占总子代的35%;第二个20%,占25%;第三个20%,占20%;第三个20%,占15%;第四个20%,占5%。
(3)基因变异。
由于配送数量不能超过需求总量,所以基因之间存在约束。基因交叉会破坏约束关系,在本课题实践中不采用交叉方式变异,只采用突变方式。
a、随机获取一个变异位置Cari;
b、将Cari上的货物卸载,重新加入需求清单;
c、随机获取一个配送的单位;
d、将该单位的需求设备装到Cari上。
(4)获取一天最佳配送方案
a、循环迭代40代;
b、将适应度排名第一的个体作为最终解;
c、更新配送需求清单。
(5)获取月度最佳配送方案。
重复(1)~(3)的过程,直至配送需求清零。
以上过程中的种群数量,基因突变率,优胜率,迭代次数等参数,在实施过程中需平衡算法性能和优化效率进行调优。
05
优化效果
算法上线后,经计量中心配送计划员测试,3分钟之内能完成月底计划的自动拟定,相比原手工拟定需要一天的时间,效率大大提升,自动拟定计划效果如下图所示:
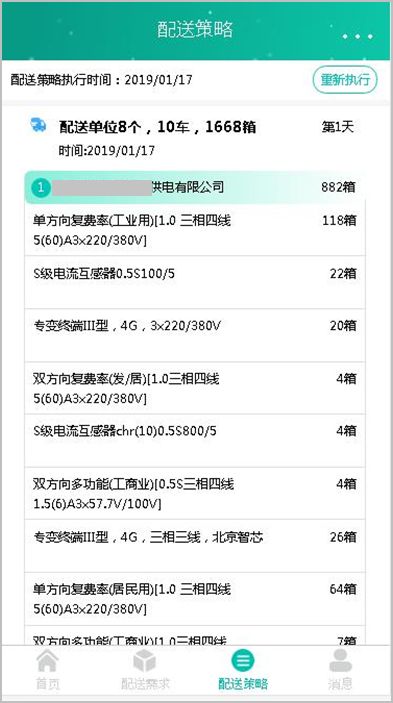
图5:配送计划效果图
经过一年的运行,某省电力公司,2018年12月底各单位库存运行比情况,如下图所示:
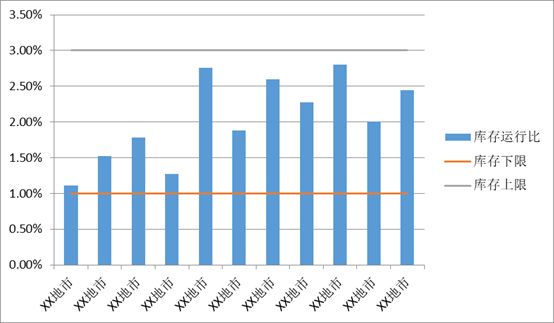
图6:2018年全省库存运行比统计
通过以上数据分析,全省库存运行比均值为2.04%在库存上下限范围内,每个地市也都在库存上下限范围内。
方差为0.59%,相比优化前2.95%明显减少,说明库存分布较为均衡。
经统计某地市公司,2018年年库存运行比情况,如下图所示:

图7:某地市2018年库存运行比统计
通过以上数据分析,某地市公司全年库存运行比均值为2.24%在库存上下限范围内,每个月的库存运行比也基本都在库存上下限范围内。
方差为0.65%,相比优化前的1.91%明显降低,说明时间分布较为均衡。
从实际应用效果来看,截止2018年底,因不及时装表的投诉次数相比2017年减少70%以上。
06
结语
本配送计划优化算法主要考虑了库存安全性,还是有一些值得改进的地方:一是由于缺少库存动态预测功能,随着时间推移,实际库存和预测库存的偏差越来越大,因此,与计划制定当天时间距离越远的配送方案优化效果越差。二是未考虑配送线路规划和零碎配送顺带的情况,对降低配送成本没有效果。期待下次更多交流。
【阮贤希|朗新科技集团 营业计量业务部】
注:文章仅代表作者观点,欢迎转发和评论。转发、转载、转帖等须注明“稿件来源:朗新研究院”违者朗新研究院将依法追究责任,谢谢!
推荐阅读
浅析电力企业产品的轻量化设计
福利来啦|PPT~电力现货市场中售电公司如何构建核心竞争力
【能源服务】数据赋能,助力综合能源业务市场拓展
智能化时代全业务自助电力无人营业厅探索
亲测有效:让电力产品交互设计更流畅的四个原则
【技术分享】区块链技术在电网公司物资管理中的应用探索