《算法笔记》学习日记——8.2 广度优先搜索(BFS)
目录
- 8.2 广度优先搜索(BFS)
-
- 问题 A: Jugs
- 问题 B: DFS or BFS?
- 问题 C: 【宽搜入门】8数码难题
- 问题 D: 【宽搜入门】魔板
- 问题 E: 【宽搜入门】巧妙取量
- 小结
8.2 广度优先搜索(BFS)
Codeup Contest ID:100000609
前排提示:本篇文章字数较多,请选择性观看,主要的字数在于思路和代码。
问题 A: Jugs
题目描述
In the movie “Die Hard 3”, Bruce Willis and Samuel L. Jackson were confronted with the following puzzle. They were given a 3-gallon jug and a 5-gallon jug and were asked to fill the 5-gallon jug with exactly 4 gallons. This problem generalizes that puzzle.
You have two jugs, A and B, and an infinite supply of water. There are three types of actions that you can use: (1) you can fill a jug, (2) you can empty a jug, and (3) you can pour from one jug to the other. Pouring from one jug to the other stops when the first jug is empty or the second jug is full, whichever comes first. For example, if A has 5 gallons and B has 6 gallons and a capacity of 8, then pouring from A to B leaves B full and 3 gallons in A.
A problem is given by a triple (Ca,Cb,N), where Ca and Cb are the capacities of the jugs A and B, respectively, and N is the goal. A solution is a sequence of steps that leaves exactly N gallons in jug B. The possible steps are
fill A
fill B
empty A
empty B
pour A B
pour B A
success
where “pour A B” means “pour the contents of jug A into jug B”, and “success” means that the goal has been accomplished.
You may assume that the input you are given does have a solution.
输入
Input to your program consists of a series of input lines each defining one puzzle. Input for each puzzle is a single line of three positive integers: Ca, Cb, and N. Ca and Cb are the capacities of jugs A and B, and N is the goal. You can assume 0 < Ca <= Cb and N <= Cb <=1000 and that A and B are relatively prime to one another.
输出
Output from your program will consist of a series of instructions from the list of the potential output lines which will result in either of the jugs containing exactly N gallons of water. The last line of output for each puzzle should be the line “success”. Output lines start in column 1 and there should be no empty lines nor any trailing spaces.
样例输入
3 7 1
9 32 6
样例输出
fill B
pour B A
empty A
pour B A
success
fill B
pour B A
empty A
pour B A
empty A
pour B A
empty A
pour B A
fill B
pour B A
empty A
pour B A
empty A
pour B A
empty A
pour B A
empty A
pour B A
fill B
pour B A
empty A
pour B A
empty A
pour B A
success
提示
倒水问题的经典形式是这样的:
“假设有一个池塘,里面有无穷多的水。现有2个空水壶,容积分别为5升和6升。问题是如何只用这2个水壶从池塘里取得3升的水。”
当然题外是有一些合理的限制的,比如从池塘里灌水的时候,不管壶里是不是已经有水了,壶一定要灌满,不能和另一个壶里的水位比照一下“毛估估”(我们可以假设壶是不透明的,而且形状也不同);同样的,如果要把水从壶里倒进池塘里,一定要都倒光;如果要把水从一个壶里倒进另一个壶里,也要都倒光,除非在倒的过程中另一个壶已经满了;倒水的时候水没有损失(蒸发溢出什么的)等等等等。
事实上,要解决上面这题,你只要用两个壶中的其中一个从池塘里灌水,不断地倒到另一个壶里,当第二个壶满了的时候,把其中的水倒回池塘里,反复几次,就得到答案了。以5升壶(A)灌6升壶(B)为例:
A B
0 0
5 0 A→B
0 5
5 5 A→B
4 6
4 0 A→B
0 4
5 4 A→B
3 6
现在我们问,如果是多于2只壶的情况怎么办(这样一来就不能用上面的循环倒水法了)?如何在倒水之前就知道靠这些壶是一定能(或一定不能)倒出若干升水来的?试举数例:
1) 两个壶:65升和78升,倒38升和39升。
2) 三个壶:6升,10升和45升,倒31升。
我们可以看到,在1)中,65=5×13,78=6×13,而39=3×13。所以如果把13升水看作一个单位的话(原题中的“升”是没有什么重要意义的,你可以把它换成任何容积单位,毫升,加仑——或者“13升”),这题和最初的题目是一样的。而38升呢?显然是不可能的,它不是13的倍数,而65升和78升的壶怎么也只能倒出13升的倍数来。也可以这样理解:这相当于在原题中要求用5升和6升的壶倒出38/39升来。
那么2)呢?你会发现,只用任何其中两个壶是倒不出31升水的,理由就是上面所说的,(6,10)=2,(6,45)=3,(10,45)=5,(这里(a,b)是a和b的最大公约数),而2,3,5均不整除31。可是用三个壶就可以倒出31升:用10升壶四次,6升壶一次灌45升壶,得到1升水,然后灌满10升壶三次得30升水,加起来为31升。
一般地我们有“灌水定理”:
“如果有n个壶容积分别为A1,A2,……,An(Ai均为大于0的整数)设w为另一大于0的整数。则用此n个壶可倒出w升水的充要条件为:
1) w小于等于A1+A2+…+An;
2) w可被(A1,A2,…,An)(这n个数的最大公约数)整除。”
这两个条件都显然是必要条件,如果1)不被满足的话,你连放这么多水的地方都没有。2)的道理和上面两个壶的情况完全一样,因为在任何步骤中,任何壶中永远只有(A1,A2,…,An)的倍数的水。
现在我们来看一下充分性。在中学里我们学过,如果两个整数a和b互素的话,那么存在两个整数u和v,使得ua+vb=1。证明的方法很简单:在对a和b做欧几里德辗转相除时,所有中间的结果,包括最后得到的结果显然都有ua+vb的形式(比如第一步,假设a小于b,记a除b的结果为s,余数为t,即b=sa+t,则t=(-s)a+b,即u=-s,v=1)。而两个数互素意味着欧几里德辗转相除法的最后一步的结果是1,所以1也可以记作ua+vb的形式。稍微推广一点,如果(a,b)=c,那么存在u和v使得ua+vb=c(两边都除以c就回到原来的命题)。
再推广一点,如果A1,A2,……,An是n个整数,(A1,A2,…,An)=s,那么存在整数U1,U2,……,Un,使得
U1A1 + U2A2 + … + UnAn = s. (*)
在代数学上称此结果为“整数环是主理想环”。这也不难证,只要看到
(A1,A2,A3,A4,…,An) = ((((A1,A2),A3),A4),…,An).
也就是说,可以反复应用上一段中的公式:比如三个数a,b,c,它们的最大公约数是d。假设(a,b)=e,那么(e,c)=((a,b),c)=d。现在有u1,u2使得u1a+u2b=e,又有v1,v2使得v1e+v2c=d,那么
(v1u1)a+(v1u2)b+(v2)c=d.
好,让我们回头看“灌水定理”。w是(A1,A2,…,An)的倍数,根据上节的公式(*),两边乘以这个倍数,我们就有整数V1,V2,……,Vn使得 V1A1 + V2A2 + … + VnAn = w.注意到Vi是有正有负的。
这就说明,只要分别把A1,A2,……,An壶,灌上V1,V2,……,Vn次(如果Vi是负的话,“灌上Vi次”要理解成“倒空-Vi次”),就可以得到w升水了。具体操作上,先求出各Vi,然后先往Vi是正数的壶里灌水,灌1次就把Vi减1。再把这些水到进Vi是负数的壶里,等某个壶灌满了,就把它倒空,然后给这个负的Vi加1,壶之间倒来倒去不变更各Vi的值。要注意的是要从池塘里灌水,一定要用空壶灌,要倒进池塘里的水,一定要是整壶的。这样一直到所有Vi都是0为止。
会不会发生卡住了,既不能灌水又不能倒掉的情况?不会的。如果有Vi仍旧是负数,而Ai壶却没满:那么如果有其它Vi是正的壶里有水的话,就都倒给它;如果有其它Vi是正的壶里没水,那么就拿那个壶打水来灌(别忘了给打水的壶的Vi减1);如果根本没有任何Vi是正的壶了——这是不可能的,这意味着w是负的。有Vi仍旧是正数,而Ai壶却没满的情况和这类似,你会发现你要用到定理中的条件1)。
这样“灌水定理”彻底得证。当然,实际解题当中如果壶的数目和容积都比较大的话,手工来找(*)中的各Ui比较困难,不过可以写个程序,连倒水的步骤都算出来。最后要指出的一点是,(*)中的Ui不是唯一的,所以倒水的方式也不是唯一的。
思路
ZOJ上AC了,但是Codeup上还是答案错误50,我也不知道是哪儿错了……
这题在ZOJ上的地址:
Jugs
这题的在思路上很简单,就是用BFS搜索6个方向(empty A/empty B/fill A/fill B/pour A B/pour B A)。
我的解题方法是:每次把点(x,y)代表成是A杯中剩余的水(x)和B杯中剩余的水(y),这样的话,就能把这个问题简化为坐标点的问题了。那么何时结束BFS呢?就是当纵坐标y==n的时候,就说明B杯中剩余的水已经达到了你输入的要求n,就return了。
以上就是这题的大致思路。但是,想要AC还得经历重重磨难(切身体会!!小坑太多了!!我从前一天晚上做到了第二天中午,当然,第二天是周末,睡到十点钟才起的……),下面我来说一下这题的坑点:
①必须做剪枝处理,因为每次都要搜索6个方向,就好像一棵树一样,第一个起点往外发出6个方向的分叉,然后每个分叉又能往外发出6个方向,即便是BFS也承受不了这么大的一棵树,如果不剪枝的话,内存一定会超限(题目一般要求3MB(Codeup)~6MB(ZOJ)),而且就算内存还在题目范围内,那搜索时间也是巨慢无比的(复杂度:O(6n))。因此,我做了如下剪枝处理:1.当A杯本身就是空的时候,就不能再执行empty A的操作(B杯同理);2.当A杯本身是满的时候,就不能再执行fill A的操作(B杯同理);3.当A杯是空的,亦或者B杯是满的时候,不再执行pour A B的操作(pour B A同理)。这样,就剪掉了一些无用的“杂枝”,但是还不够,虽然他们不会去执行那句对应的if语句,但还是会入队,因此,就需要做第二步的剪枝处理;
②设一个bool型二维数组判断是否已入队,这就是刚才所提到的第二步剪枝处理,每次需要判断当前操作出来的点是否已经入过队,如果没有,那么按正常的程序走,入队,如果之前已经入过队了,那就什么都不干,前往另外一个“岔路口”走。如果不加这个判断的话,就会造成许多无用点来来回回一直在入队,也给程序造成了不小的负担;
③事实证明,不管是Codeup还是ZOJ,应该都是多点测试的,因此,在printf(“success\n”);之后,一定要清空你的数组(保险起见,不管是全局还是局部,只要是在main()函数里用到过的,都清空),否则只能正确运行第一组数据,第二组压根不会输出(ZOJ上就是segmentation fault(段错误),我一开始以为是二维数组不够大,在这里卡了很久,其实是第一组数据处理完之后没有清空用到的数组)。
除了这些坑,这题还要求输出路径,如果用BFS的话,那就要每次记录当前点的前驱,然后就能通过BFS结束时的终点一直找前驱找到起点。我的方法是从终点开始,把每个点都入栈,这样的话,当所有点入栈完毕,再依次出栈的时候,就是正常输出路径的顺序了。但是这题要求的所谓路径是操作方法,因此我把六种操作方法对应0~5放在了一个结构体里面,具体可以看代码的实现。
最后,这题题目说了给的数据一定是有解的,所以也不用考虑无解的情况了。当然,这题也有不用BFS实现的更简单的方式,具体可以看别的大佬的代码。
另外,这里说一下二维数组用memset的清空方法,比之前我用for循环二维数组的行数,然后每行memset的方法快很多:
memset(数组名,0,n*m);
这里的n和m分别是二维数组的第一维长度和第二维长度(n行m列)。
代码
#include问题 B: DFS or BFS?
题目描述
说好了,题目不黑人。
给你一个8*8的矩阵,你的初始位置是左下角方格(用’U’表示),你的目标位置是右上角的方格(用’A’表示),其余的62个方格,如果是’.’,表示这个方格为空,如果是’S’,表示这个方格有一块大石头。好了现在你开始从左下角出发,每次可以往上,下,左,右,左上,右上,左下,右下移动一个方格,或者你可以原地不动,一共九个动作方式,在你做完一个动作后,所有的大石头会往下掉一个方格(如果一个大石头的位置是(x,y),那下一秒是(x+1,y),不过如果它已经在最下面的一排了,那它就会掉出矩阵,不再出现),请注意,任一时刻,你不能和某一个大石头处在同一个方格,否则石头会把你XX掉。
现在的问题就是:你能从左下角安全抵达右上角么? 如果能,输出“Yes”,反之,“No”。
输入
T->测试数据组数(T)。
对于每组数据,输入一个8*8的矩阵,其后有一空行。描述如上。
输出
对于第i组数据,请输出
Case #i: s(s是一个字符串,如果可以到达,则s为“Yes”,反之“No”)
样例输入
2
.......A
........
........
........
........
........
........
U.......
.......A
........
........
........
........
.S......
S.......
US......
样例输出
Case #1: Yes
Case #2: No
思路
思路参考了【漫浸天空的雨色】(我一开始的思路比较直白,判断到终点再return,现在想想看如果不判重的话,要一直走到终点可能这个程序已经爆了……因为每次都是9个枝节,从左下走到右上得9n次方这么多,因此得找到隐藏条件早点结束掉BFS),尽管如此,但做的时候还是遇到了不少困难,虽然样例早早地就过了,但一直卡在答案错误50%这个地方,直到看到了这篇文章:
【慧丫儿】
里面提到了这题最大的陷阱就是不能判重,这句话可以说是关键中的关键了(感谢这位大佬,解救了我一直卡着的问题),因为书上写的缘故,以及上一题Jugs的缘故,我习惯性地为了防止枝节过多而设了个二维数组判重(就是一个二维bool数组判断是否已经入队,这样就可以不走重复路),但是这题不同于迷宫问题,因为没过一个动作,石头就往下掉一层,因此,只要找到空位“狗住”,无论是走过的还是没走过的,只要一直狗到石头掉完(最多8个动作,无论石头在哪都会掉完),就一定能走到终点,但是如果不走重复路的话,可能就少了些“狗住”的机会,而导致被石头砸中死掉,最终造成答案错误。
再次再次感谢这两位大佬!!这两篇文章都给了我莫大的帮助Thanks♪(・ω・)ノ
代码
#include问题 C: 【宽搜入门】8数码难题
题目描述
![]()
初始状态的步数就算1,哈哈
输入:第一个3*3的矩阵是原始状态,第二个3*3的矩阵是目标状态。
输出:移动所用最少的步数
Input
2 8 3
1 6 4
7 0 5
1 2 3
8 0 4
7 6 5
Output
6
思路
这题因为自己的蠢交了学费了T T(实在想不通错在哪儿了,花了20买了题库,结果发现题库除了样例只有一个测试数据,而且因为不知道搜索的过程,只知道答案不对,所以还是不知道错哪儿了……),至于我是怎么发现自己的错误呢,我在网上找了个8数码难题的PPT,里面把一个样例用BFS搜索的每一步都写了出来,然后我就干脆每次遍历四个方向的时候,就打印一步,最终发现中间某一步多了个数据,才知道自己的越界判断函数没写对(爆哭),就在这卡了整整一个晚上和一个上午的时间,哎……下次写搜索类的题目一定要细心啊!!!
思路是很简单的,甚至可以说这题是个水题,首先我们要明白的是,BFS记录的一定是状态(比如第一题Jugs我们记录的是两杯水中水量的状态,第二题中我们记录的是结点的状态),因此,这题最直观的思路就是记录经过每一步变换的矩阵的状态(比如第一步,我把0往上移动,形成了一个状态,入队,往左移动,又形成了一个状态,入队,往右移动,又形成了一个状态,再入队,BFS的精髓就是把每次移动出来的可能性状态全部入队),但是这里直接把二维矩阵入队又不好操作。我的思路是这样的:把这个二维矩阵展开成一维的字符串,那么无非就是在0~8的全排列里面找。
于是,我们只要设置一个队列,里面是字符串即可(queue
然后还有判重问题,这里用map就好了,设置string到bool型的映射。另外,我也验证过了,如果直接对一个未出现的字符串判断(比如map[“我还没出现过”]),那么它的值是false,所以放心的用就可以了。
这题我觉得最重要的还是细心吧,我就是把它展开成一维字符串之后偷懒了(懒得对9个数的移动情况一一判断,因为我一开始看的是矩阵中间那个数,然后又看了一个中间上面的那个数,因为上下左右移动都很正常,感觉只要在字符串范围内就行了,于是就把judge函数写好了,结果就因为这个破问题卡了半天……),没有对9个位置的全部情况进行判断,而导致BFS的判断过程出现了错误,进一步导致了提前出现最优解,哎,做这类搜索题目的时候一定要细心细心再细心!!
代码
#include问题 D: 【宽搜入门】魔板
题目描述
在成功地发明了魔方之后,鲁比克先生发明了它的二维版本,称作魔板。这是一张有8个大小相同的格子的魔板:
1 2 3 4
8 7 6 5
我们知道魔板的每一个方格都有一种颜色。这8种颜色用前8个正整数来表示。可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,沿顺时针方向依次取出整数,构成一个颜色序列。对于上图的魔板状态,我们用序列(1,2,3,4,5,6,7,8)来表示。这是基本状态。
这里提供三种基本操作,分别用大写字母“A”,“B”,“C”来表示(可以通过这些操作改变魔板的状态):
“A”:交换上下两行;
“B”:将最右边的一列插入最左边;
“C”:魔板中央四格作顺时针旋转。
下面是对基本状态进行操作的示范:
A:
8 7 6 5
1 2 3 4
B:
4 1 2 3
5 8 7 6
C:
1 7 2 4
8 6 3 5
对于每种可能的状态,这三种基本操作都可以使用。
你要编程计算用最少的基本操作完成基本状态到目标状态的转换,输出基本操作序列。
【输入格式】
输入有多组测试数据
只有一行,包括8个整数,用空格分开(这些整数在范围 1——8 之间),表示目标状态。
【输出格式】
Line 1: 包括一个整数,表示最短操作序列的长度。
Line 2: 在字典序中最早出现的操作序列,用字符串表示,除最后一行外,每行输出60个字符。
Sample Input
2 6 8 4 5 7 3 1
Sample Output
7
BCABCCB
思路
这和上一题差不多,思路还是把这个2*4的矩阵展开为一维的字符串来存储,但是这题还要求输出最求解的路径,我还是跟问题A:Jugs一样,采用记录父结点的方式,然后同时记录操作数,最后通过结果一直找父亲就能找到最优解的路径了,然后通过压栈和出栈来输出正序的路径。
其实我很早就把样例过了,但是狂用map的我超时了,然后就进入了一个无底深渊……不是时间超限88,就是运行错误88,我一直不解的是,为什么最开始用完全用map还是会运行错误(运行错误不是一般都是因为指针乱指或者数组越界嘛??有知道的大佬可以告诉我一下吗,万分感谢!!),然后我个人估计是在map里用string映射比较耗时,于是就用8进制转10进制的方法把每个状态的字符串转换成10进制的整数来hash,然后这里又犯了一个很蠢的错误,写进制转换函数的时候,写成这样了:
id = id * 8 +(a[i]-'0');//8进制转10进制
这对于0~7的数字是没问题的,但是题目给的是1~8,因此还需要减1,所以应该这么写:
id = id * 8 +(a[i]-'0'-1);//8进制转10进制
但是坑还远远没有结束……我全部把原来map中的string型改成int型之后,有一个点会改变:那就是原封不动的情况,原来如果map映射string的话,原封不动的情况是没问题的,输入基础状态,就会输出0,但是改用int型hash之后,这种情况就需要特判来另外输出。
然而我一直以为还是map的问题导致时间太长,于是想了各种办法:改cin、cout为scanf、printf;改endl为’\n’;以及用数组来代替map(因为反正是int型之间的映射,完全可以用数组来)。然而一不小心改多了,改了三个maxn的数组,于是又内存超限了(因为用8进制到10进制的话,maxn至少要8^8这么大,一个maxn大的数组还能接受,三个就超限了)。然后就一直有问题,一直解决不了,因为我觉得既然之前原封不动的情况能正常输出,改了int型hash应该也能正常输出,所以一直没去试,搞得很烦躁。直到有一次试着输入了一下目标即是基本状态的情况,才发现程序报错了,特判输出之后就AC了。
哎……心累啊┓(;´_`)┏以后出错的时候还是要多考虑考虑边界值,即便改之前是正常的(谁知道改了以后会不会出错呢,是叭)。
代码里我就没有写用数组的情况了,因为maxn的数组内存占用太大了,而且还有很多无效空间浪费,还不如map。
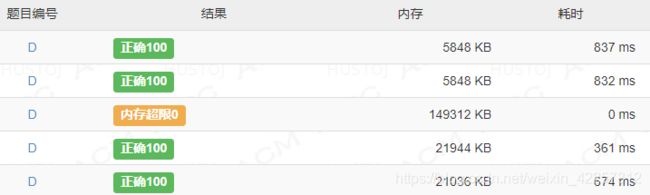
这张图是分别用map和数组的情况(5000多KB的是3个map,20000多KB的是1个maxn数组和2个map),内存超限那个是3个maxn数组的情况:
代码
#include里的reverse()函数把tmp逆置
int id = getid(tmp.str);
if(inq[id]==false){
//如果未曾入队
father[id] = getid(top.str);
cz[id] = 0;//记录操作(这里记录的是操作后得到的子串,所以子串对应当前的操作)
tmp.step = top.step+1;
if(tmp.str==a.str) return tmp;//如果已经完成目标了,返回步数
q.push(tmp);
inq[id] = true;
}
}
if(i==1){
//操作B:将最右边的一列插入最左边
tmp.str = changeB(top.str);
int id = getid(tmp.str);
if(inq[id]==false){
//如果未曾入队
father[id] = getid(top.str);
cz[id] = 1;//记录操作
tmp.step = top.step+1;
if(tmp.str==a.str) return tmp;//如果已经完成目标了,返回步数
q.push(tmp);
inq[id] = true;
}
}
if(i==2){
//操作C:魔板中央四格作顺时针旋转
tmp.str = changeC(top.str);
int id = getid(tmp.str);
if(inq[id]==false){
//如果未曾入队
father[id] = getid(top.str);
cz[id] = 2;//记录操作
tmp.step = top.step+1;
if(tmp.str==a.str) return tmp;//如果已经完成目标了,返回步数
q.push(tmp);
inq[id] = true;
}
}
}
}
}
int main(){
string target;
while(cin>>target){
for(int i=1;i<=7;i++){
string tmp;
cin>>tmp;
target += tmp;
}
if(target==initial) cout<<0<<'\n';
else{
Rubiks_Magic e, result;
stack<int> path;//记录路径
e.str = target;
e.step = 0;
result = bfs(e);
cout<<result.step<<'\n';
int exit = getid(result.str);//得到最终的字符串(也就是题目输入的)
path.push(cz[exit]);
while(1){
exit = father[exit];//找到当前字符串的父亲串
if(exit==getid(initial)) break;//如果等于基本状态了,break
//因为在这里子串和操作是一一对应的,cz[exit]代表着exit由什么操作而来,因此不需要知道基本状态由什么操作而来
path.push(cz[exit]);//找到对应的操作数入栈
}
while(!path.empty()){
cout<<action[path.top()];//从栈顶输出操作路径
path.pop();
}
cout<<'\n';
inq.clear();
father.clear();
cz.clear();
}
}
return 0;
}
问题 E: 【宽搜入门】巧妙取量
题目描述
【题目描述】
有三个容器,容量分别为 a,b,c(a> b > c ),一开始a装满油,现在问是否只靠abc三个容器量出k升油。如果能就输出“yes”,并且说明最少倒几次,否则输出“no”。例如:10升油在10升的容器中,另有两个7升和3升的空容器,要求用这三个容器倒油,使得最后在abc三个容器中有一个刚好存有5升油,问最少的倒油次数是多少?(每次倒油,A容器倒到B容器,或者A内的油倒完,或者B容器倒满。
10 7 3
(10 0 0)
(3 7 0):第一次
(3 4 3):第二次
(6 4 0):第三次
(6 1 3):第四次
(9 1 0):第五次
(9 0 1):第六次
(2 7 1):第七次
(2 5 3):第八次,出现5了。
Input
【输入格式】
有多组测试数据。
输入a,b,c, k四个正整数( 100 ≥ a > b > c≥1 , 1≤k< 100 )
Output
【输出格式】
如果能得到k就输出两行。
第一行“yes”,第二行为最少的次数
否则输出“no”
Sample Input
10 7 3 5
Sample Output
yes
8
思路
这题和问题A:Jugs差不多,在这里我说一下不同点:①本题是3个杯子,所以要用一个三维的点(x,y,z)来记录每个状态;②这题不用记录操作路径,比Jugs简单一点;③容易漏掉的一个方面:在两个杯子互相倒的时候,一定要继承那个无关容器的水量,比如A和B之间倒水,新捏出来的cup tmp一定要继承队首元素中C的水量,即:
tmp.z = top.z
否则状态之间的变换会出错(因为状态涉及到三个量,而倒水只涉及到两个量)。
最后想说的是,这题的测试点怪怪的,我样例能过,而且把样例的k改成别的数也能正确输出次数,但就是答案错误0,好歹这次早点看到了【蠢叶】大佬的博客
里面提到了还要判倒0次的情况,比如样例输入给10 7 3 10的话,那就应该输出0次。但是正常的bfs是输出不出来的,所以要特判,于是特判输出之后就直接AC了。
提醒一下自己:边界值我又忘了-_-||,这类题目一定要注意注意再注意边界值呀。
代码
#include小结
感觉做BFS的题目是一种磨练吧,我从礼拜五开始做,差不多这三天里的大部分时间都在做这一节的题目,我普遍经历的痛苦是这样的:①刚开始没输出,用单步调试进入BFS函数看哪儿错了;②算法改对之后有输出了,样例也过了,结果内存超限(或时间超限);③于是进行优化剪枝,剪完之后就是普普通通的答案错误(抓狂W( ̄_ ̄)W)……
于是我得出一个结论,做BFS类的题目一定要细心,最好把边界情况什么的写在纸上,提醒自己,千万不要写着写着又忘了,然后卡着一个边界测试点一直过不去,东改西改,死也改不对,搞得情绪又非常暴躁,然后恶性循环,越暴躁又越想不出正确的思路来。
BFS其实不难,但是还是要多练的,比如我做第一个题目的时候就做得泪流满面……对于我这种一次BFS都没写过的新手来说实在是太磨人了,按顺序写到最后一题的时候,我跟着思路一遍BFS写下来基本上就AC了,其实也就那么点东西,无非就是在BFS里“岔路口”的处理要进行优化剪枝,否则这棵BFS树会异常庞大,时间肯定会超限,然后就是判重问题,这就要看具体情况了,有些题目要判重(大部分都要,否则重复的状态入队也会耗时很久),而有的又不用(比如问题B:DFS or BFS?),另外,应该灵活抓住题目的条件,来缩减搜索的范围(同理,如问题B:DFS or BFS?,如果硬要搜到终点位置的话,耗时不堪设想,题目只要求判断能否活着到终点,而地图里的石头又是会掉出矩阵的,因此只要存在能呆到某个时刻石头掉光的情况,就能活着到终点)。
另外,从倒数第二题魔板得出的结论:用map映射string耗时严重。
建议看一下这篇博文:
关于set/map 等容器对string类的 性能指标
如果想偷懒用string,但又怕超时,最优的应该是unordered_set,当然,用进制转换的方法变成int型再用map我觉得是最简单又好用的一个办法。