回溯算法
常规来说,回溯算法和动态规划算法是面试中笔试考的相对比较多的两个算法,区别就是在于一个可以重头再来一个可以无限读档,本篇专栏将来看看回溯算法是如何做到无限重来的。。
回溯算法常见的考的题型有:数独、八皇后、0-1背包、图的着色、旅行商问题和全排列等等。。。
如何理解回溯算法
之前介绍的贪心算法和分治算法无非就是让策略最优化,贪心算法可以使我们每次进行选择的时候选择看起来是最优的选择,分治算法可以将大问题化成小问题从而逐一解决,进而降低难度,回溯算法则类似于遍历所有的解法从中选出最优的解法。
举个例子来说一下:
现在有一个8*8的棋盘,希望往里面放八个旗子,每个棋子所在的行列对角线都不能有另一个棋子。。
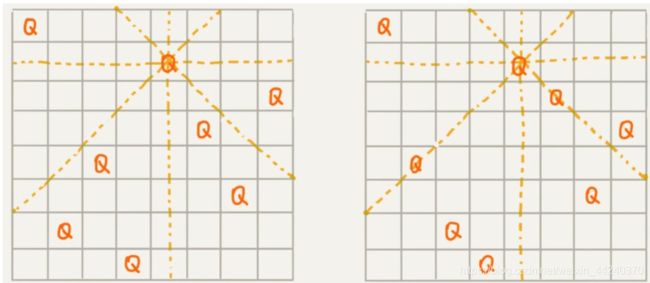
左边第一张图就是满足条件的,第二张图就是不满足条件的,想要解决问题需要这么几个步骤:
- 首先将第一个棋子放在第一行某个位置
- 然后放第二个棋子在满足条件的第二行的某个位置
- 不断循环,然后就可以满足条件了。。
回溯算法适合用递归来实现,用下面的代码来实现这个题目:
package sufang;
/**
* 回溯法
*/
public class Queen {
public static int num = 0; //累计方案
public static final int MAXQUEEN = 8;
public static int[] cols = new int[MAXQUEEN]; //定义cols数组,表示8列棋子皇后摆放的位置
/**
*
* @param n 填第n列的皇后
*/
public void getCount(int n){
boolean[] rows = new boolean[MAXQUEEN]; //记录每个方格是否可以放皇后
for (int m =0;m<n;m++){
rows[cols[m]] = true;
int d = n - m; //斜对角,d为差距
//正斜方向
if (cols[m]-d >=0){
rows[cols[m]-d] = true;
}
//反斜方向
if (cols[m]+d <= (MAXQUEEN-1)){
rows[cols[m]+d] = true;
}
}
//到此知道了哪些位置不能放皇后
for (int i=0;i<MAXQUEEN;i++){
if (rows[i]){
continue; //不能放
}
cols[n] = i;
//下面可能有仍然合法的位置
if (n<MAXQUEEN-1){
getCount(n+1);
}else {
//找到完整一套方案
num ++;
printQueen();
}
}
}
private void printQueen() {
System.out.println("第"+num+"种方案");
for (int i=0;i<MAXQUEEN;i++){
for (int j=0;j<MAXQUEEN;j++){
if (i == cols[j]){
System.out.print("0 ");
}else {
System.out.print("M ");
}
}
System.out.println();
}
}
public static void main(String[] args) {
Queen queen = new Queen();
queen.getCount(0);
}
}
理解上述代码之后再来说两个例子联系一个回溯算法的应用和实现。。
0-1背包问题
0-1背包问题是经典的dp算法题,但是使用回溯法也是可以解决的,0-1背包有很多变体,先来介绍一下最基础的。。
假设有一个背包,背包的承载重量是Mkg,现在有n个物品,每个物品的重量不相等且不可分割,现在需要选择装载到背包,如何在不超过装载重量的情况下使背包中的物品总重量最大。
这时大家可能会想到使用贪心算法,但是贪心算法解决的问题是东西有重复且可以将东西拆分放入,进而获取到最大价值,但是0-1背包问题显然不是这样设计的,之所以说是0-1背包问题,是因为这个东西要么装要么不装。。。
实际上,对于每种物品来说,都有两种选择,装或者不装。所以对于n个物品共有2^n种选择,只需要在策略中选择最接近Mkg的即可。。。
首先将物品依次排列,这样问题分为了n个阶段每个阶段操作一个物品,装或者不装,然后递归处理剩下的物品。。
来看一下代码:
package sufang;
public class BagZeroOne {
private int maxM = 0; //存储背包中物品总重量的最最大值
/**
*
* @param i 表示考察到哪个物品了
* @param cw 表示已经装进去的物品的重量和
* @param w 背包重量
* @param items 表示每个物品的重量
* @param n 表示物品数
* 假设背包可以承受重量是100, 物品个数是10, 物品重量存储在数组a中
* 然后这样调用函数f(0, 0, a, 10, 100)
*/
private void f(int i, int cw, int[] items, int n, int w){
if (cw == w || i == n){
//cw == w表示装满;i==n表示已经考察完所有物品
if (cw > maxM)
maxM = cw;
return;
}
f(i+1, cw, items, n ,w);
System.out.println(cw);
if (cw + items[i] <= w){
已经超过可以背包承受的重量的时候,就不装了
f(i+1, cw + items[i], items, n, w);
}
}
public static void main(String[] args) {
int[] a = {
1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
new BagZeroOne().f(0, 0, a, 10, 100);
}
}
正则表达式
对于一个工程师来说的话,通配符是很重要的知识点,将一些符号串在一起表达丰富的语意。假设正则表达式中国只包含*和?两种通配符,并且对这两种通配符的语意稍微做些改变。。
其中 “ * ”可以匹配任意多个(大于等于0个)任意字符,“?”匹配零个或者一个任意字符。然后根据定死的文本,能否给定正则表达式。
依次考察正则中的每个字符,非通配符就直接和文本进行匹配,如果相同就继续往下处理,如果不同就回溯。
如果遇到特殊字符,也就是岔路口,有很多种方案,去组合使用两种通配符,当无法继续匹配就从最近的断点重新来。
下面来看一下代码:
package sufang;
public class Pattern {
private boolean matched = false;
private char[] pattern;//正则表达式
private int plen; //正则表达式长度
public Pattern(char[] pattern, int plen) {
this.pattern = pattern;
this.plen = plen;
}
public boolean match(char[] text, int tlen) {
//文本串及其长度
matched = false;
rmatch(0, 0, text, tlen);
return matched;
}
private void rmatch(int ti, int pj, char[] text, int tlen) {
if (matched) return;//如果已经匹配好了,就不要继续递归了
if (pj == plen) {
//正则表达式到结尾了
if (pj == plen) matched = true;//文本串也到结尾了
return;
}
if (pattern[pj] == '*') {
//匹配任意个字符
for (int k = 0; k <= tlen - ti; ++k) {
rmatch(ti + k, pj + 1, text, tlen);
}
} else if (pattern[pj] == '?') {
//匹配0或者1个字符
rmatch(ti,pj+1,text,tlen);
rmatch(ti+1,pj+1,text,tlen);
} else if (ti < tlen && pattern[pj] == text[ti]) {
//纯字符匹配才行
rmatch(ti+1,pj+1,text,tlen);
}
}
public static void main(String[] args) {
char[] chars = {
'*', '?'};
char[] chars1 = {
'z', 'h'};
System.out.println(new Pattern(chars, 2).match(chars, 2));
}
}
总结
回溯思想在于大部分情况下都是用广义的去搜索问题,就是从一组可能的解中选择出一个满足要求的解。而施加更具体的条件可以使复杂度降低。。。