2021寒假每日一题《01背包问题》

01背包问题

题目来源：背包九讲
时间限制：1000ms 内存限制：64mb

题目描述

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品 只能使用一次 。
第 $i$ 件物品的体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，$N$，$V$，用空格隔开，分别表示物品数量和背包容积。
接下来有 $N$ 行，每行两个整数 $v_i$,$w_i$，用空格隔开，分别表示第 $i$ 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0 < $N$,$V$ ≤ 1000
0 < $v_i$,$w_i$ ≤ 1000

样例输入

4 5
1 2
2 4
3 4
4 5

样例输出

8

解题思路1：暴力破解

尝试各种可能的商品组合，并找出价值最高的组合。
使用 $N$ 位二进制字串表示物品是否放入背包，枚举所有的可能，然后算出每种可能的价值，取其最大值输出。
解法不足：速度非常慢。在只有3件商品的情况下，你需要计算8个不同的集合；当有4件商品的时候，你需要计算16个不同的集合。每增加一件商品，需要计算的集合数都将翻倍。
对于每一件商品，都有选或不选两种可能，即这种算法的运行时间是 $O(2^n)$ 。
IO竞赛（例如：蓝桥杯）当中，如果实在想不起来动态规划，可以使用这个方法拿到一部分分数，但是在ACM竞赛当中，就不能使用这种方法了。

解题代码1-Java

import java.util.*;

public class Main {
     
    static int getSum(int n, int v, StringBuilder binString, int[][] items) {
     
        int sumV = 0, sumN = 0;
        for (int j = 0; j < n; j++) {
     
            if (binString.charAt(j) == '1') {
     
                sumV += items[j][0];
                sumN += items[j][1];
            }
            if (sumV > v) {
     
                return -1;
            }
        }
        return sumN;
    }

    public static void main(String[] args) {
     
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int v = input.nextInt();
        int totalV = 0, totalN = 0;
        int[][] items = new int[n][2];
        for (int i = 0; i < n; i++) {
     
            items[i][0] = input.nextInt();
            items[i][1] = input.nextInt();
            totalV += items[i][0];
            totalN += items[i][1];
        }
        input.close();
        if (totalV <= v) {
     
            System.out.println(totalN);
            return;
        }
        int sumN = 0;
        for (long i = 0; i < Math.pow(2, n); i++) {
     
            StringBuilder binString = new StringBuilder(Long.toBinaryString(i));
            long len = binString.length();
            while (len < n) {
     
                binString.insert(0, "0");
                len++;
            }
            sumN = Math.max(sumN, getSum(n, v, binString, items));
        }
        System.out.println(sumN);
    }
}

解题思路2：动态规划

对于动态规划算法，可以去这篇文章里学习：经典中的经典算法:动态规划(详细解释,从入门到实践,逐步讲解)
每个动态规划都从一个网格开始。
在本题中，网格的各行表示商品，各列代表不同容量的背包（从1到V）。
网格最初是空的。你将填充其中的每个格子，网格填满后，就找到了问题的答案！
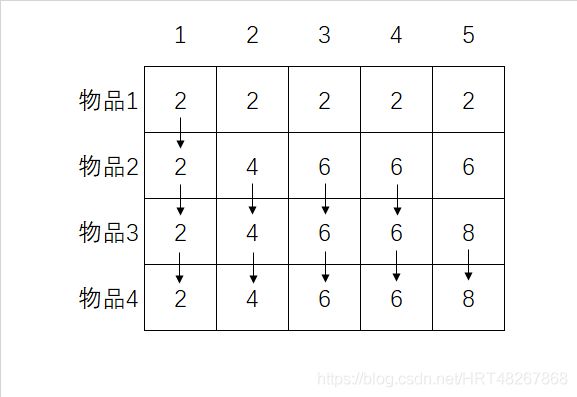
比如本题样例的网格如下图：

一、画好网格之后，先来看第一行。

在每个一格子你都要做出一个选择：放不放进这一行对应的物品。
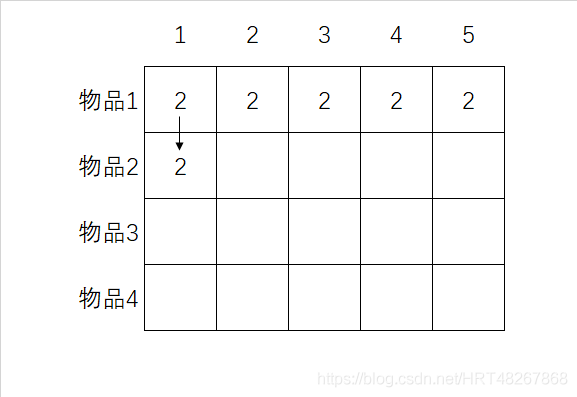
物品1所占空间为 $1$ ，也就是说物品1能放进容量为 $1$ 的这个背包，因此这个单元格包含物品1。所以往第一行第一列中装入物品1，价值为2。

这行的其他单元格也一样。别忘了，这是第一行，只有一个物品可供你选择，换而言之，你假装现在还没有打算放进其他物品。
填充完之后如下图：

此时你很可能心存疑惑：原题说的是容量为5的背包，我们为何要考虑容量为1、2、3、4的背包呢？**动态规划从子问题着手，逐步解决大问题。**这里解决的子问题将帮助你解决大问题。
**这行表示的是当前的最大价值，**并不是最终解。随着算法往下执行，将逐步修改最大价值。

二、接下来看第二行。

在第二行中，你有两种物品选择。先看第一个单元格，容量为1，之前装进去的最大的价值为2。
这一个单元格该不该放入第二个物品呢？答案显然是不行，因为容量为1的口袋无法装下占空间2的物品。
因此第一列的最大价值保持不变。

接下来看第二行第二列，这个格子所对应背包的容量为2，现在能够装下第二个物品了，对比一下价值，比之前决定的物品1价值高，所以将原来的物品1换为物品2。
再看后面的第三列，这个格子容量为3，可以同时装下物品1和物品2，所以都放进去。
之后的列也进行一样的操作，最后操作完第二行的结果为：

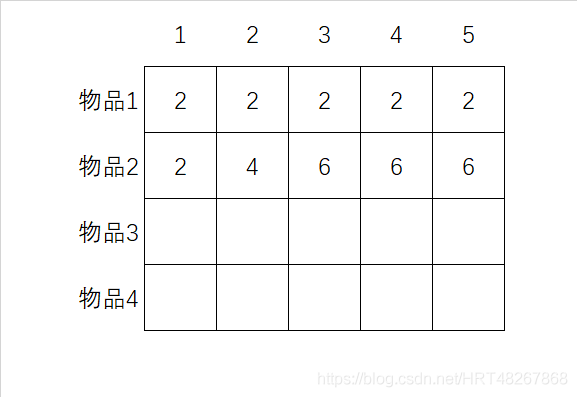
三、做完第二行，接下来看第三行

以同样的方式处理物品3，物品3占用空间3，价值为4。
其中在第五列时，容量为5，原本决定的为（物品1+物品2），现在有物品3可以选择了，所以考虑将物品1换为价值更高的物品3，所以此行第五列结果为8
做完这一步就得到了下面的网格：

四、第四行也一样

五、最终结果

可以总结得到一个公式：$$cell[i][j](i和j代指行和列)=两者中较大的一项\{\begin{array}{l}1.上一个单元格的值（即：cell[i-1][j]的值）\\ 2.当前物品的价值+剩余空间的价值（即：cell[i-1][j-当前物品的占用空间]+当前物品的价值）\end{array}$$
你可以使用这个公式来计算每个单元格的价值，最终的网格将与前一个网格相同。
这里回答前面抛出的问题：为什么要求解子问题？——因为你可以合并两个子问题的解来得到更大问题的解。
相信看到这里，并且亲手推导过网格，应该对动态规划的状态转移方程背后的逻辑有了更深的理解。现在，再回头看01背包问题的经典描述，并实现代码。

六、程序实现

声明一个数组dp[n+1][v+1]表示初始网格，首行为0，表示不放入任何物品，同时也为了代码阅读性，从下标1开始处理。

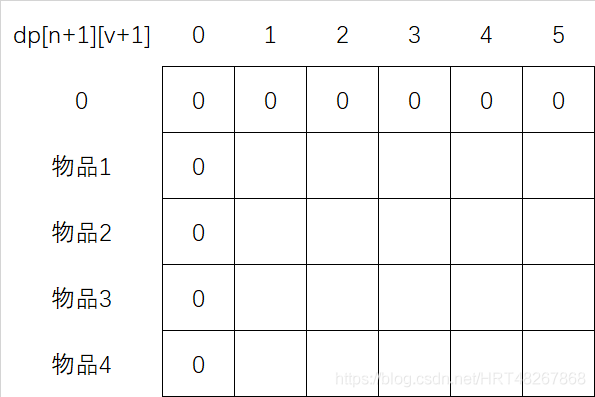
根据第五步的公式，对于编号为 $i$ 的物品：

• 如果将$i$放入，$当前背包的最大价值=第i号物品的价值+出去i号物品占用空间后剩余的空间所能存放的最大价值$。
  即：$valueWith\_i=w_i+dp[i-1][j-v_i];$
• 如果不放入$i$，$当前背包的价值=前i-1个物品存放在背包中的最大价值$。
  即：$valueWithout\_i=dp[i-1][j];$
• 最终，$dp[i][j]$的结果取两者的较大值。
  即：$dp[i][j]=Math.max(valueWith\_i,valueWithout\_i);$

解题代码2-Java

import java.util.*;

public class Main {
     
    static int maxValue(int n, int v, int[][] items) {
     
        if (n == 0) {
     
            return 0;
        }
        int[][] dp = new int[n + 1][v + 1];
        for (int i = 1; i <= n; i++) {
     
            for (int j = 1; j <= v; j++) {
     
                int valueWith_i = (j - items[i - 1][0] >= 0) ? (items[i - 1][1] + dp[i - 1][j - items[i - 1][0]]) : 0;
                int valueWithout_i = dp[i - 1][j];
                dp[i][j] = Math.max(valueWith_i, valueWithout_i);
            }
        }
        return dp[n][v];
    }

    public static void main(String[] args) {
     
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int v = input.nextInt();
        int totalV = 0, totalN = 0;
        int[][] items = new int[n][2];
        for (int i = 0; i < n; i++) {
     
            items[i][0] = input.nextInt();
            items[i][1] = input.nextInt();
            totalV += items[i][0];
            totalN += items[i][1];
        }
        input.close();
        if (totalV <= v) {
     
            System.out.println(totalN);
            return;
        }
        System.out.println(maxValue(n, v, items));
    }
}

解题代码3-Java：对于解题代码2的优化

import java.util.*;

public class Main {
     
    public static int N = 1010;

    public static void main(String[] args) {
     
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int v = input.nextInt();
        int[] dp = new int[N];
        for (int i = 1; i <= n; i++) {
     
            int vi = input.nextInt();
            int wi = input.nextInt();
            for (int j = v; j >= vi; j--) {
     
                dp[j] = Math.max(dp[j], dp[j - vi] + wi);
            }
        }
        System.out.println(dp[v]);
    }
}