A*算法（解决八数码问题）

A*算法简介

启发式搜索简介：

启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。

A*算法简介：

A*算法就是对估价函数加上一些限制后得到的一种启发式搜索算法。
其搜索过程可能描述如下：

1. 把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)；
2. 如果Open表为空，则问题无解，失败退出；
3. 把Open表的第一个节点取出放入Closed表，并记该节点为n；
4. 考察节点n是否为目标节点。若是，则找到了问题的解，成功退出；
5. 若节点n不可扩展，则转到第(2)步；
6. 扩展节点n，生成子节点n_i(i=1,2,……)，计算每一个子节点的估价值f(n_i) (i=1,2,……)，并为每一个子节点设置指向父节点的指针，然后将这些子节点放入Open表中；
7. 根据各节点的估价函数值，对Open表中的全部节点按从小到大的顺序重新进行排序；
8. 转第(2)步。

A*算法简单实现八数码问题

思路：

代码：

#include
#include
#include
#define MAX_NODESIZE 999999
#define N 3	//4



//----------------------------------八数码结构体----------------------------------//
typedef struct node
{
     
	//节点状态
	int a[N][N];

	//空格的下标
	int i_0, j_0;

	//启发信息
	int d, w, f;	//搜索深度，各棋子不在正确位置的数目，总代价

	//指向父节点指针
	struct node *father;
}node, *p_node;



//----------------------------------顺序表结构体----------------------------------//
typedef struct list
{
     
	p_node a[MAX_NODESIZE];
	long length;
}list, *p_list;



//-------------------------------初始节点&目标节点--------------------------------//
static int s0[N][N] = {
      2,8,3,1,0,4,7,6,5 };	//初始结点
//static int s0[N][N] = { 1,2,3,4,6,7,8,0,5,10,11,12,9,13,14,15 };
/*
2	8	3
1	0	4
7	6	5
*/

static int sg[N][N] = {
      1,2,3,8,0,4,7,6,5 };	//目标结点
//static int sg[N][N] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0 };
/*
1	2	3
8	0	4
7	6	5
*/


//---------------------------------结构体开辟空间---------------------------------//
p_node s_0 = (p_node)malloc(sizeof(node));		//初始节点
p_node s_g = (p_node)malloc(sizeof(node));		//目标节点

p_list OPEN = (p_list)malloc(sizeof(list));		//OPEN表
p_list CLOSE = (p_list)malloc(sizeof(list));	//CLOSE表



//------------------------------------声明函数------------------------------------//
int w(p_node s);						//启发函数，再次设置为曼哈顿距离
int f(p_node s);						//估价函数
void init_node();						//初始化
void out_node(p_node s);				//输出八数码
void list_reverse(p_node &p);			//将链表逆序
void out_list(p_list &l);				//输出OPEN表
bool search_list(p_list &l, p_node s);//对表进行查找，成功返回true
void sort_list(p_list &l);				//对OPEN表进行排序（按f从小到大）
void add_list(p_list &l, p_node s);	//加入结点到OPEN表中或CLOSE表中
void copy_node(p_node s1, p_node &s2);//生成新的结点（将s2赋值给s1）
void delete_list(p_list &l);			//从OPEN表或CLOSE中删除结点
bool is_equal(p_node s1, p_node s2);	//判断两节点是否相等
bool up_mov(p_node &s);				//空格上移
bool down_mov(p_node &s);				//空格下移
bool left_mov(p_node &s);				//空格左移
bool right_mov(p_node &s);				//空格右移
void move(p_node s);					//移动父节点并加入未探索表中（扩展结点）
int find_i(int a);
int find_j(int a);



//-------------------------------------主函数-------------------------------------//
int main()
{
     
	init_node();

	printf("\n程序求解过程如下：\n");
	printf("=================================================================\n\n");

	while (OPEN->length != 0 && CLOSE->length <= 1000)	//最多循环次数1000次
	{
     
		p_node n = OPEN->a[0];	//把Open表的第一个节点取出放入Close表，并记该节点为n
		delete_list(OPEN);

		if (is_equal(n, s_g))	//考察节点n是否为目标节点。若是，则找到了问题的解，成功退出；亦可换成 if(w(n)==0){...}
		{
     

			//out_node(n);
			list_reverse(n);
			list_reverse(n);
			list_reverse(n);
			while (n)
			{
     
				printf("第 %d 步：\n", n->d + 1);
				out_node(n);
				n = n->father;
			}

			break;
		}

		add_list(CLOSE, n);
		move(n);	//扩展节点

		sort_list(OPEN);
		out_list(OPEN);
	}

	if (OPEN->length == 0 || CLOSE->length > 10000)
	{
     
		printf("\n从初始结点无法到达目标结点！\n\n");
	}

	return 0;


}



//--------------------------计算启发函数，再次为曼哈顿距离---------------------------//
int w(p_node s)
{
     
	/*int r = 0;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			if (s->a[i][j] != sg[i][j])
				r++;
		}
	}
	if (s->a[1][1] == sg[1][1])
		r++;
	return r-1;*/
	int r = 0;
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			r += abs(i - find_i(s->a[i][j])) + abs(j - find_j(s->a[i][j]));
		}
	}
	return r;
}

int f(p_node s)
{
     
	return (s->d + s->w);
}


//-------------------------------------初始化-------------------------------------//
void init_node()
{
     
	//------------------------初始化初始节点

	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			s_0->a[i][j] = s0[i][j];

			if (s_0->a[i][j] == 0)
			{
     
				s_0->i_0 = i;
				s_0->j_0 = j;
			}
		}
	}

	s_0->d = 0;
	s_0->w = w(s_0);
	s_0->f = f(s_0);
	s_0->father = NULL;

	//------------------------初始化目标节点

	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			s_g->a[i][j] = sg[i][j];
			if (s_g->a[i][j] == 0)
			{
     
				s_g->i_0 = i;
				s_g->j_0 = j;
			}
		}
	}

	s_g->d = 0;
	s_g->w = w(s_g);
	s_g->f = f(s_g);

	OPEN->length = 0;
	CLOSE->length = 0;

	add_list(OPEN, s_0);	//初始节点加入OPEN表中

	printf("初始节点为：\n");	//打印初始节点
	out_node(s_0);

	printf("目标节点为：\n");	//打印目标节点
	out_node(s_g);
}



//---------------------------------输出八数码-------------------------------------//
void out_node(p_node s)
{
     
	printf("-------------------\n");
	//printf(" x=%d,y=%d\n", s->i_0, s->j_0);
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			printf("%5d", s->a[i][j]);
		}

		printf("\n");
	}
	printf("-------------------");
	printf(" d=%d,w=%d;  f=%d\n\n\n", s->d, s->w, s->f);
}



//---------------------------------将链表逆序-------------------------------------//
void list_reverse(p_node & p)
{
     
	p_node p_pre, p_suc;

	p_pre = NULL;
	p_suc = p->father;

	while (p)
	{
     
		p->father = p_pre;
		p_pre = p;
		if (p_suc == NULL)
			break;
		p = p_suc;
		p_suc = p_suc->father;
	}
}



//---------------------------------输出OPEN表-------------------------------------//
void out_list(p_list &l)
{
     
	printf("****************************************************************\n");
	for (int i = 0; i < l->length; i++)
	{
     
		out_node(l->a[i]);
	}
	printf("****************************************************************\n");
}


//-------------------------对表进行查找，成功返回true-----------------------------//
bool search_list(p_list &l, p_node s)
{
     
	for (int i = 0; i < l->length; i++)
	{
     
		if (is_equal(l->a[i], s))
			return true;
	}

	return false;
}



//-------------------对OPEN表进行排序（按f从小到大）(插入）-----------------------//
void sort_list(p_list &l)
{
     
	p_node temp = (p_node)malloc(sizeof(node));

	for (int i = 1; i < l->length; i++)
	{
     
		int j = i - 1;
		copy_node(temp, l->a[i]);
		while (j >= 0 && (temp->f < l->a[j]->f))
		{
     
			copy_node(l->a[j + 1], l->a[j]);//l->a[j + 1] = l->a[j];
			j--;
		}
		copy_node(l->a[j + 1], temp);
	}
}


//------------------------加入结点到OPEN表中或CLOSE表中---------------------------//
void add_list(p_list & l, p_node s)
{
     
	l->a[l->length++] = s;
}


???
//-------------------------生成新的结点（将s2赋值给s1）---------------------------//
void copy_node(p_node s1, p_node &s2)
{
     
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			s1->a[i][j] = s2->a[i][j];
		}
	}

	s1->i_0 = s2->i_0;
	s1->j_0 = s2->j_0;

	s1->d = s2->d;
	s1->w = s2->w;
	s1->f = s2->f;
	s1->father = s2->father;
}



//--------------------------从OPEN表或CLOSE中删除结点-----------------------------//
void delete_list(p_list & l)
{
     
	for (int i = 0; i < l->length; i++)
	{
     
		l->a[i] = l->a[i + 1];
	}
	l->length--;
}



//----------------------------判断两节点是否相等----------------------------------//
bool is_equal(p_node s1, p_node s2)
{
     
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			if (s1->a[i][j] != s2->a[i][j])
			{
     
				return false;
			}
		}
	}

	return true;
}



//----------------------------------空格左移--------------------------------------//
bool left_mov(p_node &s)
{
     
	if (s->j_0 == 0)
		return false;
	int temp;
	temp = s->a[s->i_0][s->j_0];
	s->a[s->i_0][s->j_0] = s->a[s->i_0][s->j_0 - 1];
	s->a[s->i_0][s->j_0 - 1] = temp;

	s->j_0--;
	return true;
}



//----------------------------------空格右移--------------------------------------//
bool right_mov(p_node &s)
{
     
	if (s->j_0 == N - 1)
		return false;

	int temp;
	temp = s->a[s->i_0][s->j_0];
	s->a[s->i_0][s->j_0] = s->a[s->i_0][s->j_0 + 1];
	s->a[s->i_0][s->j_0 + 1] = temp;

	s->j_0++;
	return true;
}



//----------------------------------空格上移--------------------------------------//
bool up_mov(p_node &s)
{
     
	if (s->i_0 == 0)
		return false;

	int temp;
	temp = s->a[s->i_0][s->j_0];
	s->a[s->i_0][s->j_0] = s->a[s->i_0 - 1][s->j_0];
	s->a[s->i_0 - 1][s->j_0] = temp;

	s->i_0--;
	return true;
}



//----------------------------------空格上移--------------------------------------//
bool down_mov(p_node &s)
{
     
	if (s->i_0 == N - 1)
		return false;

	int temp;
	temp = s->a[s->i_0][s->j_0];
	s->a[s->i_0][s->j_0] = s->a[s->i_0 + 1][s->j_0];
	s->a[s->i_0 + 1][s->j_0] = temp;

	s->i_0++;
	return true;
}



//----------------------移动父节点并加入未探索表中（扩展结点）--------------------//
void move(p_node s)
{
     
	p_node p1 = (p_node)malloc(sizeof(node));
	p_node p2 = (p_node)malloc(sizeof(node));
	p_node p3 = (p_node)malloc(sizeof(node));
	p_node p4 = (p_node)malloc(sizeof(node));

	copy_node(p1, s);
	copy_node(p2, s);
	copy_node(p3, s);
	copy_node(p4, s);

	p1->father = s;
	p2->father = s;
	p3->father = s;
	p4->father = s;

	//如果能够移动且在CLOSE表中不存在，则加入OPEN表中
	if (left_mov(p1) && !is_equal(p1, p1->father) && !search_list(CLOSE, p1) && !search_list(OPEN, p1))
	{
     
		add_list(OPEN, p1);
		p1->d++;
		p1->w = w(p1);
		p1->f = f(p1);
	}
	else
		free(p1);

	if (right_mov(p2) && !is_equal(p2, p2->father) && !search_list(CLOSE, p2) && !search_list(OPEN, p2))
	{
     
		add_list(OPEN, p2);
		p2->d++;
		p2->w = w(p2);
		p2->f = f(p2);
	}
	else
		free(p2);

	if (up_mov(p3) && !is_equal(p3, p3->father) && !search_list(CLOSE, p3) && !search_list(OPEN, p3))
	{
     
		add_list(OPEN, p3);
		p3->d++;
		p3->w = w(p3);
		p3->f = f(p3);
	}
	else
		free(p3);

	if (down_mov(p4) && !is_equal(p4, p4->father) && !search_list(CLOSE, p4) && !search_list(OPEN, p4))
	{
     
		add_list(OPEN, p4);
		p4->d++;
		p4->w = w(p4);
		p4->f = f(p4);
	}
	else
		free(p4);
}

int find_i(int a)
{
     
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			if (sg[i][j] == a)
				return i;
		}
	}
}

int find_j(int a)
{
     
	for (int i = 0; i < N; i++)
	{
     
		for (int j = 0; j < N; j++)
		{
     
			if (sg[i][j] == a)
				return j;
		}
	}
}

可以设置N为4，计算15数码问题

#define N 4
static int s0[N][N] = {
      1,2,3,4,6,7,8,0,5,10,11,12,9,13,14,15 };	//初始结点
static int sg[N][N] = {
      1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0 };	//目标结点

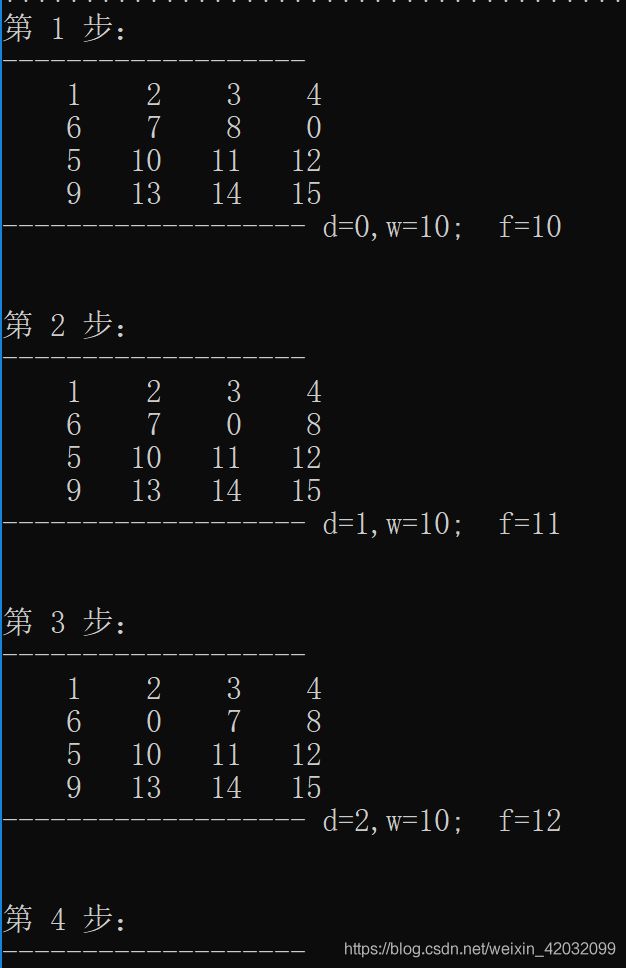
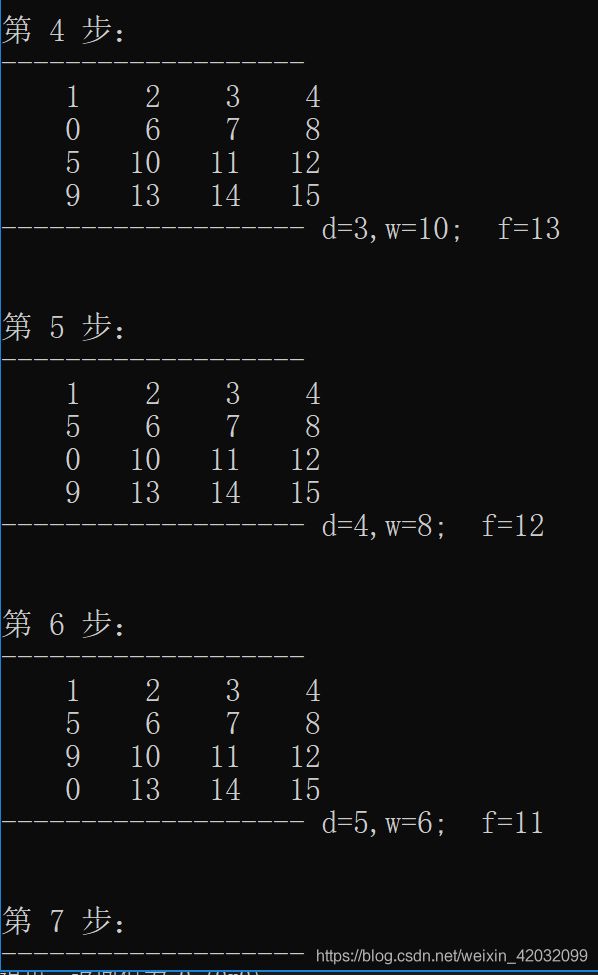
此时的运行结果为：