Zero-Shot Learning论文学习笔记（第三周）

Feature Generating Networks for Zero-Shot Learning

原文链接：

http://openaccess.thecvf.com/content_cvpr_2018/papers/Xian_Feature_Generating_Networks_CVPR_2018_paper.pdf

摘要

深度学习经常被用于计算机视觉任务中，但是深度学习需要大量的训练数据，然而实际情况中常常缺乏这些数据,这也就造成了seen class和unseen class训练数据大多数情况下的极度不平衡。

GAN网络可以生成很真实且清晰的图像，但是由于这种图像类别间的不平衡，现有的ZSL方法在GZSL任务上的性能很差。

文章提出基于GAN框架，利用语义信息来生成不可见类的CNN特征。文章的方法利用Wasserstein GAN和分类损失，生成判别性强的CNN特征，来训练分类器。作者的实验结果表明，在零样本学习和广义零样本学习设置中，在五个具有挑战性的数据集（CUB，FLO，SUN，AWA和ImageNet）上的准确率比其他方法有显著提高。

由下图所示，CNN的特征可以从以下几个方面提取：
1）真实图像，但是在零次学习中，无法获得任何不可见类的真实图像；
2）合成图像，但是它们不够精确，无法提高图像分类性能。
文章为了解决了这两个问题，提出了一种新的基于属性条件特征生成对抗性网络公式，即f-CLSWGAN，用于生成不可见类的cnn特征。
论文提出了两个任务，zero shot learning (ZSL)和generalized zero shot learning（GZSL），前者只需要解决未见过的数据的分类任务，后者需要同时对见过的和未见过的数据进行分类。

算法简介：

使用GAN在特征空间生成数据的原因

文章提到了DC-GAN，InfoGAN和Wasserstein-GAN（WGAN），指出这些先进的GAN虽然已经可以生成逼真的图像，但是并没有将这一思想应用到图像特征生成中的先例。
（1）生成的特征数据是无限制的。
（2）生成的特征通过大规模数据集学习到的具有代表性的特征表示，可以在某种程度上泛化未知类别的特征。
（3）学习的特征具有很强的判别性。

• 作者使用三种conditional GAN的变体来循序渐进的生成图像特征：embedding feature。

1. 首先通过下式表示可见类和不可见类。
   $$S=\{(x,y,c(y))|x\in X,y\in Y^s,c(y)\in C\}$$
   $$U=\{(u,c(u))|u\in Y^u,c(u)\in C\}$$
   其中$S$代表可见训练集全体，$x\in R^{d_x}$是CNN特征，$y^s=\{y_1,...,y_k\}$代表有$k$个不交叉的可见类，$y$代表类标签，$c(y)\in R^{d_c}$代表y类的embedding 属性集，由语义向量构成。
   U代表不可见类，与可见类相比，缺少了图像和图像特征，也就缺少了CNN特征。
2. 在给出S和U的类别定义后，文章给出ZSL和GZSL的任务要求：
   ZSL的任务：学习一个分类器$f_{zsl}:X\to Y^u$;
   GZSL的任务：学习一个分类器$f_{gzsl}:X\to Y^s\cup Y^u$。

1.f-GAN

• f-GAN的目标是学习一个条件生成器$G:Z\times C\to X$
  其中Z是从高斯分布中随机采样的噪声$z\in Z\subset R^{d_z}$，$c(y)\in C$是类别$y$的语义向量，这两者作为输入。$\hat{x}\in X$是$y$类中的CNN feature,作为输出。

1.1 original-GAN

• 传统的GAN网络的损失函数如下：
  $${\min }_G{\max }_{D}GAN=E_{x\sim P_{\text{ data }}}[\log D(x)]+E_{z\sim P_z}[\log (1-D(G(z)))]$$
  算法&训练步骤如下图所示。

1. distribution 可以是Gaussian distribution或Uniform distribution等等
2. generated data $\hat{x}$为生成的图片
3. 分类器$D$的最后一层为Sigmoid，保证生成的值在0～1之间
4. 因为要让$\hat{V}$越大越好，所以采用gradient ascent方法更新判别器$D$的参数${\theta }_d$
5. Lerning D 和Learning G过程中的random vectors 可以不同

1.2.conditional-GAN

conditional-GAN的大致训练过程如下图所示。与传统的GAN相比，conditional-GAN的$G$在接受一个distribution$z$的同时还接受一个文本描述（语义）$c$，$D$在接受$G$生成的图片$x$同时接受文本描述$c$,$x$的真实度和$c$与$x$匹配程度

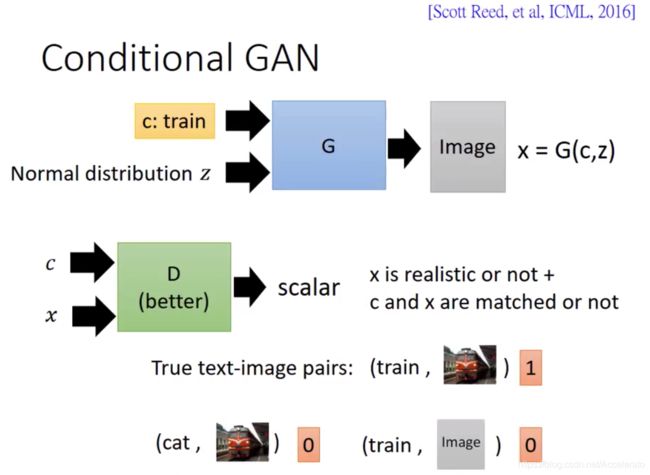
在 conditonal-GAN中$D$和$G$的学习步骤如下所示。

1.3.f-GAN

• f-GAN的损失函数如下：

$$\begin{array}{l}{\min }_G{\max }_D{L}_{GAN}=E[\log D(x,c(y))]+E[\log (1-D(\tilde{x},c(y)))]\end{array}$$
其中$\hat{x}=G(z,c(y))$,$c(y)$是类别$y$的语义向量。判别器$D:X\times C\to [0,1]$的最后一层是Sigmoid函数。$D$试图最大化$loss$，而生成器$G$试图最小化$loss$。因为 $\tilde{x}$和$c(y)$属于相同类，所以在loss function中不需要考虑不匹配的问题。

• 文章指出了f-GAN的不足之处：虽然GAN能够捕获复杂的数据分布(比如生成图片)，但它的训练过程很困难。

2.f-WGAN

2.1.Wasserstein GAN

在original-GAN中衡量的是generated data和real-data之间的JS divergence。但由于两者的distribution往往没有任何重叠，下图给出了没有重叠的两个原因。

1. $P_G$和$P_{d}ata$的支撑集是高维空间中的低维流形。
2. 如果没有足够多的样本， $P_G$和$P_{d}ata$即使重叠概率也很低。
   
   可以证明，当$P_G$和$P_{d}ata$不重叠时两者的JS divergence 是$log2$
   为了解决这个问题，2017的Wasserstein GAN的paper中提出了Wasserstein distance的概念，Wasserstein distance又被称为Earth-Mover（EM）距离，直观解释图如下所示。
   
   判别器$D$通过下式训练得到的目标函数值就是Wasserstein distance。
   $${\max }_{D\in 1-Lipschitz}\{E_{x\sim P_{data}}[D(x)]-E_{x\sim P_G}[D(x)]\}$$
   可见，如果$x$来自$P_{data}$，那么$D$的output越大越好，如果来自$P_G$,那么越小越好。同时，$D$必须是一个$1-Lipschitz$ 函数，$Lipschitz$函数定义如下所示。
   $$|f(x_1)-f(x_2)|\le K|x_1-x_2|$$
   这里不等式左边可以理解为为ouput的变化量，右边为input的变化量，所以$Lipschitz$ 函数限制了input变化时output的变化范围，当$K$为1时就是$1-Lipschitz$ 的形式。此时output的变化总是小于input的变化，也就保证了生成器$D$的平滑。

2.2. f-WGAN

• 通过将生成器$G$和判别器$D$的语义属性混合文章把著名的Wasserstein GAN拓展为conditional WGAN。损失函数如下所示。
  $$\begin{array}{l}{\min }_G{\max }_D{L}_{WGAN}=E[D(x,c(y))]-E[D(\tilde{x},c(y))]-\lambda E[(\Vert {\nabla }_{\hat{x}}D(\hat{x},c(y)){\Vert }_2-1{)}^2]\end{array}$$其中$\tilde{x}=G(z,c(y))$、$\hat{x}=\alpha x+(1-\alpha )\tilde{x}$、$\alpha \sim U(0,1)$、 $\lambda$ 是处罚系数。

• 式子中的前两项是在近似Wasserstein distance，第三项是梯度惩罚项(gradient penalty)，使得判别器D的梯度在1附近。

3.f-CLSWGAN

作者认为单纯使用WGAN还不足以使generator生成的features能够训练出一个好的分类器，所以作者提出分类损失并用采用负对数的形式刻画。
$$L_{CLS}=-E_{\tilde{x}\sim p_{\tilde{x}}}[\log P(y|\tilde{x};\theta )]$$
其中$\hat{x}=G(z,c(y))$。分类器采用线性softmax分类器， $P(y|\tilde{x};\theta )$表示$\tilde{x}$被类别标签$y$真实预测的概率。 分类器的参数θ是根据可见类的实际特征进行预训练的。

该分类损失可以看作是正则化项，迫使生成器构造判别性强的特征。
最终的损失函数如下所示，其中$\beta$ 是一个超参数权重。
$${\min }_G{\max }_D{L}_{WGAN}+\beta L_{CLS}$$

4. Discriminator的架构

下图为Conditional GAN中两种经典的架构方式，当输出的score取低分时，第一种架构没有办法判断低分的原因是$x$不够真实清晰还是与类别标签$c$不匹配，第二个模型由于分别输出两个网络的socre，所以可以解决上述问题。

论文模型如下图所示，与上图的模型二类似。
图中第一行是真实图像的特征提取过程，里面的CNN可以通过用的GoogleNet或ResNet，可以是从ImageNet上预训练的模型，也可以是在特定任务中微调过的模型，本文中采用的预训练模型。将特征$x$与$x$所属类的属性描述$c(y)$拼接后输入Discriminator并判别为真；

图中第二行是生成数据的分支，用normal distribution的$z$与$c(y)$拼接后输入生成器，生成特征xˆ再次将其与属性描述拼接后输入Discriminator并判别为假；同时输出$P(y|\tilde{x};\theta )$的值观察Generator构造的特征性的强弱。

实验

1.f-CLSWGAN模型在ZSL和GZSL任务上的性能。

数据集简介

1）Caltech-UCSD-Birds 200-2011 (CUB)包含来自200个鸟类的11788幅图片，并且带有312个属性描述，如图一中显示的头和腹部的颜色、鸟喙的形状等；
2）Ox- ford Flowers (FLO) 包含来自102类花的8189幅图片，没有属性描述；
3）SUN Attribute (SUN) 包含来自717个场景下的14340幅图片，并带有102个属性描述；
4）Animals with Attributes (AWA)包含来自50个动物类的30475幅图片，带有85个属性。

关于准确率

论文使用top-1准确率评估如下三个项目：见到过的类别分类$s$，未见到过的类别分类$u$,二者的调和平均数$H,H=\frac{2(s\ast u)}{(s+u)}$。

• Top-1 Accuracy：假设ImageNet有1000个分类，模型预测某张图片时，会给出1000个按概率从高到低的类别排名，Top-1 Accuracy是指排名第一的类别与实际结果相符的准确率。
• 调和平均数：$$H_n=\frac{1}{\frac{1}{n}{\sum }_{i=1}^n\frac{1}{x_i}}=\frac{n}{{\sum }_{i=1}^n\frac{1}{x_i}}$$

• ZSL方面：将f-CLSWGAN模型应用到DEVISE等方法后，性能都有所提升，验证了 f-CLSWGAN能够为unseen class生成有效的视觉特征；其中在算法ALE的基础上得到了the-state-of-the-art的表现。
• GZSL方面：使用 f-CLSWGAN模型后性能提升，验证了该方法的有效性。此外，我们观察到，在使用f-CLSWGAN前，seen class的准确率显著高于unseen class，说明很多图像被错误地判别为seen class。而f-CLSWGAN模型在$s$和$u$之间取得了一个平衡，尽管$s$相比baseline有所下降，但是$s$有大幅上升，直接导致了$H$的上升。
• 另外，借助f-CLSWGAN模型，仅使用最简单softmax分类器就已经可以达到很好的效果，甚至部分情况下性能已经超过其他模型，在GZSL上取得了the-state-of-the-art的性能，表明了说明论文提出的方法对于未见过的数据生成非常有效，也说明了基于特征生成的思想在其他任务上也具有泛化能力。

f-xGAN各种变体在ZSL和GZSL任务上的性能

1、在ZSL和GZSL场景下，f-xGAN模型都能够提升性能，在GZSL任务上更是显著提升；
2、文章中最后提出的f-CLSWGAN模型在生成模型中性能最好；
3、即使f-WGAN比f-GMMN表现差（在FLO数据集GSZL方法上），f-CLSWGAN模型也能够借助分类损失达到最佳性能。

不同条件下分析f-xGAN各种变体

稳定性测试：首先分析不同的生成模型拟合seen class的能力。生成seen class的CNN特征，再训练softmax分类器。黑色虚线是在真实图像上的准确率，与之相比，f-GAN模型欠拟合，其他模型性能很好，说明f-xGAN模型训练稳定而且能生成有效的特征。

泛化性测试：使用预先训练的模型训练unseen class的cnn特征。再把这些cnn特征和 seen classes的真实CNN特征输入softmax分类器，下图显示了在unseen class中生成特征数量的增加将会显著提高预测准确性。

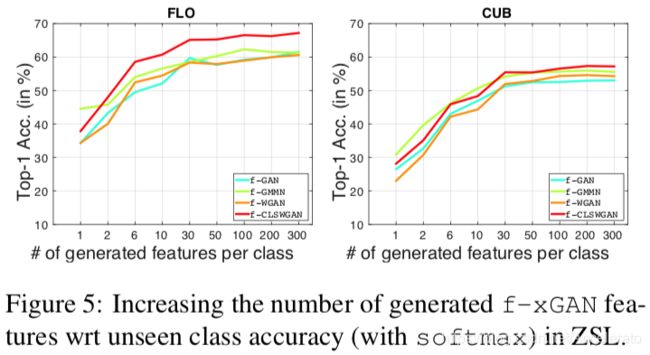
f-CLSWGAN在不同CNN网络结构下的表现情况

由实验结果可知，ResNet的总体性能要优于GoogleNet；且对于这两种CNN结构，使用f-xGAN模型后性能都有提升，验证了f-xGAN模型适用于不同的CNN结构。

Yongqin Xian, Tobias Lorenz, Bernt Schiele, Zeynep Akata. “Feature Generating Networks for Zero-Shot Learning.” CVPR (2018)
Arjovsky M , Chintala S , Bottou, Léon. Wasserstein GAN[J]. 2017.
https://zhuanlan.zhihu.com/p/25071913
https://youtu.be/3JP-xuBJsyc