Matlab的plot函数、fplot函数

plot函数

1. plot(x,y)
x和y分别表示用于存储x坐标和y坐标的数据。

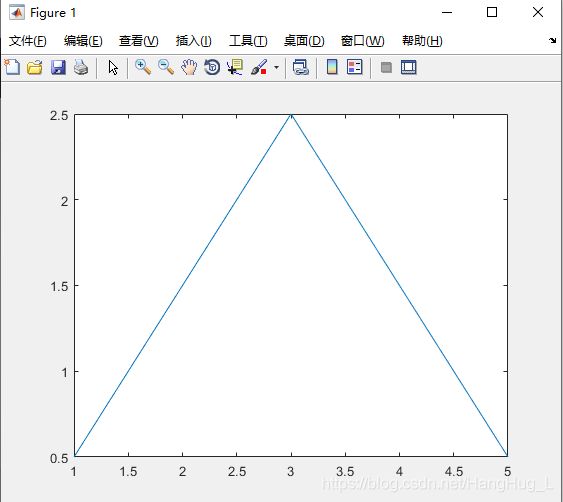
>> x=[1:5];
>> y=[0.5,1.5,2.5,1.5,0.5];
>> plot(x,y)

2. plot(x)

• 当x为实数时，以该向量元素的下标为横坐标，该向量的值为纵坐标绘制曲线。

所以1中的例子也可以简化为如下，画出的图像是一样的。

>> x=[0.5,1.5,2.5,1.5,0.5];
>> plot(x)

• 当x为虚数(复数向量)，分别以该向量元素实部和虚部为横、纵坐标绘制曲线。

>> x=[1:5];
>> y=[0.5,1.5,2.5,1.5,0.5];
>> r=x+y*i;  //都是字母这种情况下必须要有 乘* 
>> plot(r)

除了用r=x+y*i;获得复数r，还可以用complex函数。

>> x=[1:3];
>> y=[4:6];
>> r=complex(x,y)    //等同于r=x+y*i
r =
   1.0000 + 4.0000i   2.0000 + 5.0000i   3.0000 + 6.0000i

3. plot的参数x，y一般为长度相等的向量，但是也可以是矩阵。

• 当x为向量，y为矩阵时

1.如果矩阵y的列数等于x的长度，则以向量x为横坐标，以矩阵y的每 个行向量为纵坐标绘制曲线，曲线的条数等于y的行数。
2.如果矩阵y的行数等于x的长度，则以向量x为横坐标，以矩阵y的每个列向量为纵坐标绘制曲线，曲线的条数等于y的列数。
3.当矩阵y的行数等于列数，等于x的长度时，以第二种情况为标准：每个列向量做纵坐标。

>> x=[1:5];
>> y=[1:5;3:7;5:9;7:11;9:13]
y =
     1     2     3     4     5
     3     4     5     6     7
     5     6     7     8     9
     7     8     9    10    11
     9    10    11    12    13
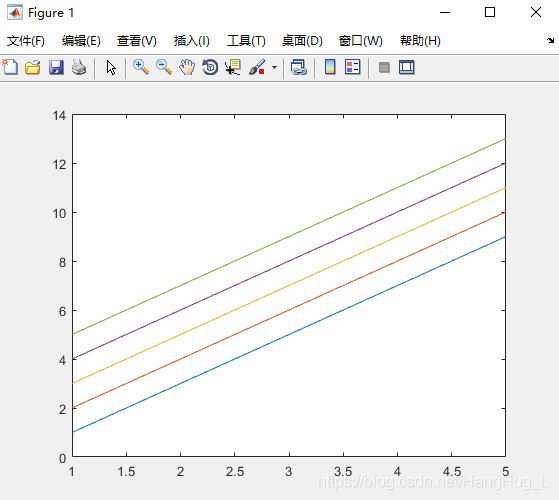
>> plot(x,y)

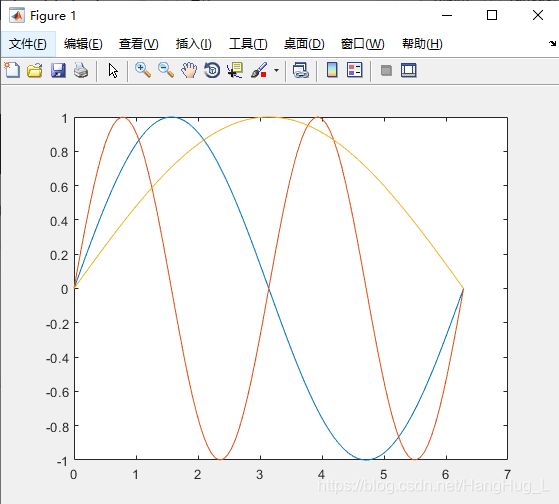
例1：绘制sin(x)，sin(2x)，sin(x/2) 的函数曲线。

>> x=linspace(0,2*pi,100);
>> y=[sin(x);sin(2*x);sin(0.5*x)];
>> plot(x,y)    //这就是矩阵y的列数等于x的长度的情况，且y的行数为3，所以有3条曲线

　

linspace函数：linspace(a,b,N);生成a到b之间的等间距的数组，该数组有N个元素，即N等分。
默认N是100，那么可以省略N。

>> x=linspace(1,5,5)
x =
     1     2     3     4     5
此时linspace的作用相当于x=[1:1:5];或者x=[1:5];

• 当x、y是同型矩阵时

以x、y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。

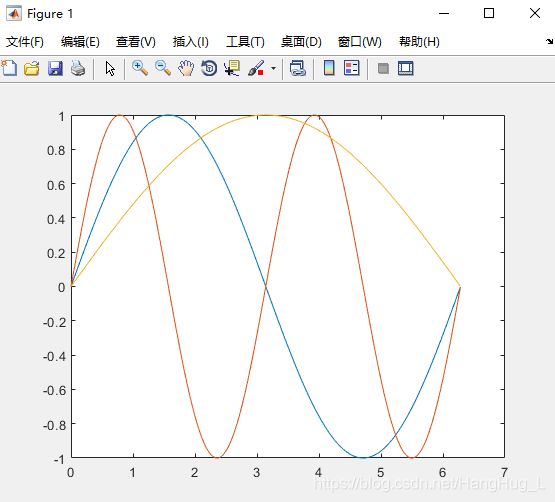
接上面的例1，这次用N行3列的方式绘出图像(前面是用3行100列)

>> t=0:0.01:2*pi;
>> t1=t.';     //矩阵t进行转置
>> x=[t1,t1,t1];
>> y=[sin(t1),sin(2*t1),sin(0.5*t1)];
>> plot(x,y)

　

4. 含多个输入参数的plot函数
plot(x₁,y₁,x₂,y₂,……,x_n,y_n,)
其中，每一 向量对 构成一组 数据点 的横、纵坐标，并绘制一条曲线。
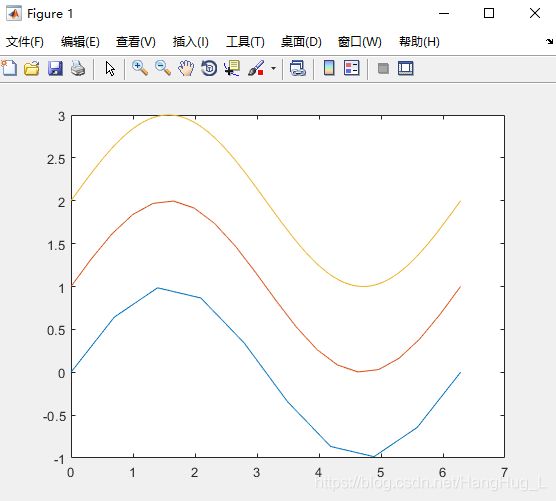
例2：采用不同个数的数据点绘制正弦函数曲线，观察曲线形态。
结论：所取的点越多，曲线越光滑。

>> t1=linspace(0,2*pi,10);
>> t2=linspace(0,2*pi,20);
>> t3=linspace(0,2*pi,100);
>> plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2)

5. 含选项的plot函数
　plot(x,y,选项)

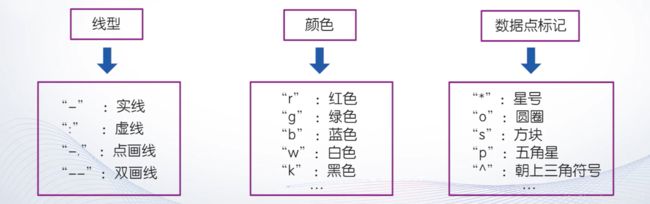
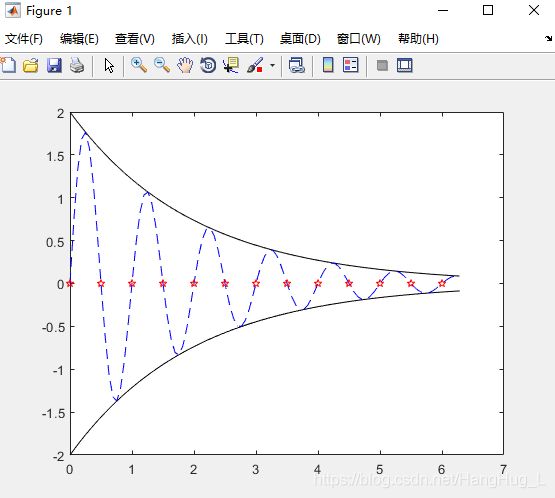
例3：用不同线型和颜色在同一坐标内绘制曲线y=2e^-0.5xsin(2πx)及其包络线。

>> x=(0:pi/50:2*pi).';        //直接一步实现转置
>> y1=2*exp(-0.5*x)*[1,-1];   //画出包络线
>> y2=2*exp(-0.5*x).*sin(2*pi*x);
>> x1=0:0.5:6;
>> y3=2*exp(-0.5*x1).*sin(2*pi*x1);
>> plot(x,y1,'k',x,y2,'b--',x1,y3,'rp')

得到一维矩阵好像有3种形式都对，
x=0:0.5:6
x=(0:0.5:6)
x=[0:0.5:6]
不过上面用到就是第一种，可能是这种步长得到矩阵不需要用方括号吧，如果是已知数据的初始化就需要方括号，而小括号多是和函数挂钩的。

fplot函数

对于一些函数，如果仍采取等间隔取样，则不能正确描绘出函数图像。比如sin(1/x)是一条变频率的震荡曲线，越接近原点频率越大，在0附近无穷震荡。

>> x=0:0.005:0.2;
>> y=sin(1./x);
>> plot(x,y)

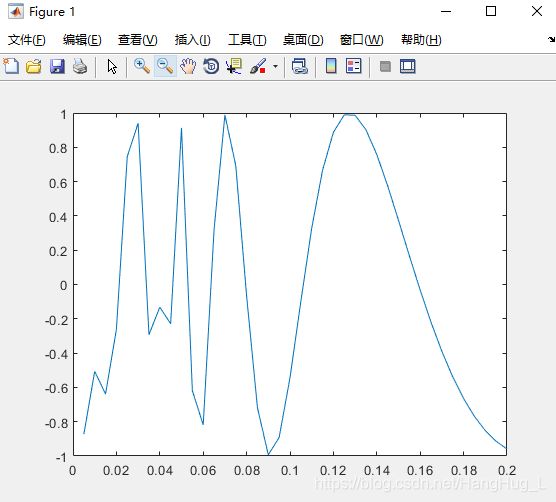
而绘制的曲线不能正确反映，使用fplot函数可根据参数函数的变化特性自适应的设置间隔。

• 格式：fplot(f,lims,选项)

其中，f代表一个函数，通常采用函数句柄的形式。lims为x轴的取值范围，用二元向量**[xmin，xmax]**描述，默认值为[-5，5]。选项定义与plot函数相同。

>> f=@(x) sin(1./x); 
>> fplot(f,[0,0.2])

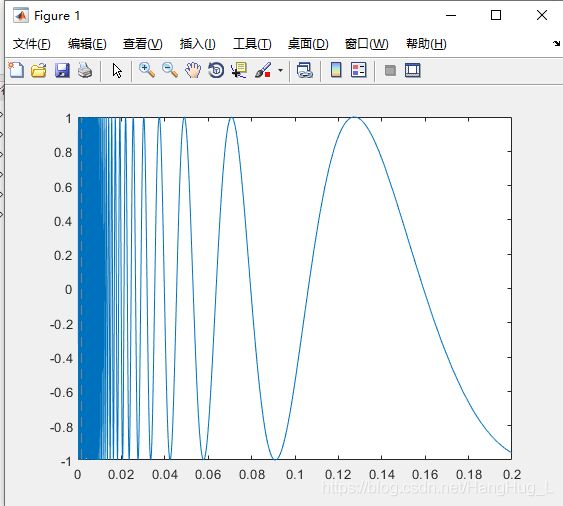
• 双输入函数参数：fplot(funx，funy，tlims，选项)

其中，funx、funy代表函数，通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围，(这要求funx和funy是同一个自变量)，用二元向量**[tmin，tmax]**描述，默认是[-5，5]。

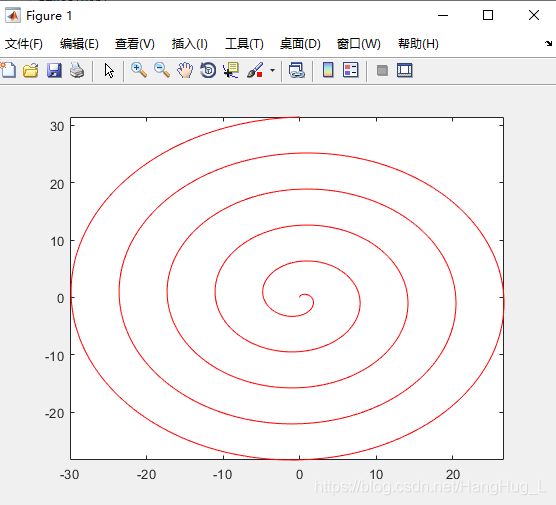
>> fplot(@(t) t.*sin(t),@(t) t.*cos(t),[0,10*pi],'r')