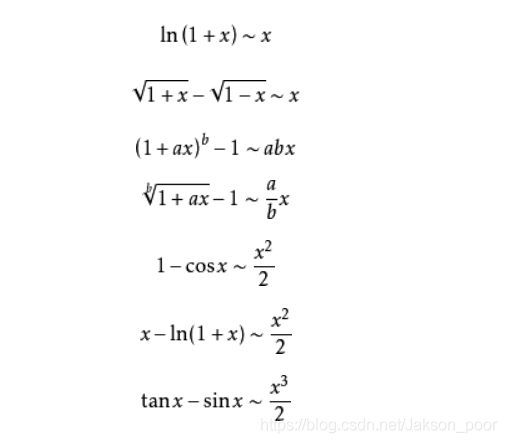高等数学期末总复习 DAY 1. 求极限 判断函数连续性
求极限
- 利用四则运算求极限
- 利用等差、等比数列的性质求极限
- 抓大头求极限
- 分子分母有理化求极限
- 一个重要结论
- 重要极限
- 夹逼定理的应用
- 等价无穷小的代换
1.利用四则运算求极限
例题1.
lim x → 1 ( 1 1 − x − 3 1 − x 3 ) \lim_{x \to 1}(\frac {1} {1-x} - \frac{3}{1-x^3} ) limx→1(1−x1−1−x33)
解:先进行四则运算后进行通分运算
原式:
= lim x → 1 ( 1 1 − x − 3 ( 1 − x ) ( 1 + x + x 2 ) ) \lim_{x\to 1}(\frac{1}{1-x} - \frac{3}{(1-x)(1+x+x^2)}) limx→1(1−x1−(1−x)(1+x+x2)3)
= lim x → 1 ( 1 + x + x 2 ) − 3 ( 1 − x ) ( 1 + x + x 2 ) \lim_{x\to 1}\frac{(1+x+x^2) -3}{(1-x)(1+x+x^2)} limx→1(1−x)(1+x+x2)(1+x+x2)−3
= lim x → 1 ( x + 2 ) − ( x − 1 ) ( 1 − x ) ( 1 + x + x 2 ) \lim_{x\to 1}\frac{(x+2) -(x-1)}{(1-x)(1+x+x^2)} limx→1(1−x)(1+x+x2)(x+2)−(x−1)
= − lim x → 1 x + 2 1 + x + x 2 -\lim_{x\to 1}\frac{x+2}{1+x+x^2} −limx→11+x+x2x+2
= -1
2.利用等差、等比数列的性质求极限
等差、等比数列的性质
| 数列 | 性质 |
|---|---|
| 等差 | |
| a n a_n an = a 1 a_1 a1+ (n-1)d | 第an项 |
| S n S_n Sn = n a 1 a_1 a1 + n ( n − 1 ) d 2 \frac{n(n-1)d}{2} 2n(n−1)d 或者 n ( a 1 + a n ) 2 \frac{n(a_1 +a_n)}{2} 2n(a1+an) | 前n项和 |
| 等比 | |
| b n b_n bn = b 1 q n − 1 b_1q^{n-1} b1qn−1 | 第n项 |
| S n S_n Sn = b 1 ( 1 − q n ) 1 − q \frac{b_1(1-q^{n})}{1-q} 1−qb1(1−qn) | 前n项和 |
例2
lim n → ∞ 1 + 2 + . . . + ( n − 2 ) n 2 \lim_{n\to \infty}\frac{1+2+...+(n-2)}{n^2} limn→∞n21+2+...+(n−2)
解:
原式:
= lim n → ∞ ( n − 2 ) ( n − 1 ) 2 n 2 \lim_{n\to \infty}\frac{\frac{(n-2)(n-1)}{2}}{n^2} limn→∞n22(n−2)(n−1)
= lim n → ∞ n 2 − 3 n + 2 2 n 2 \lim_{n \to \infty}\frac{n^2-3n+2}{2n^2} limn→∞2n2n2−3n+2
= lim n → ∞ 2 n 2 − 3 n + 1 2 \lim_{n \to \infty}\frac{\frac{2}{n^2}-\frac{3}{n}+1}{2} limn→∞2n22−n3+1
= 1 2 \frac{1}{2} 21
3.抓大头求极限
注:抓大头就是抓极限变化速度快的那一项
例3
lim n → ∞ ( n + 1 ) ( n + 2 ) ( n + 3 ) 5 n 3 \lim_{n \to \infty} \frac{(n+1)(n+2)(n+3)}{5n^3} limn→∞5n3(n+1)(n+2)(n+3)
在这道例题中明显分母的变化速度快于分子
解:原式
= lim n → ∞ 1 + C n 2 n 3 + C n n 3 + C n 3 5 \lim_{n \to \infty} \frac{1+\frac{Cn^2}{n^3}+\frac{Cn}{n^3}+\frac{C}{n^3}}{5} limn→∞51+n3Cn2+n3Cn+n3C
其中C为式中未计算的一常数
= 1 5 \frac{1}{5} 51
4.分子分母有理化求极限
例4
lim x → 1 \lim_{x \to 1} limx→1 5 x − 4 − x x − 1 \frac{\sqrt{5x-4}-\sqrt{x}}{x-1} x−15x−4−x
解:原式
= lim x → 1 ( 5 x − 4 − x ) + ( 5 x − 4 + x ) ( x − 1 ) 5 x − 4 + x \lim_{x \to 1} \frac{(\sqrt{5x-4}-\sqrt{x})+(\sqrt{5x-4}+\sqrt{x})}{(x-1)\sqrt{5x-4}+\sqrt{x}} limx→1(x−1)5x−4+x(5x−4−x)+(5x−4+x)
= lim x → 1 4 5 x − 4 + x \lim_{x\to 1}\frac{4}{\sqrt{5x-4}+\sqrt{x}} limx→15x−4+x4
= 2
5.一个重要结论
有界函数 x 无穷小量 = 0
其中常见的有界函数有:
sinx 、tanx、arcsinx、arctanx、
常见无穷小量有:
lim x → 0 x \lim_{x\to 0}x limx→0x
lim x → ∞ 1 x \lim_{x\to \infty}\frac{1}{x} limx→∞x1
例5
- lim x → 0 x ∗ sin 1 x \lim_{x\to 0}x*\sin{\frac{1}{x}} limx→0x∗sinx1 = 0 其中 sin 1 x \sin{\frac{1}{x}} sinx1为有界函数,而 lim x → 0 x \lim_{x\to 0}x limx→0x 为无穷小量
- lim x → ∞ a r c t a n x x \lim_{x \to \infty} \frac{arctanx}{x} limx→∞xarctanx = 0
6.重要极限
- lim x → 0 s i n x x \lim_{x \to 0} \frac{sinx}{x} limx→0xsinx = 1
- lim x → ∞ ( 1 + 1 x ) x \lim_{x \to \infty}(1 + \frac{1}{x})^x limx→∞(1+x1)x = e
- lim x → 0 ( 1 + x ) 1 x \lim_{x \to 0}(1 + x)^{\frac{1}{x}} limx→0(1+x)x1 = e
其中第二和第三点可以归纳为:
lim x → 0 ( 1 + 1 f ( x ) ) 1 f ( x ) \lim_{x \to 0}({1 + \frac{1}{f(x)}})^\frac{1}{f(x)} limx→0(1+f(x)1)f(x)1 = e
7.夹逼定理的应用
例6
lim x → ∞ n ( 1 n 2 + π + 1 n 2 + 2 π + . . . + 1 n 2 + n π ) \lim_{x \to \infty}n(\frac{1}{n^2+\pi}+\frac{1}{n^2+2\pi}+...+\frac{1}{n^2+n\pi}) limx→∞n(n2+π1+n2+2π1+...+n2+nπ1)
解:
因为: 1 n 2 + π \frac{1}{n^2+\pi} n2+π1 > 1 n 2 + i π \frac{1}{n^2+i\pi} n2+iπ1 > 1 n 2 + n π \frac{1}{n^2+n\pi} n2+nπ1
所以:
n n 2 + π \frac{n}{n^2+\pi} n2+πn> 1 n 2 + π + 1 n 2 + 2 π + . . . + 1 n 2 + n π \frac{1}{n^2+\pi}+\frac{1}{n^2+2\pi}+...+\frac{1}{n^2+n\pi} n2+π1+n2+2π1+...+n2+nπ1> n n 2 + n π \frac{n}{n^2+n\pi} n2+nπn
n 2 n 2 + π \frac{n^2}{n^2+\pi} n2+πn2>n( 1 n 2 + π + 1 n 2 + 2 π + . . . + 1 n 2 + n π \frac{1}{n^2+\pi}+\frac{1}{n^2+2\pi}+...+\frac{1}{n^2+n\pi} n2+π1+n2+2π1+...+n2+nπ1)> n 2 n 2 + n π \frac{n^2}{n^2+n\pi} n2+nπn2
而: lim x → ∞ n 2 n 2 + π \lim_{x \to \infty}\frac{n^2}{n^2+\pi} limx→∞n2+πn2 = lim x → ∞ n 2 n 2 + n π \lim_{x \to \infty}\frac{n^2}{n^2+n\pi} limx→∞n2+nπn2 = 1
则:原式
= lim x → ∞ n ( 1 n 2 + π + 1 n 2 + 2 π + . . . + 1 n 2 + n π ) \lim_{x \to \infty}n(\frac{1}{n^2+\pi}+\frac{1}{n^2+2\pi}+...+\frac{1}{n^2+n\pi}) limx→∞n(n2+π1+n2+2π1+...+n2+nπ1)
= 1
淦 终于到最后一点了 LaTeX数学公式给我写懵了
8.等价无穷小的代换
常见的等价无穷小有:
sin x \sin x sinx ∼ \sim ∼ x
tan x \tan x tanx ∼ \sim ∼ x
arctan x \arctan x arctanx ∼ \sim ∼ x
arcsin x \arcsin x arcsinx ∼ \sim ∼ x
注意:等价无穷小的替换只能在乘积里面出现
( a − b ) c d \frac{(a-b)c}{d} d(a−b)c
其中只有c和d可以做无穷小的等价替换
例7
lim x → 0 tan x − sin x sin 3 x \lim_{x \to 0}\frac{\tan x - \sin x}{\sin^3 x} limx→0sin3xtanx−sinx
此处不能直接对tanx和sinx做等价无穷小的代换
解:
原式
= lim x → 0 tan x ( 1 − cos x ) x 3 \lim_{x \to 0}\frac{\tan x(1 - \cos x) }{x^3} limx→0x3tanx(1−cosx)
= lim x → 0 ( 1 − cos x ) x 2 \lim_{x \to 0}\frac{ (1 - \cos x) }{x^2} limx→0x2(1−cosx)
= lim x → 0 1 2 x 2 x 2 \lim_{x \to 0}\frac{ \frac{1}{2} x^2 }{x^2} limx→0x221x2
= 1 2 \frac{1}{2} 21
例8
lim x → 0 sin x − tan x ( ( 3 1 + x 2 ) − 1 ) ( 1 + sin x − 1 ) \lim_{x \to 0}\frac{\sin x - \tan x}{(\sqrt[3](1+x^2) - 1)(\sqrt1+\sin x -1)} limx→0(3(1+x2)−1)(1+sinx−1)sinx−tanx
解:
原式
= lim x → 0 tan x ( cos x − 1 ) 1 3 x 2 ∗ 1 2 sin x \lim_{x \to 0}\frac{\tan x( \cos x - 1) }{\frac{1}{3}x^2*\frac{1}{2}\sin x} limx→031x2∗21sinxtanx(cosx−1)
= lim x → 0 x ( − 1 2 x 2 ) 1 6 x 3 \lim_{x \to 0}\frac{x(-\frac{1}{2} x^2)}{\frac{1}{6} x^3} limx→061x3x(−21x2)
= -3
DAY 1 DONE