目标检测中的性能提升方法综述
文章目录
- 一,多尺度检测
-
- 什么是多尺度检测?
- 降低下采样率与空洞卷积
- 多尺度训练
- 优化Anchor尺寸训练
- 深层与浅层特征融合
- SNIP,尺度归一化
- TridentNet,三叉戟网络
- 总结
- 二,目标检测中的样本不均衡问题
-
- 什么是目标检测样本不均衡问题
- 1,OHEM,在线难例挖掘
- 2,S-OHEM,基于LOSS分布采样的在线困难样本挖掘
- 3,Focal Loss :专注难样本
- 4, Generalized Focal Loss
- 5,GHM,损失函数梯度均衡化机制
- 总结
- 三,目标检测优化使用的Trick
-
- 1,数据预处理技巧
- 2,模型训练参数调整
- 四,小目标检测常用解决方案
-
-
- 传统的图像金字塔和多尺度滑动窗口检测
- 简单粗暴可靠的数据增强
- 特征融合的FPN
- 合适的训练方法SNIP,SNIPER,SAN
- 更稠密的Anchor采样和匹配策略S3FD,FaceBoxes
- 先生成放大特征再检测的GAN
- 利用Context信息的Relation Network和PyramidBox
-
- 五,目标检测多模型集成方法
-
- 不同的集成方式
- 检测框加权融合
- 六.对Anchor的优化
-
- 1.Anchor refinement module (ARM)
本文从 降低下采样率与 空洞卷积、 多尺度训练、 优化Anchor尺寸设计、 深层和浅层特征融合等多个方面入手,对目标检测中的多尺度检测方法进行了全面概述,并介绍了多尺度检测相关方法。
受感受野大小的影响,存在如下结论**:对于大物体而言,其语义信息将出现在较深的特征图中(每个特征点对应的感受野较大);而对于小物体,其语义信息出现在较浅的特征图中(每个特征点对应的感受野较小),随着网络的加深,其细节信息可能会完全消失。**
一,多尺度检测
什么是多尺度检测?
多尺度是目标检测和图像分类的主要区别。分类问题主要针对同一中尺度,而目标检测,模型需要对不同尺度的物体检测出来,要求模型具有鲁棒性。
在多尺度的物体中,大尺度的物体由于面积大、特征丰富,通常来讲较为容易检测。难度较大的主要是小尺度的物体,而这部分小物体在实际工程中却占据了较大的比例。通常认为绝对尺寸小于32×32的物体,可以视为小物体或者物体宽高是原图宽高的1/10以下,可以视为小物体。
小物体的特征相对较少,检测较为困难,当前的检测算法对于小物体的检测并不友好,体现在以下四个方面:
1,过大的下采样率:假设当前的小物体的尺寸是15*15,一般的物体检测中卷积下采样率为16,这样在特征图中,过大的下采样率使得小物体两一个像素点都占据不到。
2,过大的感受野:在卷积网络中,特征图上特征点的感受野比下采样率大很多,导致在特征图上的一个点中,小物体占据的特征更少,会包含大量周围区域的特征,从而影响其检测结果。
3,语义与空间的矛盾
当前检测算法,如Faster RCNN,其Backbone大都是自上到下的方式,深层与浅层特征图在语义性与空间性上没有做到更好的均衡。
4,SSD一阶算法缺少特征融合
SSD虽然使用了多层特征图,但浅层的特征图语义信息不足,没有进行特征的融合,致使小物体检测的结果较差。
多尺度的检测能力实际上体现了尺度的不变性,当前的卷积网络能够检测多种尺度的物体,很大程度上是由于其本身具有超强的拟合能力。
降低下采样率与空洞卷积可以显著提升小物体的检测性能;设计更好的Anchor可以有效提升Proposal的质量;多尺度的训练可以近似构建出图像金字塔,增加样本的多样性;特征融合可以构建出特征金字塔,将浅层与深层特征的优势互补。
下面介绍较为通用的提高多尺度目标检测的方法:
降低下采样率与空洞卷积
对于小物体检测而言,降低网络的下采样率通常的做法是直接去除掉Pooling层。
例如,将原始的VGGNet-16作为物体检测的Backbone时,通常是将第5个Pooling层之前的特征图作为输出的特征图,一共拥有4个Pooling层,这时下采样率为16。为了降低下采样率,我们可以将第4个Pooling层去掉,使得下采样率变为8,减少了小物体在特征图上的信息损失。
但是,如果仅仅去除掉Pooling层,则会减小后续层的感受野。如果使用预训练模型进行微调(Fine-tune),则仅去除掉Pooling层会使得后续层感受野与预训练模型对应层的感受野不同,从而导致不能很好地收敛。
因此,需要在去除Pooling的前提下增加后续层的感受野,使用空洞卷积可以在保证不改变网络分辨率的前提下增加网络的感受野。
需要注意的是,采用空洞卷积也不能保证修改后与修改前的感受野完全相同,但能够最大限度地使感受野在可接受的误差内。
多尺度训练
多尺度类似于数字图像处理中的图像金字塔,即将输入图片缩放到多个尺度下,每一个尺度单独地计算特征图,并进行后续的检测。这种方式虽然一定程度上可以提升检测精度,但由于多个尺度完全并行,耗时巨大。
多尺度训练(Multi Scale Training, MST)通常是指设置几种不同的图片输入尺度,**训练时从多个尺度中随机选取一种尺度,将输入图片缩放到该尺度并送入网络中,**是一种简单又有效的提升多尺度物体检测的方法。
虽然一次迭代时都是单一尺度的,但每次都各不相同,增加了网络的鲁棒性,又不至于增加过多的计算量。而在测试时,为了得到更为精准的检测结果,也可以将测试图片的尺度放大,例如放大4倍,这样可以避免过多的小物体。
多尺度训练是一种十分有效的trick方法,放大了小物体的尺度,同时增加了多尺度物体的多样性,在多个检测算法中都可以直接嵌入,在不要求速度的场合或者各大物体检测竞赛中尤为常见。
优化Anchor尺寸训练
现今较为成熟的检测算法大都采用Anchor作为先验框,如Faster RCNN和SSD,YOLO等。模型在Anchor的基础上只需要去预测其与真实物体边框的偏移即可,可以说是物体检测算法发展中的一个相当经典的设计。
Anchor通常是多个不同大小与宽高的边框,这个大小与宽高是一组超参数,需要我们手动配置。在不同的数据集与任务中,由于物体的尺度、大小会有差距,例如行人检测的数据集中,行人标签宽高比通常为0.41,与通用物体的标签会有所区别,这时就需要相应地调整Anchor的大小与宽高。
如果Anchor设计的不合理,与数据集中的物体分布存在差距,则会给模型收敛带来较大的困难,影响模型的精度,甚至不会收敛。
另外,Anchor的设计对于小物体的检测也尤为重要,如果Anchor过大,即使小物体全部在Anchor内,也会因为其自身面积小导致IoU低,从而造成漏检。
1. 统计实验,手工设计
在Faster RCNN的RPN阶段,所有Anchor会与真实标签进行匹配,根据匹配的IoU值得到正样本与负样本,正样本的IoU阈值为0.7。在这个过程中,Anchor与真实标签越接近,正样本的IoU会更高,RPN阶段对于真实标签的召回率会越高,正样本也会更丰富,模型效果会更好。
因此,可以仅仅利用训练集的标签与设计的Anchor进行匹配试验,试验的指标是所有训练标签的召回率,以及正样本的平均IoU值。当然,也可以增加每个标签的正样本数、标签的最大IoU等作为辅助指标。
为了方便地匹配,在此不考虑Anchor与标签的位置偏移,而是把两者的中心点放在一起,仅仅利用其宽高信息进行匹配。这种统计实验实际是通过手工设计的方式,寻找与标签宽高分布最为一致的一组Anchor。
2. 边框聚类
相比起手工寻找标签的宽高分布,也可以利用聚类的思想,在训练集的标签上直接聚类出一组合适的Anchor。由于一组Anchor会出现在特征图的每一个位置上,因此没有位置区别,可以只关注标签里的物体宽高,而没必要关心物体出现的位置。
边框聚类时通常使用K-Means算法,这也是YOLO采用的Anchor聚类方法。K-Means算法输入超参数K,即最终想要获得的边框数量,首先随机选取K个中心点,然后遍历所有的数据,并将所有的边框划分到最近的中心点中。在每个边框都落到不同的聚类后,计算每一个聚类的平均值,并将此平均值作为新的中心点。重复上述过程,直到算法收敛。
在聚类过程中,**Anchor的数量K是一个较为重要的超参,数量越多,精度越高,**但与此同时会带来计算量的增加。对于使用Anchor的物体检测算法而言,设计一组好的Anchor是基础,这对于多尺度、拥挤等问题都有较大的帮助。
深层与浅层特征融合
传统的卷积网络通常是自上而下的模式,随着网络层数的增加,感受野会增大,语义信息也更为丰富。这种自上而下的结构本身对于多尺度的物体检测就存在弊端,尤其是小物体,其特征可能会随着深度的增加而渐渐丢失,从而导致检测性能的降低。
可以将深层的语义信息添加到浅层的特征图中,融合两者的特征,优势互补,从而提升对于小物体的检测性能。
特征融合有多种方式,**增大特征图尺寸可以使用上采样、反卷积****等,融合方法有逐元素相加、相乘和通道拼接等,具体哪种效果更好,还要看实际的检测任务及使用的检测算法。特征融合的普遍缺点是通常会带来一定计算量的增加。
也可以使用多尺度预测,YOLOV3采用的这种方法
特征融合方法示例:
1.FPN(Feature Pyramid Network)
将深层信息上采样,与浅层信息逐元素地相加,从而构建了尺寸不同的特征金字塔结构,性能优越,现已成为目标检测算法的一个标准组件。FPN的结构如下所示。

上图网络代码实现:
import torch.nn as nn
import torch.nn.functional as F
import math
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, in_planes, planes, stride=1, downsample=None):
super(Bottleneck, self).__init__()
self.bottleneck = nn.Sequential(
nn.Conv2d(in_planes, planes, 1, bias=False),
nn.BatchNorm2d(planes),
nn.ReLU(inplace=True),
nn.Conv2d(planes, planes, 3, stride, 1, bias=False),
nn.BatchNorm2d(planes),
nn.ReLU(inplace=True),
nn.Conv2d(planes, self.expansion * planes, 1, bias=False),
nn.BatchNorm2d(self.expansion * planes),
)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
def forward(self, x):
identity = x
out = self.bottleneck(x)
if self.downsample is not None:
identity = self.downsample(x)
out += identity
out = self.relu(out)
return out
class FPN(nn.Module):
def __init__(self, layers):
super(FPN, self).__init__()
self.inplanes = 64
self.conv1 = nn.Conv2d(3, 64, 7, 2, 3, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(3, 2, 1)
self.layer1 = self._make_layer(64, layers[0])#输出尺寸,网络层位置
self.layer2 = self._make_layer(128, layers[1], 2)
self.layer3 = self._make_layer(256, layers[2], 2)
self.layer4 = self._make_layer(512, layers[3], 2)
self.toplayer = nn.Conv2d(2048, 256, 1, 1, 0)
self.smooth1 = nn.Conv2d(256, 256, 3, 1, 1)#输入,输出,尺寸,步长,padding
self.smooth2 = nn.Conv2d(256, 256, 3, 1, 1)
self.smooth3 = nn.Conv2d(256, 256, 3, 1, 1)
self.latlayer1 = nn.Conv2d(1024, 256, 1, 1, 0)
self.latlayer2 = nn.Conv2d( 512, 256, 1, 1, 0)
self.latlayer3 = nn.Conv2d( 256, 256, 1, 1, 0)
def _make_layer(self, planes, blocks, stride=1):
downsample = None
if stride != 1 or self.inplanes != Bottleneck.expansion * planes:
downsample = nn.Sequential(
nn.Conv2d(self.inplanes, Bottleneck.expansion * planes, 1, stride, bias=False),
nn.BatchNorm2d(Bottleneck.expansion * planes)
)
layers = []
layers.append(Bottleneck(self.inplanes, planes, stride, downsample))
self.inplanes = planes * Bottleneck.expansion
for i in range(1, blocks):
layers.append(Bottleneck(self.inplanes, planes))
return nn.Sequential(*layers)
def _upsample_add(self, x, y):
_,_,H,W = y.shape
return F.upsample(x, size=(H,W), mode='bilinear') + y#线性插值resize
def forward(self, x):
c1 = self.maxpool(self.relu(self.bn1(self.conv1(x))))#普通的卷积
c2 = self.layer1(c1)#resnet网络块
c3 = self.layer2(c2)
c4 = self.layer3(c3)
c5 = self.layer4(c4)
p5 = self.toplayer(c5)
p4 = self._upsample_add(p5, self.latlayer1(c4))#p5上采样后与c4 1*1卷积后加
p3 = self._upsample_add(p4, self.latlayer2(c3))
p2 = self._upsample_add(p3, self.latlayer3(c2))
p4 = self.smooth1(p4)#3*3卷积
p3 = self.smooth2(p3)
p2 = self.smooth3(p2)
return p2, p3, p4, p5
2,DetNet
专为目标检测而生的Backbone,利用空洞卷积与残差结构,使得多个融合后的特征图尺寸相同,从而也避免了上采样操作。
3,HyperNet
Faster RCNN系列中,HyperNet将第1、3、5个卷积组后得到的特征图进行融合,浅层的特征进行池化、深层的特征进行反卷积,最终采用通道拼接的方式进行融合,优势互补。
4,SSD系列中,DSSD在SSD的基础上,对深层特征图进行反卷积,与浅层的特征相乘,得到了更优的多层特征图,这对于小物体的检测十分有利。
5.RefineDet将SSD的多层特征图结构作为了Faster RCNN的RPN网络,结合了两者的优点。特征图处理上与FPN类似,利用反卷积与逐元素相加,将深层特征图与浅层的特征图进行结合,实现了一个十分精巧的检测网络。
SNIP,尺度归一化
论文地址:https://arxiv.org/abs/1711.08189
代码实现:https://github.com/mahyarnajibi/SNIPER
检测任务算法通常会采用微调的方法,即先在图像分类数据集比如ImageNet数据集上训练分类任务,然后再迁移到物体检测的数据集上,如COCO来训练检测任务。我们可以将ImageNet的分类任务看做224×224的尺度,而COCO中的物体尺度大部分在几十像素的范围内,并且包含大量小物体,物体尺度差距更大,因此两者的样本差距太大,会导致映射迁移(Domain Shift)的误差。
SNIP是MST(多尺度训练)的改进,MST的思想是使用随机采样的多分辨率图像使得检测器具有尺度不变性。然而作者通过实验发现,在MST中,对于极大目标和过小目标的检测效果并不好,但是MST也有一些优点,比如对一张图片会有几种不同分辨率,每个目标在训练时都会有几个不同的尺寸,那么总有一个尺寸在指定的尺寸范围内。
SNIP的做法是只对size在指定范围内的目标回传损失,即训练过程实际只是针对某些特定的目标进行,这样就能减少domain-shift带来的影响。
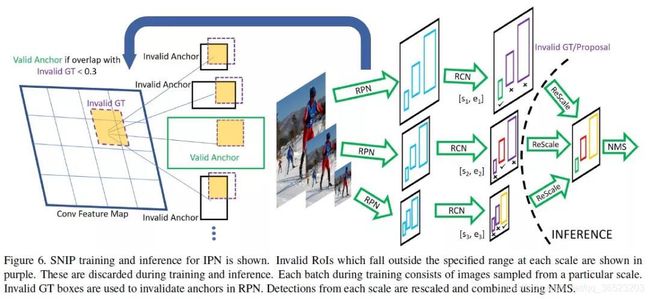
算法流程:
-
3个尺度分别拥有各自的RPN模块,并且各自预测指定范围内的物体。
-
对于大尺度的特征图,其RPN只负责预测被放大的小物体,对于小尺度的特征图,其RPN只负责预测被缩小的大物体,这样真实的物体尺度分布在较小的区间内,避免了极大或者极小的物体。
-
在RPN阶段,如果真实物体不在该RPN预测范围内,会被判定为无效,并且与该无效物体的IoU大于0.3的Anchor也被判定为无效的Anchor。
-
在训练时,只对有效的Proposal进行反向传播。在测试阶段,对有效的预测Boxes先缩放到原图尺度,利用Soft NMS将不同分辨率的预测结果合并。
-
实现时SNIP采用了可变形卷积的卷积方式,并且为了降低对于GPU的占用,将原图随机裁剪为1000×1000大小的图像。
总体来说,SNIP让模型更专注于物体本身的检测,剥离了多尺度的学习难题。在网络搭建时,SNIP也使用了类似于MST的多尺度训练方法,构建了3个尺度的图像金字塔,但在训练时,只对指定范围内的Proposal进行反向传播,而忽略掉过大或者过小的Proposal。
SNIP方法虽然实现简单,但其背后却蕴藏深意,更深入地分析了当前检测算法在多尺度检测上的问题所在,在训练时只选择在一定尺度范围内的物体进行学习,在COCO数据集上有3%的检测精度提升,可谓是大道至简。
TridentNet,三叉戟网络
论文:https://arxiv.org/abs/1901.01892
代码:https://github.com/TuSimple/simpledet/tree/master/models/tridentnet
传统的解决多尺度检测的算法,大豆依赖于图像金字塔与特征金字塔。与上述算法不同,图森组对感受野这一因素进行了深入的分析,并利用了空洞卷积这一利器,构建了简单的三分支网络TridentNet,对于多尺度物体的检测有了明显的精度提升。
TridentNet网络的作者将3种不同的感受野网络并行化,提出了如下图所示的检测框架。采用ResNet作为基础Backbone,前三个stage沿用原始的结构,在第四个stage,使用了三个感受野不同的并行网络。
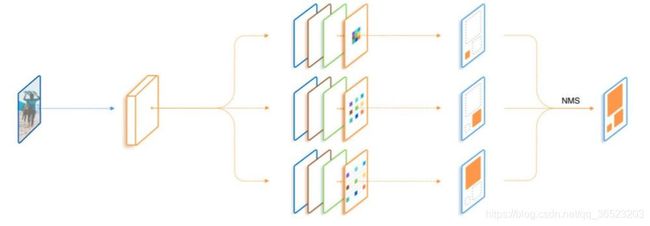
算法流程:
- 3个不同的分支使用空洞数不同的空洞卷积,感受野由小到大。可以更好地覆盖多尺度的物体分布。
- 由于3个分支要检测的内容是相同的、要学习的特征也是相同的,只不过是形成了不同的感受野来检测不同尺度的物体,因此,3个分支共享权重,这样既充分利用了样本信息,学习到更本质的目标检测信息,也减少了参数量与过拟合的风险。
- 借鉴了SNIP的思想,在每一个分支内只训练一定范围内的样本,避免了过大与过小的样本对于网络参数的影响。
在训练时,TridentNet网络的三个分支会接入三个不同的head网络进行后续损失计算。在测试时,由于没有先验的标签来选择不同的分支,因此只保留了一个分支进行前向计算,这种前向方法只有少量的精度损失。
总结
二,目标检测中的样本不均衡问题
什么是目标检测样本不均衡问题
当前主流的目标检测算法中,Faster CNN和SSD将目标检测当做分类问题来考虑,即先使用先验框或者RPN等生成感兴趣的区域,再对该区域进行分类与回归位置。这种基于分类思想的目标(YOLO是基于回归思想)检测算法存在样本不平衡的问题,因而会降低模型的训练效率与检测精度。
样本不均衡问题:
指在训练的时候各个类别的样本数量不均衡,由于检测算法各不相同,以及数据集之间的差异,可能会存在正负样本、难易样本、类别间样本这3种不均衡问题。一般在目标检测任务框架中,保持正负样本的比例为1:3(经验值)。
样本不平衡实际上是一种非常常见的现象。比如:在欺诈交易检测,欺诈交易的订单应该是占总交易数量极少部分;工厂中产品质量检测问题,合格产品的数量应该是远大于不合格产品的;信用卡的征信问题中往往就是正样本居多。困难样本一般样本在总数比例很小。
目标检测任务中,样本包含的类别:
-
正样本: 标签区域内的图像区域,即目标图像块。
-
负样本:标签区域外的图像区域,即背景图像块。
-
易分正样本:容易被正确分类的正样本,在实际的训练中,该类占总样本的比重非常高,单个样本的损失函数较小,但是累积的损失函数会主导损失函数。
-
易分负样本:容易正确分类的负样本,在实际训练过程中,该类占的比重非常高,单个样本的损失函数较小,但是累计的损失函数会主导损失函数
-
难分正样本:错分成负样本的正样本,这部分样本在训练过程中单个样本的损失函数较高,但是该类占总体样本的比例较小。
-
难分负样本:错分成正样本的负样本,这部分样本在训练过程中单个样本的损失函数教高,但是该类占总体样本的比例教小。
样本不均衡存在以下情况:
1. 正负样本不均衡
以Faster RCNN为例,在RPN部分会生成20000个左右的Anchor,由于一张图中通常有10个左右的物体,导致可能只有100个左右的Anchor会是正样本,正负样本比例约为1∶200,存在严重的不均衡。
负样本对应着图像的背景,如果有大量的负样本参与训练,则会淹没正样本的损失,从而降低网络收敛的效率与检测精度
2.难易样本不平衡
一般难样本较少,简单样本很多。难样本损失较大,可以利用这部分训练提升目标检测的真确率,但是简单样本多,损失小但是优于数量众多,最后损失也会比难样本大,这种难易样本的不均衡也会影响模型的收敛速度与精度。
**值得注意的是:**负样本中大量的简单样本,导致难易样本与正负样本的两个不均衡问题有一定的重叠,解决方法往往能同时对这两个问题起作用。
3.类别间样本不均衡
在有些目标检测的数据集中,还会存在类别间的不均衡问题。举个例子,数据集中有100万个车辆、1000个行人的实例标签,样本比例为1000∶1,属于典型的类别不均衡。
这种情况下,如果不做任何处理,使用该数据集进行训练,由于行人这一类别可参考标签太少,会使得模型主要关注车这一类别的检测,网络中的参数主要根据车辆的损失进行优化,导致行人的检测精度大大下降。
目前,解决样本不均衡问题的主要包括2种思路:数据角度和算法角度。数据角度有:扩大数据集,数据类别均衡采样。在算法层面,目标检测方法使用的有:
- Faster RCNN、SSD等算法在正负样本的筛选时,根据样本与真实物体的IoU大小,设置了3∶1的正负样本比例,这一点缓解了正负样本的不均衡,同时也对难易样本不均衡起到了作用。
- Faster RCNN在RPN模块中,通过前景得分排序筛选出了2000个左右的候选框,这也会将大量的负样本与简单样本过滤掉,缓解了前两个不均衡问题。
- reweight:对于难易样本与类别间的不均衡,可以增大难样本与少类别的损失权重,从而增大模型对这些样本的惩罚,缓解不均衡问题。
- **resample:**从数据侧入手,可以在当前数据集上使用随机生成和添加扰动的方法,也可以利用网络爬虫数据等增加数据集的丰富性,从而缓解难易样本和类别间样本等不均衡问题,可以参考SSD的数据增强方法。
最近比较新的研究方法包括:
1,OHEM,在线难例挖掘
2016年CVPR论文
论文地址:https://arxiv.org/pdf/1604.03540.pdf
算法主要针对训练过程中的困难样本自动选择,核心思想是根据输入样本的损失进行筛选,筛选出看困难样本(对分类和检测影响较大的样本),然后将筛选出得到的这些困难样本应用在随机梯度下降中训练。
传统的Fast RCNN系列算法RPN在正负样本选择的时候采用当前RoI与真实物体的IoU阈值比较的方法,这样容易忽略一些较为重要的难负样本,并且固定了正、负样本的比例与最大数量,显然不是最优选择。以此为出发点,OHEM将交替训练与SGD优化方法进行了结合,在每张图片的RoI中选择了较难的样本,实现了在线的难样本挖掘。
实现在想困难样本挖掘网络如图所示:
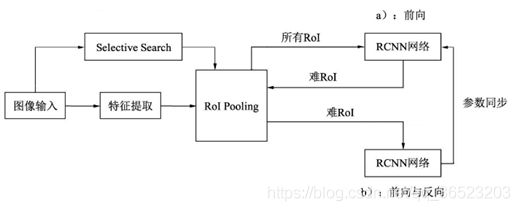
算法流程:
- 按照原始Fast RCNN算法,经过卷积网络与RoI pooling得到每一张图像的RoI。
- 上半部的a网络对所有的RoI进行前向计算,得到每一个RoI的损失。
- 对RoI的损失进行排序,进行一步NMS操作,以去除掉重叠严重的RoI,并在筛选后的RoI中选择出固定数量损失较大的部分,作为难样本。
- 将筛选出的难样本输入到可读写的b网络中,进行前向计算,得到损失。
- 利用b网络得到的反向传播更新网络(达到了使用困难样本训练网络的目的),并将更新后的参数与上半部的a网络同步,完成一次迭代。
可以将OHEM简单实现:在原有的Fast-RCNN里的loss layer里面对所有的props计算其loss,根据loss对其进行排序,选出K个hard examples,反向传播时,只对这K个props的梯度/残差回传,而其他的props的梯度/残差设为0。
但是,由于其特殊的损失计算方式,把简单的样本都舍弃了,导致模型无法提升对于简单样本的检测精度,这也是OHEM方法的一个弊端。
-
优点:1,对于数据的类别不平衡问题不需要采用设置正负样本比例的方式来解决,这种在线选择方式针对性更强;2,随着数据集的增大,算法的提升更加明显
-
缺点:只保留loss较高的样本,完全忽略简单的样本,这本质上是改变了训练时的输入分布(仅包含困难样本),这会导致模型在学习的时候失去对简单样本的判别能力。
2,S-OHEM,基于LOSS分布采样的在线困难样本挖掘
在目标检测的任务中,一般包含两种损失:1,分类损失 L c l s L_{cls} Lcls 2,定位损失 L l o c L_{loc} Lloc,OHEM的方法忽略训练过程中不同损失类型的影响,例如在训练后期,定位损失更为重要,因此OHEM缺乏对定位精度的足够关注。
S-OHEM算法采用了分层抽样的方法,根据LOSS分布抽样训练样本。预设loss的四个阶段。
1, h i g h L c l s , h i g h L l o c highL_{cls},highL_{loc} highLcls,highLloc
2, h i g h L c l s , l o w L l o c highL_{cls},lowL_{loc} highLcls,lowLloc
3, l o w L c l s , h i g h L l o c lowL_{cls},highL_{loc} lowLcls,highLloc
4, l o w L c l s , l o w L l o c lowL_{cls},lowL_{loc} lowLcls,lowLloc
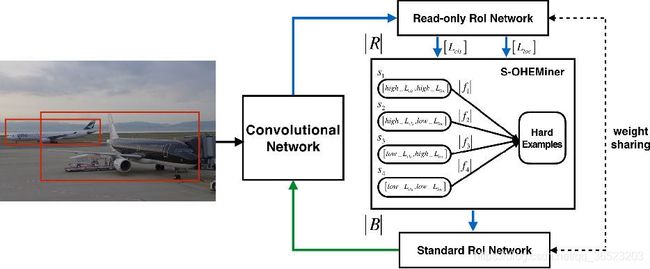
S-OHEM是OHEM的改进,训练网络如上图所示,给定一个batch,先生成输入batch中所有图像的候选RoI,再将这些RoI送入到Read only RoI网络得到RoIs的损失,然后将每个RoI计算损失并划分到上面四个分段中,然后针对每个分段,通过排序筛选困难样本(损失大的样本).再将经过筛选的RoIs送入反向传播,用于更新网络参数。网络中使用损失形式为 L s e l e c t = α ∗ L c l s + β ∗ L l o c L_{select}=\alpha *L_{cls}+\beta*L_{loc} Lselect=α∗Lcls+β∗Lloc,随着训练的进行,在训练初期阶段,分类损失占主导作用;在训练后期阶段,边框回归损失函数占主导作用。
如上图所示,网络主要包括两个部分:ConvNet和RoiNet。RoINet又可看成两部分:Read-only RoI Network和Standard RoI Network。
图中R表示向前传播的RoI的数量,B表示被馈送到反向传播的子采样的RoI的数量。S-OHEMiner根据当前训练阶段的采样分布对region proposals进行抽样(困难样本选择)。Read-only RoI Network只有forward操作,Standard RoI Network包括forward和backward操作,以hard example作为输入,计算损失并回传梯度。
RoINet的两部分共享权重,可实现高效地分配内存。在图中,蓝色箭头表示向前传播的过程,绿色箭头表示反向传播过程。
相比原生OHEM,S-OHEM考虑了基于不同损失函数的分布来抽样选择困难样本,避免了仅使用高损失的样本来更新模型参数。
缺点:
因为不同阶段,分类损失和定位损失的贡献不同,所以选择损失中的两个参数 α 和 β \alpha和\beta α和β 需要根据不同训练阶段进行改变,当应用与不同数据集时,参数的选取也是不一样的。即引入了额外的超参数。
3,Focal Loss :专注难样本
论文:https://arxiv.org/abs/1708.02002
代码:基于pytorch的实现
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class FocalLoss(nn.Module):
r"""
This criterion is a implemenation of Focal Loss, which is proposed in
Focal Loss for Dense Object Detection.
Loss(x, class) = - \alpha (1-softmax(x)[class])^gamma \log(softmax(x)[class])
The losses are averaged across observations for each minibatch.
Args:
alpha(1D Tensor, Variable) : the scalar factor for this criterion
gamma(float, double) : gamma > 0; reduces the relative loss for well-classified examples (p > .5),
putting more focus on hard, misclassified examples
size_average(bool): By default, the losses are averaged over observations for each minibatch.
However, if the field size_average is set to False, the losses are
instead summed for each minibatch.
"""
def __init__(self, class_num, alpha=None, gamma=2, size_average=True):
super(FocalLoss, self).__init__()
if alpha is None:
self.alpha = Variable(torch.ones(class_num, 1))
else:
if isinstance(alpha, Variable):
self.alpha = alpha
else:
self.alpha = Variable(alpha)
self.gamma = gamma
self.class_num = class_num
self.size_average = size_average
def forward(self, inputs, targets):
N = inputs.size(0)
C = inputs.size(1)
P = F.softmax(inputs)
class_mask = inputs.data.new(N, C).fill_(0)
class_mask = Variable(class_mask)
ids = targets.view(-1, 1)
class_mask.scatter_(1, ids.data, 1.)
#print(class_mask)
if inputs.is_cuda and not self.alpha.is_cuda:
self.alpha = self.alpha.cuda()
alpha = self.alpha[ids.data.view(-1)]
probs = (P*class_mask).sum(1).view(-1,1)
log_p = probs.log()
#print('probs size= {}'.format(probs.size()))
#print(probs)
batch_loss = -alpha*(torch.pow((1-probs), self.gamma))*log_p
#print('-----bacth_loss------')
#print(batch_loss)
if self.size_average:
loss = batch_loss.mean()
else:
loss = batch_loss.sum()
return loss
当前一阶的物体检测算法,如SSD和YOLO等虽然实现了实时的速度,但精度始终无法与两阶的Faster RCNN相比。是什么阻碍了一阶算法的高精度呢?何凯明等人将其归咎于正、负样本的不均衡,并基于此提出了新的损失函数Focal Loss及网络结构RetinaNet,在与同期一阶网络速度相同的前提下,其检测精度比同期最优的二阶网络还要高。
对于SSD等一阶网络,由于其需要直接从所有的预选框中进行筛选,即使使用了固定正、负样本比例的方法,仍然效率低下,简单的负样本仍然占据主要地位,导致其精度不如两阶网络。为了解决一阶网络中样本的不均衡问题,何凯明等人首先改善了分类过程中的交叉熵函数,提出了可以动态调整权重的Focal Loss。
1.标准交叉熵损失函数
C E ( p , y ) = − l o g ( p ) i f ( y = 1 ) e l s e − l o g ( 1 − p ) CE(p,y)=-log(p) if (y=1) else -log(1-p) CE(p,y)=−log(p)if(y=1)else−log(1−p)
p越接近y标签,损失越小
公式中,p代表样本在该类别的预测概率,y代表样本标签。可以看出,当标签为1时,p越接近1,则损失越小;标签为0时p越接近0,则损失越小,符合优化的方向。
可以看出,标准的交叉熵中所有样本的权重都是相同的,因此如果正、负样本不均衡,大量简单的负样本会占据主导地位,少量的难样本与正样本会起不到作用,导致精度变差。
2.平衡交叉熵损失函数
为了改善样本的不平衡问题,平衡交叉熵在标准的基础上增加了一个系数 α t \alpha_t αt来平衡正、负样本的权重, α t \alpha_t αt由超参 α \alpha α按照下式计算得来, α \alpha α取值在[0,1]区间内。
α t = α i f ( y = 1 ) e l s e 1 − α \alpha_t=\alpha if (y=1) else 1-\alpha αt=αif(y=1)else1−α
有了 α \alpha α,平衡交叉熵损失公式如下所示。 C E ( p t ) = − α t l o g ( p t ) CE(p_t)=-\alpha_tlog(p_t) CE(pt)=−αtlog(pt)
y=1是正样本,平衡交叉熵损失改善了正负样本的不均衡。
3.专注难样本Focal loss
Focal Loss为了同时调节正、负样本与难易样本,提出了如下所示的损失函数。在平衡交叉熵损失函数上的改进:
F L ( p t ) = − α t ( 1 − p t ) y l o g ( p t ) FL(p_t)=-\alpha_t(1-p_t)^ylog(p_t) FL(pt)=−αt(1−pt)ylog(pt)
其中 α t \alpha_t αt用于控制正负样本的权重,取比较小的值降低负样本(样本多的类)的权重; ( 1 − p t ) y (1-p_t)^y (1−pt)y用于控制难易样本的权重,目的是通过减少易分样本的权重,从而使得模型在训练时候更关注难分样本的学习。文章中批量实验验证,当 α t = 0.25 , y = 2 \alpha_t=0.25,y=2 αt=0.25,y=2时效果最好。
可以看出,对于 Focal Loss损失函数,有如下3个属性:
- 与平衡交叉熵类似, α t \alpha_t αt改善正负样本的不均衡,可以提升一些精度
- ( 1 − p t ) y (1-p_t)^y (1−pt)y是为了调节难易样本的权重。当一个边框被误分类时, p t p_t pt较小,则 ( 1 − p t ) y (1-p_t)^y (1−pt)y接近1,损失几乎不受影响,当pt接近于1时,表明其分类预测较好,是简单样本, ( 1 − p t ) y (1-p_t)^y (1−pt)y接近于0,因此其损失被调低了。所以,更加关注困难样本
- y y y是调制因子,越大,简单样本损失的贡献越小
为了验证Focal Loss的效果,何凯明等人还提出了一个一阶物体检测结构RetinaNet,其结构如下图所示。
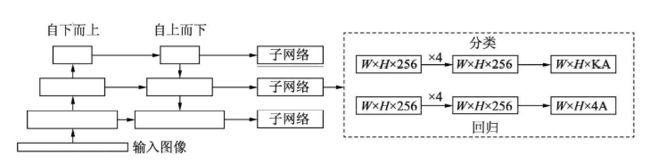
关于RetinaNet,有5个细节:
1,在Backbone部分,RetinaNet利用ResNet与FPN构建了一个多尺度特征的特征金字塔,自下而上后自上而下。
2,RetinaNet使用类似于Anchor的预选框,在每一个金字塔层,使用了9个大小不同的预选框。
3,分类子网络:分类子网络为每一个预选框预测其类别,因此其输出特征大小为KA×W×H, A默认为9, K代表类别数。中间使用全卷积网络与ReLU激活函数,最后利用Sigmoid函数输出预测值。
4,回归子网络:回归子网络与分类子网络平行,预测每一个预选框的偏移量,最终输出特征大小为4A×W×W。与当前主流工作不同的是,两个子网络没有权重的共享。
5,Focal Loss:与OHEM等方法不同,Focal Loss在训练时作用到所有的预选框上。对于两个超参数,通常来讲,当 y y y增大时, α \alpha α适当的减小。实验中 y = 2 , α = 0.25 y=2,\alpha=0.25 y=2,α=0.25效果最好。
4, Generalized Focal Loss
论文地址:https://arxiv.org/pdf/2006.04388.pdf
代码地址:https://github.com/implus/GFocal
MMDetection官方收录地址:https://github.com/open-mmlab/mmdetection/blob/master/configs/gfl/README.md
一句话总结:基于任意one-stage 检测器上,调整框本身与框质量估计的表示,同时用泛化版本的GFocal Loss训练该改进的表示,无cost涨点(一般1个点出头)AP
5,GHM,损失函数梯度均衡化机制
论文:https://arxiv.org/pdf/1811.05181.pdf
代码:https://github.com/libuyu/GHM_Detection
GHM主要思想:
GHM做法则是从样本的梯度范数出发,通过梯度范数所占的样本比例,对样本进行动态的加权,使得具有小梯度的容易分类的样本降权,具有中梯度的hard expamle升权,具有大梯度的outlier降权。梯度大说明可学习空间大。
损失函数权重(梯度密度的倒数)
就是把梯度幅值范围(x轴)划分为m个区域,对于落在每个区域样本的权重采取相同的修正方式,类似于直方图。第j个区域范围为 r j r_j rj,用 R j R_j Rj表示落在第j个区域内样本的数量。定义ind(g)表示梯度为g的样本所落区域的序号,那么即可得出新的参数 β i \beta_i βi。样本的梯度密度是训练时根据batch计算出来的,通常情况下batch较小,直接计算出来的梯度密度可能不稳定,所以采用滑动平均的方式处理梯度计算。
S j ( t ) = α ∗ S j ( t − 1 ) + ( 1 − α ) ∗ R j ( t ) S_j^{(t)}=\alpha*S_j^{(t-1)}+(1-\alpha)*R_j^{(t)} Sj(t)=α∗Sj(t−1)+(1−α)∗Rj(t)
G D ( g ) = S i n d ( g ) ∗ M GD(g)=S_{ind}(g)*M GD(g)=Sind(g)∗M
β i = N / G D ( g i ) \beta_i=N/GD(g_i) βi=N/GD(gi)
这里注意M的选取。当M太小的时候,不同梯度模上的密度不具备较好的方差;当然M也不能太大,因为M过大的时候,受限于GPU限制,batch size一般都比较小,此时如果M太大的话,会导致每次统计过于稀疏(分的太细了),异常值对小区间的影响较大,导致训练不稳定。论文根据实验统计,M取30为最佳。
GHM-C分类损失函数
对于分类损失函数,这里采用的是交叉熵函数,梯度密度中的梯度模长是基于交叉熵函数的导数进行计算的,GHM-C公式如下:
L G H M − C = 1 N ∑ i = 1 N β i L C E ( p i , p i ∗ ) = ∑ i = 1 N L C E ( p i , p i ∗ ) G D ( g i ) L_{GHM-C}=\frac{1}{N}\sum_{i=1}^N\beta_iL_{CE}(p_i,p_i^*)=\sum_{i=1}^N\frac{L_{CE}(p_i,p_i^*)}{GD(g_i)} LGHM−C=N1∑i=1NβiLCE(pi,pi∗)=∑i=1NGD(gi)LCE(pi,pi∗)
根据GHM-C的计算公式可以看出,候选样本的中的简单负样本和非常困难的异常样本(离群点)的权重都会被降低,即loss会被降低,对于模型训练的影响也会被大大减少,正常困难样本的权重得到提升,这样模型就会更加专注于那些更有效的正常困难样本,以提升模型的性能。
GHM-R边框回归损失函数
对于回归损失函数,由于原生的Smooth L1损失函数的导数为1时,样本之间就没有难易区分度了,这样的统计明显不合理.论文修改了损失函数 A S L 1 ( d ) = d 2 + u 2 − u ASL1(d)=\sqrt{d^2+u^2}-u ASL1(d)=d2+u2−u,梯度密度中梯度模长是基于修改后的损失函数ASL1的导数进行计算的,GHM-R公式如下:
L G H M − R = 1 N ∑ i = 1 N β i A S L 1 ( d i ) = ∑ i = 1 N A S L 1 ( d i ) G D ( g r i ) L_{GHM-R}=\frac{1}{N}\sum_{i=1}^N\beta_iASL_1(d_i)=\sum_{i=1}^N\frac{ASL_1(d_i)}{GD(gr_i)} LGHM−R=N1∑i=1NβiASL1(di)=∑i=1NGD(gri)ASL1(di)
因为GHM-C和GHM-R是定义的损失函数,因此可以非常方便的嵌入到很多目标检测方法中,论文作者以focal loss(大概是以RetinaNet作为baseline),对交叉熵,focal loss和GHM-C做了对比,发现GHM-C在focal loss 的基础上在AP上提升了0.2个百分点。
总结
- OHEM系列的困难样本挖掘方法在当前的目标检测框架上还是被大量地使用,在一些文本检测方法中还是被经常使用;
- OHEM是针对现有样本并根据损失loss进行困难样本挖掘,Focal Loss和GHM则从损失函数本身进行困难样本挖掘
- 相比Focal loss,GHM是一个动态的损失函数,即随着不同数据的分布进行变换,不需要额外的超参数调整(但是这里其实还是会涉及到一个参数,就是Unit region的数量);此外GHM在降低易分样本权重的同时,对outliner也会有一定程度的降权;
- 无论是Focal Loss,还是基于GHM的损失函数都可以嵌入到现有的目标检测框架中;Focal Loss只针对分类损失,而GHM对分类损失和边框损失都可以;
- GHM方法在源码实现上,作者采用平均滑动的方式来计算梯度密度,不过与论文中有一个区别是在计算梯度密度的时候,没有乘以M,而是乘以有效的(也就是说有梯度信息的区间)bin个数;
- 之前尝试过Focal Loss用于多分类任务中,发现在精度并没有提升;但是我试过将训练数据按照训练数据的原始分布并将其引入到交叉熵函数中,准确率提升了;GHM方法的本质也是在改变训练数据的分布(将难易样本拉匀),但是到底什么的数据分布是最优的,目前尚未定论。
三,目标检测优化使用的Trick
1,数据预处理技巧
图像预处理部分调参的主要目的是对输入数据进行增强,使得网络模型在训练的过程中能更专注于目标特征部分的学习。常用的方式是图像的随机旋转、裁剪以及翻转等方式,这些方式的预处理其本质其实是为了让你的数据集更丰富,让网络能够学习到更多的分布情况,这个网上已经有很多博客了,笔者就不赘述了;另一种调整的trick是在图像上叠加信息,例如在输入数据上增加高斯噪声,椒盐噪声,从而提升网络对有干扰和成像较差情况下的目标检测能力。本文将对图像上叠加信息的调参技巧进行一定的扩展讲解。
- 为什么在原始图像上叠加信息会管用,不会破坏原有的图像信息么?
在图像上叠加信息分成两类,一类是叠加噪声,这种操作的目的是为了让网络能够适应图像质量不佳情况下的图像检测任务,在板端实测的结果,这种叠加噪声的方式也可以一定程度提高网络对输入图像中待检测目标的仿射变换的适应能力。笔者通过在输入图像上叠加一定量的高斯噪声,在Hi3516CV500上完成基于yolov3-tiny的车牌检测任务时,提高了0.5%的精度。
另一类信息的叠加是对尝试对图像上某一特定特征进行增强,该增强的目的是突出该方面的图像特征,使得网络能够首先注意到该种特征并更专注于此类特征的学习,因为这种方式只是对图像中的指定特征或位置有变动,并不会整体上对图像的结构有巨大的改变,所以并不会破坏图像的信息可读性。例如:利用canny算子对图像中的边缘特征进行增强。 - 上面说的两种调参技巧怎么想出来的?
网络学习的是数据中的参数分布,何凯明大神也在retinanet的论文里提到过,**数据的不平衡是影响检测网络性能的主要因素,**而focal loss的提出就是让网络在学习时更专注于漏检和误分的样本。那么我们接着这个思路想,如何使得网络更专注于目标区,从而获得尽量多的价值更高的误捡和漏检样本呢?花朵吸引蜜蜂靠的是自己的香味和更鲜艳的外表,所以我们也要让目标区域更“显眼”,而平时在训练检测网络时,发现对数据集进行标注时,anchor base类算法,目标标注框比实际的物体紧缩框大大概几个像素时得到的检测结果统计精度和定位框的稳定性都会好,那么我们是不是可以认为,对anchor base的检测网络来说,目标物体的边缘也是很重要的,所以就想到了通过canny算子增强边缘的方式来增强训练数据。 - 如何在实际的网络训练应用以上的技巧?
实际使用过程如下:(其他的特征增强方式类似)
1,通过对输入数据的手动查验或自动化统计,确定较好的canny阈值
2,利用阈值对训练样本中10-20个batch的数据进行canny边缘增强
3,增强方式为:原图转灰度提取到的canny边缘所对应的原图像素位置进行对比度增强或直接涂黑。加深程度可以由自定义的超参数alpha来指定。
4,用这10-20个batch的数据进行几个epoch的训练后再换成普通数据进行训练。
2,模型训练参数调整
1.BFEnet特征擦除网络
这个网络是reid方向的,先讲这个是因为,这个特征擦除和上面讲到的噪声本质上有相似的地方,都是通过在训练时遮蔽一部分特征值,来让网络习惯一定量的噪声干扰,从而增强性能。这个技巧可以用在应对有遮挡的场景下的模型。
2.anchor的调整
在yolo的代码里大家肯定都看了,作者是根据你给的数据集里面,标定的目标的长和宽进行k-means的聚类,然后确定在当前这个数据集上的anchor的。我这里的经验就是,我发现有人问过我为啥我只训练一类的检测,然后重新计算的anchor6个或者9个anchor尺寸差的都不大,但是在实际检测的时候,却检测不到东西。我的结论是:对anchor的设计应该是基于模型作者默认的anchor进行微调而不是完全的重新计算。
**原因:**大家都知道,yolov3来说,输出是三个特征图,分别对应小目标,中目标和大目标。比如我们要检测的目标在图像中占比我们人眼感觉应该是比较大的,然后我们统计的框也都是比较大的尺寸,但是在实际训练的时候,并不是说大目标就一定由yolov3的最初设计的大目标输出层输出的。很可能就是由中间目标层输出的,而因为anchor的设计过大,导致训练的网络不收敛的有之,明明收敛了,却检测不到目标的情况也有之。
解决办法:在设计anchor的时候,首先统计目标框的分布,然后进行聚类,聚类后替换或修改原有的9个anchor中和你计算的anchor相近的几个原有的anchor值。
然后再训练,如果框还是不够紧缩,再对某几个框进行精调就可以了,核心思路就是:anchor的分布也要满足对全集的稀疏覆盖而不仅仅是你的当前数据集。
3.后处理优化
后处理的优化部分严格来说不算是网络训练的trick了,应该是部署的trick,比如海思的NPU部署的时候,会限制比较大的pool核,所以最好训练的时候就把大的pooling切换为几个小的连续pooling,实测虽然理念上两者应该是差不多的,但是实际上还是差了0.3%的精度。(指的是直接多层的pooling转换到板子和训练时是一个大的pooling,到转换时候再改结构成几个小的pooling)
nms(非极大值抑制):数据集有遮挡,可能两个离的比较近的,nms就把有遮挡的那个小目标去掉了。这部分分享一个小技巧就是,你在算nms的时候,也关注一下两个框的中心点距离,可以设置中心点距离超过多少的两个框,不做nms。这样就能避免nms的一部分武断删除检测结果bbox。
4.大规模数据训练的一个小技巧:warm up
为啥同样的模型,用比较少的数据训练的时候很快到了97%的MAP,但是换300w的大数据集的训练以后,卡在93%上不去了。这里面有一个技巧叫warm up,也就是说在大数据下训练模型的时候,可以先从大数据集上取一部分数据训练模型,然后以这个训练的模型为预训练模型,在大数据集上,增大batch_size再进行训练,至少没卡在93%这个问题上了。
5.学习率手动调整
我们训练的时候,一般都会设置学习率的衰减,有很多的方式,**按已迭代步长的,按当前损失值的,按训练集当前损失值和测试集计算的损失值的gap差值做修正项的。**我这里提到的技巧就是比如以步长调整学习率为例,什么时候可以靠自动化的修正学习率,什么时候要手动调整一下。
我们在训练模型的时候,一般都会关注损失函数变化曲线图,在曲线图中,数据集的稀疏程度能通过损失曲线的震荡情况有一定的反映,如果有个别的跳点,多为数据集中的坏数据(标记错误数据),当我们的损失图呈现为震荡–阶跃–在另一个损失值附近震荡时,就要注意了,此时多半是因为你的数据集在做打乱的时候数据并没有打的很散,可以在这个位置先停止训练并记录当前状态,再降低学习率,继续训练,等训练数据再次开始恢复之前的震荡位置时,再恢复学习率训练。
这样操作的原因是为了避免在参数中引入过大的噪声,**噪声分两种,一种就是错误的数据,比如背景啊,像目标但是不是目标的东西,还有就是多类别训练的时候,对每个类别来说,其余类别也算是噪声的一种。**所以采用要么把数据集弄好(这个很难,我也没看过谁的文章里真的能说清把训练集弄好是啥样的),要么加大batch,要么就训练时候注意。
四,小目标检测常用解决方案
在深度学习目标检测中,特别是人脸检测中,小目标、小人脸的检测由于分辨率低,图片模糊,信息少,噪音多,所以一直是一个实际且常见的困难问题。不过在这几年的发展中,也涌现了一些提高小目标检测性能的解决手段,本文对这些手段做一个分析、整理和总结。
传统的图像金字塔和多尺度滑动窗口检测
最开始在深度学习方法流行之前,对于不同尺度的目标,大家普遍使用将原图build出不同分辨率的图像金字塔,再对每层金字塔用固定输入分辨率的分类器在该层滑动来检测目标,以求在金字塔底部检测出小目标;或者只用一个原图,在原图上,用不同分辨率的分类器来检测目标,以求在比较小的窗口分类器中检测到小目标。
在著名的人脸检测器MTCNN(https://arxiv.org/abs/1604.02878)中,就使用了图像金字塔的方法来检测不同分辨率的人脸目标。
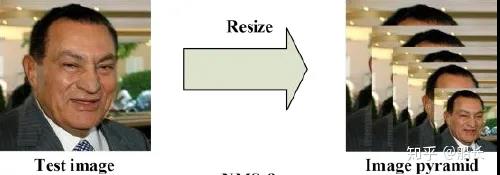
不过这种方式速度慢(虽然通常build图像金字塔可以使用卷积核分离加速或者直接简单粗暴地resize,但是还是需要做多次的特征提取呀),后面有人借鉴它的思想搞出了特征金字塔网络FPN(空洞卷积神经网络),它在不同层取特征进行融合,只需要一次前向计算,不需要缩放图片,也在小目标检测中得到了应用。
简单粗暴可靠的数据增强
深度学习的效果某种意义是靠大数据喂出来的,小目标检测的性能同样也可以通过增加训练集中小目标的种类和数量来提升。 19年论文:Augmentation for small object detection(https://arxiv.org/abs/1902.07296)
1.OverSampling

在图片内用分割的Mask抠出小目标图像再使用复制粘贴的方法。(也加上一些旋转和缩放,注意不要遮挡到别的目标)
特征融合的FPN
不同阶段的特征图对应的感受野不同,它们表达的信息抽象程度也不一样。浅层的特征图感受野小,比较适合检测小目标;深层的特征图感受野大,适合检测大目标。所以,有人提出将不同阶段的特征融合起来,提升目标检测的性能,这就是特征金字塔网络FPN:https://arxiv.org/abs/1612.03144
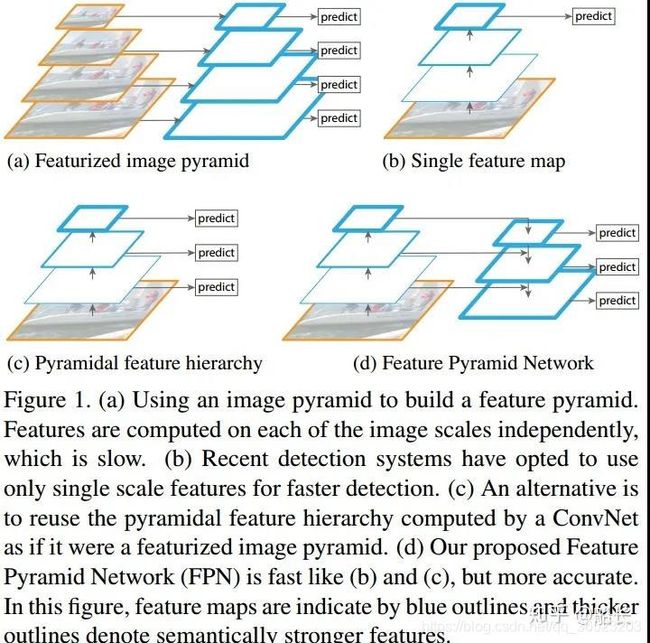
在人脸领域,基本上性能好一点的方法都是用了FPN的思想,其中比较有代表性的有RetinaFace: Single-stage Dense Face Localisation in the Wild(https://arxiv.org/pdf/1905.00641.pdf)
多尺度检测
另外一种思路:既然可以在不同分辨率特征图做融合来提升特征的丰富度和信息含量来检测不同大小的目标,那么自然也有人会进一步地猜想,如果只用高分辨率的特征图(浅层特征)去检测小脸;用中间分辨率的特征图(中层特征)去检测大脸;最后用地分辨率的特征图(深层特征)去检测小脸。比如人脸检测中的SSH(https://arxiv.org/pdf/1708.03979.pdf)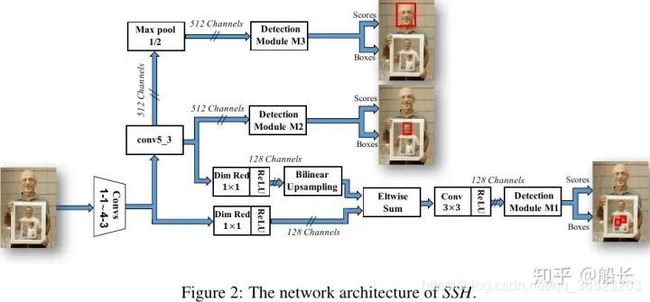
在YOLOv3后也同样采用了该思想。
合适的训练方法SNIP,SNIPER,SAN
机器学习的重要观念:**模型预训练的分布要尽可能地接近测试输入的分布。所以,在大分辨率(比如常见的224 x 224)下训练出来的模型,不适合检测本身是小分辨率再经放大送入模型的图片。如果是小分辨率的图片做输入,应该在小分辨率的图片上训练模型;再不行,应该用大分辨率的图片训练的模型上用小分辨率的图片来微调fine-tune;最差的就是直接用大分辨率的图片来预测小分辨率的图(通过上采样放大)。但是这是在理想的情况下的(训练样本数量、丰富程度都一样的前提下,但实际上,很多数据集都是小样本严重缺乏的),所以放大输入图像+使用高分率图像预训练再在小图上微调,在实践中要优于专门针对小目标训练一个分类器。多尺度训练

下图示意的是SNIP训练方法,训练只训练合适尺寸的目标样本,只有真值的尺度和ANchor的尺度接近时来训练检测器,太小太大的都不要,预测时输入图像多尺度,总有一个尺寸的Anchor是合适的,选择那个最合适的尺度来预测。对R-FCN(https://arxiv.org/abs/1605.06409)提出的改进主要有两个地方,一是多尺寸图像输入,针对不同大小的输入,在经过RPN网络时需要判断valid GT和invalid GT,以及valid anchor和invalid anchor,通过这一分类,使得得到的预选框更加的准确;二是在RCN阶段,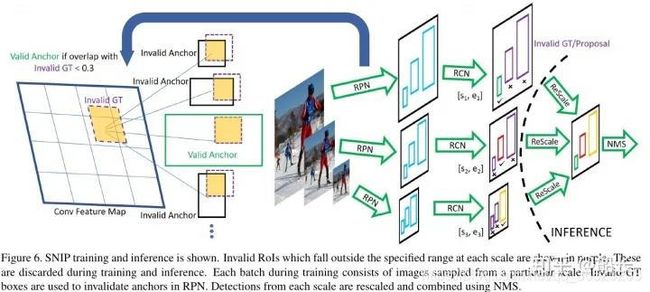
**,最后使用NMS来得到最终结果。
更稠密的Anchor采样和匹配策略S3FD,FaceBoxes
在前面Data Augmentation部分已经讲了,复制小目标到一张图的多个地方可以增加小目标匹配的Anchor框的个数,增加小目标的训练权重,减少网络对大目标的bias。同样,反过来想,如果在数据集已经确定的情况下,我们也可以增加负责小目标的Anchor的设置策略来让训练时对小目标的学习更加充分。例如人脸检测中的FaceBoxes(https://arxiv.org/abs/1708.05234)其中一个Contribution就是Anchor densification strategy,Inception3的anchors有三个scales(32,64,128),而32 scales是稀疏的,所以需要密集化4倍,而64 scales则需要密集化2倍。
在S3FD
http://openaccess.thecvf.com/content_ICCV_2017/papers/Zhang_S3FD_Single_Shot_ICCV_2017_paper.pdf)人脸检测方法中,则用了Equal-proportion interval principle来保证不同大小的Anchor在图中的密度大致相等,这样大脸和小脸匹配到的Anchor的数量也大致相等了。
另外,对小目标的Anchor使用比较宽松的匹配策略(比如IoU > 0.4)也是一个比较常用的手段。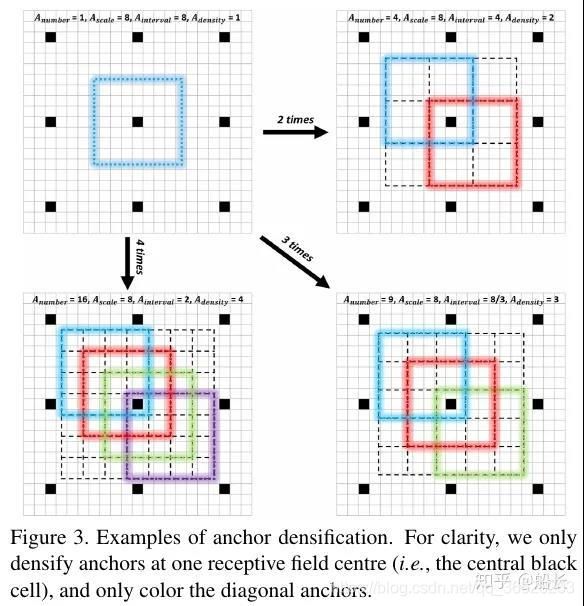
在做重叠目标检测时,也会在非极大值抑制算法中,降低iou的阈值,或者不直接删除检测框,而是降低置信度。
先生成放大特征再检测的GAN
Perceptual GAN使用了GAN对小目标生成一个和大目标很相似的Super-resolved Feature(如下图所示),然后把这个Super-resolved Feature叠加在原来的小目标的特征图(如下下图所示)上,以此增强对小目标特征表达来提升小目标(在论文中是指交通灯)的检测性能。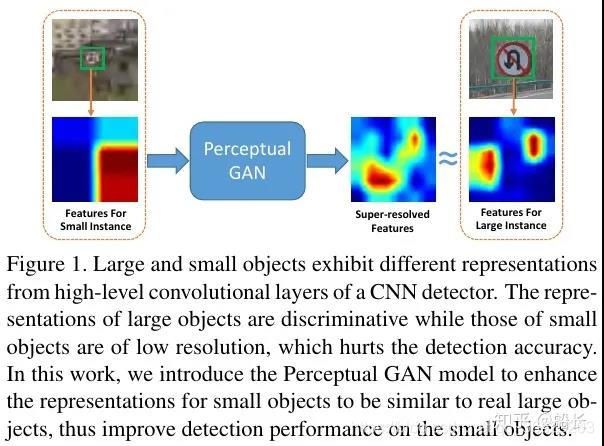

利用Context信息的Relation Network和PyramidBox
小目标,特别是像人脸这样的目标,不会单独地出现在图片中(想想单独一个脸出现在图片中,而没有头、肩膀和身体也是很恐怖的)。像PyramidBox(https://arxiv.org/abs/1803.07737)方法,加上一些头、肩膀这样的上下文Context信息,那么目标就相当于变大了一些,上下文信息加上检测也就更容易了。
这里顺便再提一下通用目标检测中另外一种加入Context信息的思路,Relation Networks(https://arxiv.org/abs/1711.11575)虽然主要是解决提升识别性能和过滤重复检测而不是专门针对小目标检测的,但是也和上面的PyramidBox思想很像的,都是利用上下文信息来提升检测性能,可以归类为Context一类。
五,目标检测多模型集成方法
不同的集成方式
- OR方法:如果一个框是由至少一个模型生成,就会考虑它。
- AND方法:如果所有模型产生相同的框,则认为是一个框(如果IOU>0.5)
- 一致性方法:如果大多数模型产生相同的框,则认为一个框,即如果由m个模型,(m/2+1)个模型产生相同的框,则认为这个框有效。
- 加权融合:这是一种替代NMS的新方法,并指出其不足之处。
检测框加权融合
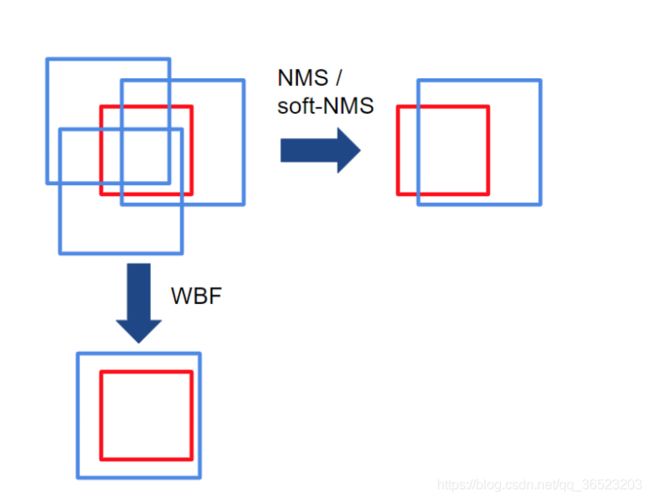
在NMS方法中,如果框的IoU大于某个阈值,则认为框属于单个物体。因此,框的过滤过程取决于这个单一IoU阈值的选择,这影响了模型的性能。然而,设置这个阈值很棘手:如果有多个物体并排存在,那么其中一个就会被删除。NMS丢弃了冗余框,因此不能有效地从不同的模型中产生平均的局部预测。
NMS和WBF之间的主要区别是,WBF利用所有的框,而不是丢弃它们。在上面的例子中,红框是ground truth,蓝框是多个模型做出的预测。请注意,NMS是如何删除冗余框的,但WBF通过考虑所有预测框创建了一个全新的框(融合框)。
六.对Anchor的优化
1.Anchor refinement module (ARM)
RefineDet中使用的ARM模块对Anchor进行微调,然后将微调后的anchor送到ODM模块中进一步预测。这样anchor就变成了一个变量,而不是固定的。
ARM是One-Stage检测器中使用的类似RPN模块,[Shifeng Zhang, Longyin Wen, Xiao Bian, Zhen Lei, and Stan Z Li. Single-shot refinement neural network for object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2018]首先提出的。它在多尺度检测框架下,在每个 detection source layer上附加两个卷积核。ARM的主要目的是为每个anchor分配背景/前景分数和预测调整的位置。利用二进制分类分数筛选出负样本,并将细化的anchor发送到最终的目标检测模块(ODM),与SSD中的检测器头完全相同。为了更好地分析ARM对探测器的影响,首先给出了探测器头的边界框回归和分类的定义。