算法刷题重温(一):二叉树的 前中后层序 遍历的写法总结(树专题)
1. 写在下面
最近又重新开始刷算法题,这次刷题和之前不太一样, 之前刷题的时候,由于对整体宏观没有把握住,所以大多是以框架思维为主,按照从基本的数据结构到算法这样的专题思路进行刷题, 每学一个地方,就要先整理相关理论,然后对应的一些题目刷一遍。 这样的好处是长期下来会形成一个知识框架,后面复刷的时候会很容易梳理总结。 缺点就是太费时间, 我花了很长的一段时间(从上年9月开始吧),到现在刚整理到一半, 而现在转眼就到了新的一年的快二月份了, 感觉这个思路进行的太慢了, 这样搞下去根本看不到全貌了,所以这次重新一种思路重新刷, 根据第一遍,大体上知道了重点和常考题型, 所以这一次的话就先以重点切入,从牛客和剑指offer开始(面向面试刷题), 这个过程(只要框架有的)就不梳理,直接刷相关题目,如果框架没有的再反推到我的第一遍框架进行补充,这个好处是速度会提上来,但是缺点是不好成体系,即使基于第一遍的框架也不太容易记住思路, 所以我觉得比较好的方式就是这两种方式结合起来,进行思想提炼。 所以在第二遍的过程中,通过写博客的方式提炼出各个部分最关键的一些思路,代码来应对面试,这次没有第一遍的那么全(各种思路解法会过一遍),重点是分类梳理最底层的思维逻辑代码,形成类似于我自己的一套模板性的东西。
这次开刷从树结构开始,因为树结构的重要性不言而喻,以树为中心刷,既能带动链表,又能开启图,算法涉及递归,回溯,动规,贪心,分治等,所以这个结构巨重要。 而树里面二叉树又是重中之重, 所以这篇文章从二叉树的遍历开始 - 复习二叉树的前中后序的递归和非递归代码, 层序遍历之BFS, 这几个代码非常非常重要。牢牢的掌握这7个框架, 就可以搞掉二叉树这里大部分的题目(大约30道)。
这个是牛客上的二个题目
- 分别按照二叉树先序,中序和后序打印所有的节点
- 给定一个二叉树,返回该二叉树层序遍历的结果,(从左到右,一层一层地遍历)
用这两个中规中矩题目来走一遍核心代码, 如果打通了这个逻辑,以不变应万变,可以解决树这块的很多内容。下面开始默写
2. 前序遍历
前中后的递归写法都比较简单,但不能光记这个,非递归也需要会默写,非递归可以更好的帮助我们走遍历过程,另一方面一些变形题目可能涉及到一些中间过程,非递归处理起来会容易些。
2.1 递归写法
不解释,直接上代码。
pre_res = []
def PreOrder(root, pre_res): # 根 和存储前序遍历结果的
if not root:
return
# 访问或处理根的逻辑
pre_res.append(root.val)
# 左节点存在,访问
if root.left:
PreOrder(root.left, pre_res)
# 右节点存在,访问
if root.right:
PreOrder(root.right, pre_res)
# 不用返回结果,因为上面的pre_res是全局变量
# 递归前序遍历
PreOrder(root, pre_res)
2.2 非递归写法
这里写的时候,脑海中也要这样的流程, 首先既然是递归实现的,我们就需要手动维护个栈, 这样按照前序遍历: 根 -> 左节点 -> 右节点的访问顺序, 当我们拿到根节点的时候, 需要先访问,然后入栈(为了将来访问右孩子), 然后去他的左孩子, 进行同样的逻辑操作。 当到了最左边没有左孩子的时候, 开始出栈顶部元素,然后去访问右孩子。 有了这样一个流程,我们转换成代码:
pre_res = []
def PreOrder(root, pre_res):
# 栈来
stack = []
# 开始判断
while root or stack: # 这个写法比较简单,前中后都可以用
# 如果当前节点不空, 访问,入栈,找左
while root:
# 访问或者处理根的逻辑
pre_res.append(root.val)
stack.append(pre_res)
root = root.left
# 上面循环退出,说明root此时是空,即到了最左边,此时栈顶就是最左边的叶子节点,出栈,访问右孩子
root = stack.pop()
root = root.right
# 不用返回结果,因为上面的pre_res是全局变量
# 非递归前序遍历
PreOrder(root, pre_res)
上面这两个模板虽然很简单,但是功能很强大, 一些变体,都可以基于这两个模板处理一些中间结果的。这次刷题如果遇到了,会统一整理上来。
3. 中序遍历
3.1 递归写法
不解释,直接上代码
in_res = []
def inorder(root, in_res):
if not root:
return
# 先访问左子树
if root.left:
inorder(root.left, in_res)
# 访问根 或者处理根逻辑
in_res.append(root.val)
# 访问右子树
if root.right:
inorder(root.right, in_res)
# 中序递归遍历
inorder(root, in_res)
3.2 非递归写法
这里脑海中要有这样的定式:
- 非递归手动维护栈
- 左孩子 -> 根 -> 右孩子
- 当我们拿到root, 我们要先入栈,然后找左孩子,到最左边之后,访问,然后去他的右孩子
把上面的流程,翻译成代码:
in_res = []
def in_order(root, in_res):
# 栈来
stack = []
while root or stack:
# 去找他左孩子
while root:
stack.append(root)
root = root.left
# 但root为空,说明到了最左边了, 栈顶元素就是最左边的叶子,出栈访问
root = stack.pop()
# 访问或处理逻辑
in_res.append(root.val)
# 去右孩子
root = root.right
# 中序遍历非递归
inorder(root, in_res)
4. 后序遍历
4.1 递归写法
不解释,直接上代码
post_res = []
def postorder(root, post_res):
if not root:
return
if root.left:
postorder(root.left, post_res)
if root.right:
postorder(root.right, post_res)
# 访问根逻辑
post_res.append(root.val)
# 后序递归遍历
postorder(root, post_res)
4.2 非递归写法
这个相比上面两个来说稍微麻烦一点, 但只要判别出当我们到了某个根节点之后,我们是从左边回去的,还是从右边回去的,其实就可以了。 所以下面的一个定式:
- 手动维护栈
- 左孩子 -> 右孩子 -> 根
- 这里需要判断当前root是从他左孩子还是右孩子处返回来的,如果是左孩子返回来的,需要去访问右孩子,如果是右孩子返回来的, 需要访问root
- 这里的一个处理技巧就是往左找的时候,我们不是找最左边那个了,而是找第一个需要访问的叶子节点, 有了第一个节点,后面就好说了,先访问这个节点,然后判断它是它父亲的左孩子还是右孩子(它父亲在栈里面),如果是左孩子, 那么去访问它父亲的右孩子, 如果是右孩子, 当前置为空,下一轮直接访问它父亲正好
上面这个题目阿里曾经有个面试题考过,就是仅仅用栈来实现后序的非递归遍历,不能借助其他结构。下面我们写代码吧:
post_res = []
def post_order(root, post_res):
# 栈来
stack = []
# 判断
while root or stack:
# 找第一个叶子节点,这里看小技巧
while root:
stack.append(root)
root = root.left if root.left else root.right # 关键就在这里
# 这样root为空的时候,栈顶就不是最左边了,而是第一个应该访问的叶子,出栈访问它
root = stack.pop()
post_res.append(root.val)
# 下面判断是它父亲的左节点还是右节点
if stack and stack[-1].left == root: # 是它父亲的左孩子
root = stack[-1].right # 直接访问它父亲右孩子
else:
root = None # 否则,说明这个分支完事了,下轮直接访问它父亲即可
# 后序非递归
postorder(root, post_res)
这样,前中后的递归和非递归梳理完毕, 这里的非递归算法中规中矩,虽然这三个有点小小的不统一,但完全是模拟了遍历过程。 这样写可以真正的去掌握思想, 虽然看到题解里面有很多写法都把前中后的非递归给统一了起来,类似递归的形式(我第一轮整理过),但这次发现那种写法虽然好记一点,但已经迷失了遍历的过程(尤其是后序,没有这种最后访问根的感觉了), 这样可能不利于迁移到别的题目上去,也就是仅仅停留在这样的遍历过程,一旦遇到变形,处理中间的某个逻辑的时候,可能就乱了套。所以这里我不打算采用那种方式了,中规中矩,掌握核心思想才是王道。
5. 层序遍历
树的层序遍历属于bfs的范畴了,bfs两个重大应用场景:层序遍历和最短路径。
这里首先定式, 提到bfs先想到队列, dfs先想到栈。关于层次遍历是怎么回事,这里不解释, 这里整理两个模板:
baseline模板, 这个就是传统的bfs遍历模板,巨重要:
def bfs(root):
if not root:
return
d = collections.deque([])
d.append(root)
while d:
root = d.popleft()
if root.left:
d.append(root.left)
if root.right:
d.append(root.right)
但这个无法区分队列中的节点来自哪一层。所以这个还不能直接拿来做二叉树的层序遍历。
层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层,也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组,无法区分每一层。
所以层序遍历的话, 我们需要在每一层遍历开始前,先记录队列中的结点数量 n n n(也就是这一层的结点数量),然后一口气处理完这一层的 n n n个结点。上代码:
from collections import deque
level_res = []
def level_order(root, level_res):
if not root:
return level_res
# 队列来
d = dequne([root])
while d:
# 先统计当前层的节点个数
size = len(d)
# 记录当前层的几点结果
level_tmp = []
# 遍历当前层所有节点
for _ in range(size):
root = d.popleft()
# 节点处理逻辑
level_tmp.append(root.val)
# 左节点存在,入队
if root.left:
d.append(root.left)
# 右节点存在,入队
if root.right:
d.append(root.right)
# 把当前层结果加入总结果
level_res.append(level_tmp)
# 层序遍历
level_order(root, level_res)
有了这个模板, 像后面的层序遍历题目统统一网打尽。
下面开始展示这7个框架的威力。
6. 遍历这块题目梳理总结
6.1 前序遍历
- LeetCode257: 二叉树的所有路径: 完全的前序遍历递归, 修改中间逻辑, 保存路径, 有点回溯的味道了
- LeetCode 226: 翻转二叉树: 前序遍历的递归方式, 修改当前层的处理逻辑即可,这个题目在第二篇二叉树构造那里有整理
- LeetCode 129: 求根到叶子节点数字之和(牛客也有): 前序遍历递归方式, 只不过函数中需要额外加一个参数
single_sum来统计每条路径上的和,当然不是简单的加和,每下去一层,要乘10,处理逻辑的核心代码single_sum = single_sum * 10 + root.val, 如果是叶子的时候, 加完之后更新全局的和即可。 - LeetCode113(剑指offer34):路径总和II, 牛客): 上面这个题的变式题目, 只要能求出每条路径的和来,只需要在上面叶子判断里面加一个判断, 如果是
sum,更新结果即可。当然,每层的处理逻辑那里还需要保存每一步的路径值, 再加一个path参数, 这个当然有点回溯的味道了, 因为path那个地方不能加在当前层处理逻辑哪里, 要加到下一层的参数那,否则就需要回溯

- Leetcode112: 路径总和, 牛客也有:这个是上面的简单变式, 不需要输出路径,只需要判断有没有路径即可。 所以依然是完全前序递归模板, 不用保存每一条路径, 对比中就可以发现底层的思维逻辑才是最关键的,框架下面, 很多东西都是一致的。
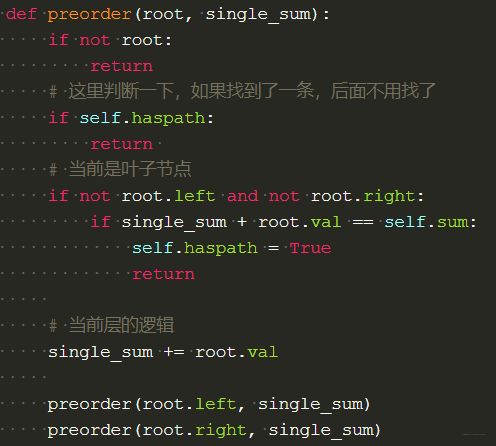
- Leetcode404: 左叶子之和: 前序遍历的递归模板, 只需要改当前层的处理逻辑, 也就是判断出左叶子节点来:
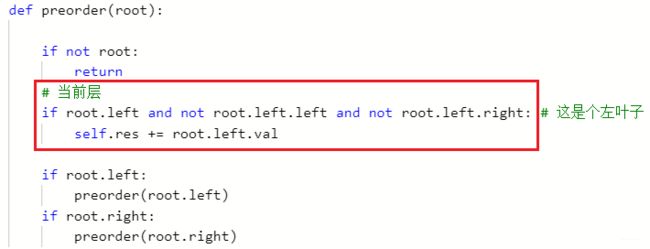
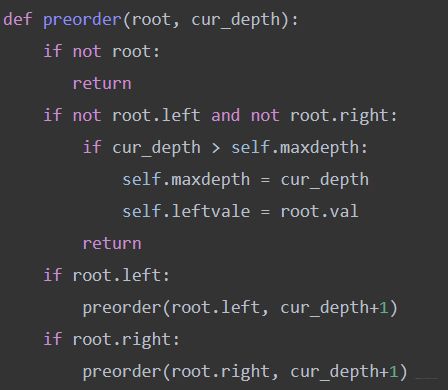
- LeetCode513: 找树左下角的值: 这个题目也是完全的前序遍历模板,只不过参数上需要加一个cur_depth来记录叶子节点所在的层数,因为最左下角的值是深度最大的叶子节点, 得需要体现出深度最大来。 所以当前层的处理逻辑是如果遇到了叶子,就需要判断,然后更新最大深度和叶子几点的值。这个也隐藏着回溯。
6.2 中序遍历
中序遍历这里能够体现其强大的就是结合着二叉搜索树来看, 因为二叉搜索树的中序遍历是递增的, 这里通过LeetCode98: 验证二叉搜索树这个题目,就能看到中序遍历的强大之处。
中序遍历一遍二叉树, 如果遍历途中发现当前节点的值比前面节点的值小, 那么就不是一棵二叉搜索树。递归框架拿过来, 然后修改当前层的逻辑
class Solution:
def __init__(self):
self.pre = float('-inf')
def isValidBST(self, root: TreeNode) -> bool:
if not root:
return True
# 判断左子树是否二叉搜索树
if not self.isValidBST(root.left):
return False
# 当前层的处理逻辑,如果前面那个数大于当前数,不是
if root.val <= self.pre:
return False
self.pre = root.val
return self.isValidBST(root.right)
这个题目用中序遍历的非递归框架感觉更好看一些,完全非递归框架, 修改当前节点的处理逻辑:
def isValidBST(self, root: TreeNode) -> bool:
stack = []
pre = float('-inf')
while root or stack:
# 去找最左边的节点
while root:
stack.append(root)
root = root.left
# 出栈栈顶元素,看看是否小于它前面的节点值,然后更新前面的节点值
root = stack.pop()
# 当前节点的处理逻辑
if root.val <= pre:
return False
pre = root.val
root = root.right
return True
这两个框架不仅能判断是否是二叉搜索树, 还能在二叉搜索中, 直接找最小的第K个元素LeetCode230. 二叉搜索树中第K小的元素,也是只需要修改当前节点的处理逻辑
class Solution:
def isValidBST(self, root: TreeNode, k:int) -> int:
stack = []
while root or stack:
# 去找最左边的节点
while root:
stack.append(root)
root = root.left
root = stack.pop()
k -= 1
if k == 0:
return root.val
# 去右边
root = root.right
递归更简洁, 也是只需要修改当前逻辑
class Solution:
def __init__(self):
self.res = None
self.k = None
def kthSmallest(self, root: TreeNode, k: int) -> int:
self.k = k
def inorder(root):
if not root: return
inorder(root.left)
if self.k == 0: return # 这里需要剪枝
self.k -= 1
if self.k == 0:
self.res = root.val
inorder(root.right)
inorder(root)
return self.res
不过这种需要一个全局的变量来控制。
类似的变式题目: 剑指 Offer 54. 二叉搜索树的第k大节点, 这个题目也是中序遍历的非递归框架,只不过这个比较巧妙的是反着用了,也就是先遍历右,再去遍历左,这时候才能找第k大。
class Solution:
def kthLargest(self, root: TreeNode, k: int) -> int:
stack = []
while root or stack:
while root: # 先去右
stack.append(root)
root = root.right
root = stack.pop()
k -= 1
if k == 0:
return root.val
# 这时候去左
root = root.left
当然二叉搜索中的这种第K大和第K小还有种比较清晰的思路,就是先中序遍历存到数组,这是个递增序列,然后直接返回相应的数也行,只不过时间会花费的多一些。
可以看到, 底层思维框架的重要性, 一套框架,瞬间搞定了二叉搜索树三个题目, 还没爽完? 下面继续爽,哈哈。
- LeetCode530: 二叉搜索树的最小绝对差: 完全二叉树中序遍历非递归, 修改当前的处理逻辑

- LeetCode501: 二叉搜索中的众数: 完全中序遍历非递归框架,修改当前处理逻辑, 用一个字典统计每个数出现的次数,最后遍历字典,返回众数。 这是我第一次a的代码,面试来不及,就用这款,这个没法体现中序遍历的二叉搜索递增的优势。
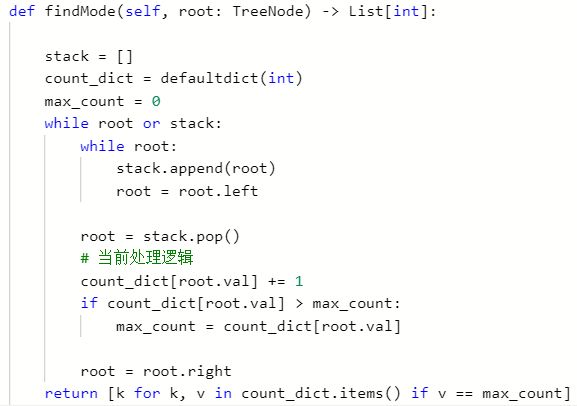
python里面用字典统计个数的时候,最好用defaultdict(int)字典, 如果键没在字典里会自动添加且默认0, 在collections包里面。但如何体现中序递增的优势呢? 这个之前也想过,就是用边统计边更新的思路统计,但这样只能找出一个众数,找不出集合来。 于是看了波题解,发现了新思路,依然是完全的中序遍历非递归框架,通过修改处理逻辑,可以遍历一次找出所有的众数。 这种思路学习一下:
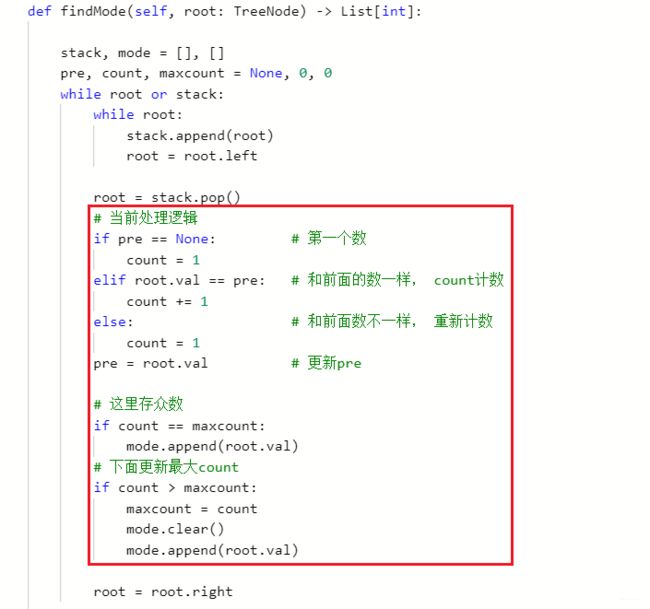
- LeetCode538: 把二叉搜索树转换为累加树: 完全的中序遍历非递归模板, 修改当前节点的处理逻辑, 并且这个需要先去右边,然后去左边。 当前的逻辑里面需要进行累加操作。

6.3 后序遍历
-
leetcode 236, 剑指offer 68, 牛客: 二叉树的最近公共祖先:完全后序遍历的非递归模板,处理当前逻辑那块保存p和q的祖先
-
Leetcode110. 判断是否平衡二叉树:后序遍历的递归方式, 自底向上, 这里还应该明白的一点是二叉树深度和二叉树高度其实不是一个东西的, 看了人家的题解才发现这个问题, 可以参考这个题解, 求深度适合用前序遍历, 而求高度适合用后序遍历
-
LeetCode 226: 翻转二叉树: 后序遍历的递归方式, 修改当前层的处理逻辑即可
-
LeetCode 104: 二叉树的最大深度: 求一棵树高度的代码, 后序遍历的递归模板,每棵树需要返回高度值。有了这个题,再去拓展,就是N叉树的最大高度思路, 需要修改中间这个,毕竟N叉树要遍历分叉。最大深度就是求根节点的高度
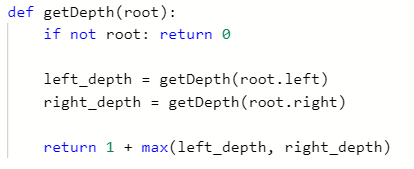
-
LeetCode559: N叉树的最大深度: 这个和上面这个基本上一模一样, 把上面的这个子树改成遍历节点孩子的操作即可。

-
LeetCode111: 二叉树的最小深度: 这个题目后序遍历也可以搞定, 需要改返回结果时的逻辑, 由于这里是最小, 那么返回结果的时候,如果两个子树都不是空, 那么最小深度为左右子树的最小深度+1, 但是这里要注意如果其中有一个为空, 最小深度为不为空的那个深度+1, 这是和求最大深度不一样的地方

可以发现,这种框架式的底层思维,只需要改一小部分代码就能解决很多问题。
-
Leetcode222: 完全二叉树的节点个数: 完全的后序遍历模板, 和最大深度的一样,也需要返回值。
从上面发现了一个类似规律的小问题, 发现绝大多数后序遍历的题目都得需要返回值, 也就是先左右,后中, 然后跟着中的处理逻辑的时候有返回值。 而前序遍历那里一般递归函数里面不用返回值,一般都是全局遍历进行保存。当然,也不一定,这里也拿代码随想录里面总结的一句话作为参考:
如果需要搜索整颗二叉树,那么递归函数就不要返回值,如果要搜索其中一条符合条件的路径,递归函数就需要返回值,因为遇到符合条件的路径了就要及时返回。
感觉还是看具体的需求吧,这句话说的也不是那么绝对。
6.4 层序遍历
- LeetCode107: 二叉树的层序遍历II: 完全的层序遍历模板,这里改成了自底向上输出遍历结果, 最后结果逆序输出即可
- LeetCode513: 找树左下角的值: 和上面这个一模一样,完全的层序遍历模板,只不过返回的时候是最后一层的第一个值即可。当然,还有层序遍历的简单思路,就是简单的那个层序遍历模板, 每一层从右向左,这样最后一个节点正好是最左边。 如果用DFS的话,需要加一个深度参数进行标识,找最大深度的第一个叶子
- LeetCode103: 之字形层序遍历: 完全是层序遍历模板,添加结果时候左右加一标识
- LeetCode111: 二叉树的最小深度: 完全层序遍历模板, 出队后的处理逻辑那块判断是否遇到了叶子,如果是返回当前深度, 同样后序遍历也可以搞定
- LeetCode 104: 二叉树的最大深度: 完全层序遍历模板, BFS求树高的思路,这个后序遍历也可以解决
- LeetCode515: 每个树行中找最大值: 完全层序遍历模板,出队处理逻辑那里保存最大或者最小值
- LeetCode199:二叉树的右视图: 完全层序遍历模板, 出队处理逻辑那里保存每一层最右边的那个值即可
- LeetCode515:每个树行中找最大值: 完全层序遍历模板, 出队处理逻辑那里保存每一层的最大值即可
- LeetCode637: 计算二叉树每一层的平均值: 完全层序遍历模板, 出队逻辑那里保存每一层的节点值,每一层结束后保存平均结果到最终结果即可
- LeetCode429: N 叉树的层序遍历: 完全层序遍历模板, 但是这里由于是N叉树了,这里需要修改入队操作那里, 不是root.left和root.right入队了, 而是遍历root.children, 把各个节点入队
- LeetCode116: 填充每个节点的下一个右侧节点指针: 完全层序遍历模板, 出队处理逻辑那里需要修改节点的next指针
- LeetCode117: 填充每个节点的下一个右侧节点指针II: 这个如果使用完全层序遍历模板, 完不完美二叉树通吃, 所以这个和上面这个代码一模一样就能A掉。
- LeetCode 226: 翻转二叉树: 层序遍历的简介模板,出队的那里修改逻辑
- 剑指offer28: 对称二叉树(牛客高频): 这个题目可以使用层序遍历的非递归解法搞掉,还是完全层序遍历模板,只不过处理出队处理逻辑的地方需要判断一下是否是空值,不是空值直接加入当前层列表,否则加入#标记。因为这个题目空值也得加入到队列。 在处理完一层之后, 要判断当前层的这个列表是不是对称即可。 因为如果是对称二叉树, 那么每一层肯定是对称的才行。
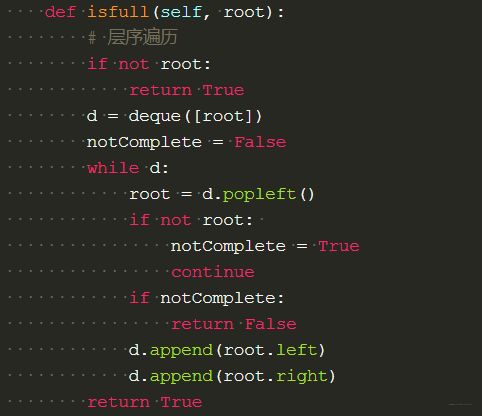
- 牛客: 判断一棵树是否是完全二叉树: 完全二叉树可以使用简单的层序遍历框架, 出队逻辑那里,遇到一个空值退出循环。 在循环外遍历队列中元素,如果发现还有不空的元素,那么就不是完全二叉树。 当然这里记录学习到的一种巧妙方式, 这里的continue用的巧妙。