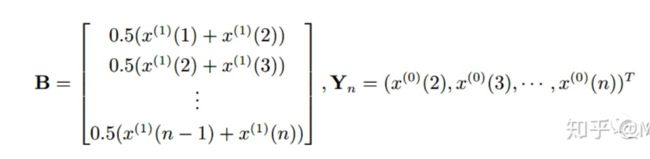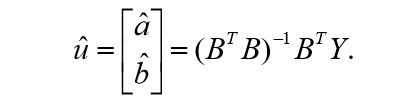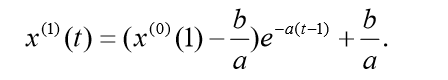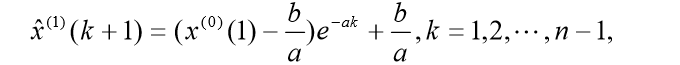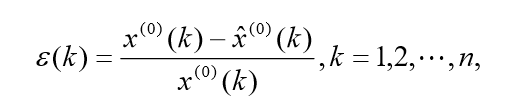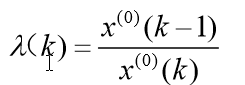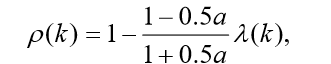数学建模_灰色关联分析和预测_2020_9_11
1:灰色关联度分析 GRA(Grey Relation Analysis )
灰色预测的概念:
白色系统是指一个系统的内部特征是完全已知的
黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系加以研究
灰色系统内部信息一部分是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系
灰色关联度分析
对系统进行因素分析,这些因素那些对系统是主要的,那些是次要的,那些需要发展,那些需要抑制。那些是潜在的,那些是明显的。因素间关联性如何,关联程度如何量化是系统分析的关键。
灰色关联度分析的步骤
第一步:确定分析数列。
参考数列(母序列):反映系统行为特征数据序列
Y = Y(k) k=1,2...n
比较数列(子序列): 影响系统行为的因素组成的数据序列
k=1,2,...n i=1,2,...m
第二步,变量的无量纲化
由于系统中各因素列中的数据可能因量纲不同,不便于比较或在比较时难以得到正确的结论。因此在进行灰色关联度分析时,一般都要进行数据的无量纲化处理。主要有下两种方法
初值化处理: k=1,2,...n i=1,2,...m
均值化处理: k=1,2,...n i=1,2,...m
第三步,计算关联系数:
其中 ρ为分辨系数,0<ρ<1。若ρ越小,关联系数间差异越大,区分能力越强。通常ρ取0.5
第四步,计算关联度
第五步,排序
按照 大小排序,确定那个因素更重要
例子:应用场景
某地区国内生产总值的统计数据(以百万元计),问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大。
第一步:参考序列和对比序列确定
参考序列:GDP 对比序列:第一,二,三产业
第二步: 变量的无量纲化
选择均值化:
3:计算灰色关联系数
计算:
求最值:
max max = 0.031027
min min = 0.000105
取ρ = 0.5: 计算
4: 计算
= 0.508432 = 0.624296 =0.7573
可以看出该地区对GDP的影响:第三产业>第二产业>第一产业:
第二个实例:
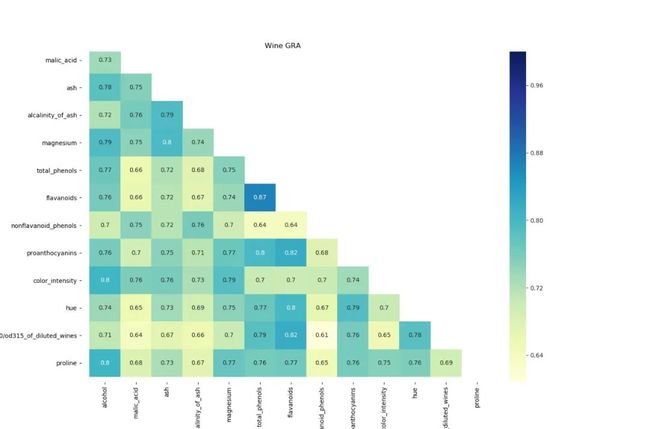
wine数据集:意大利同一地区生产的三种不同品种的酒,这些数据包括了三种酒中13种不同成分。分析13种成分之间联系?
# -*- coding: utf-8 -*-# @Time : 2020/9/9 16:16# @Author : wangboyang# @Site :# @File : WinGreForest_2020_9-9.py# @Software: PyCharm# @Function : # 灰色关联结果矩阵可视化import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.datasets import load_winewine = load_wine()data = wine.data #数据lables = wine.target #标签feaures = wine.feature_namesdf = pd.DataFrame(data,columns=feaures) #原始数据#第一步:无量纲化def standareData(df):"""df : 原始数据return : data 标准化的数据"""data =pd.DataFrame(index=df.index) #列名,一个新的dataframecolumns = df.columns.tolist() # 将列名提取出来for col in columns:d = df[col]max = d.max()min = d.min()mean = d.mean()data[col] = ((d-mean) /(max -min)).tolist()return data# 某一列当做参照序列,其他为对比序列def graOne(Data,m=0):"""return:"""columns = Data.columns.tolist() # 将列名提取出来#第一步:无量纲化data = standareData(Data)referenceSeq = data.iloc[:,m] #参考序列data.drop(columns[m],axis=1,inplace=True) # 删除参考列compareSeq = data.iloc[:,0:] #对比序列row,col = compareSeq.shape#第二步:参考序列 - 对比序列data_sub = np.zeros([row,col])for i in range(col):for j in range(row):data_sub[j,i] = abs(referenceSeq[j]-compareSeq.iloc[j,i])#找出最大值和最小值maxVal = np.max(data_sub)minVal = np.min(data_sub)cisi = np.zeros([row,col])for i in range(row):for j in range(col):cisi[i,j] = (minVal+0.5*maxVal) /(data_sub[i,j]+0.5*maxVal)#第三步:计算关联度result = [np.mean(cisi[:,i]) for i in range(col)]result.insert(m,1) #参照列为1return pd.DataFrame(result)def GRA(Data):df = Data.copy()columns = [str(s) for s in df.columns if s not in [None]] #[1 2 ,,,12]#print(columns)df_local = pd.DataFrame(columns=columns)df.columns =columnsfor i in range(len(df.columns)): #每一列都做参照序列,求关联系数df_local.iloc[:,i] = graOne(df,m=i)[0]df_local.index = columnsreturn df_local#热力图展示def ShowGRAHeatMap(DataFrame):colormap = plt.cm.hsvylabels = DataFrame.columns.values.tolist()f, ax = plt.subplots(figsize=(15, 15))ax.set_title('Wine GRA')# 设置展示一半,如果不需要注释掉mask即可mask = np.zeros_like(DataFrame)mask[np.triu_indices_from(mask)] = True # np.triu_indices 上三角矩阵with sns.axes_style("white"):sns.heatmap(DataFrame,cmap="YlGnBu",annot=True,mask=mask,)plt.show()data_wine_gra = GRA(df)ShowGRAHeatMap(data_wine_gra)
2:灰色预测
四种常见类型:
灰色时间序列预测
畸变预测
系统预测
拓扑预测
灰色生成数列:
为了挖掘数据中蕴含的内在规律,灰色系统通过对原始数据的整理来寻求其变化规律。即为灰色序列的生成,一切灰色序列都能某种生成弱化其随机性,显现其规律性。数据生成的常用方式有累加生成,累减生成,加权累加生成等。
灰色预测是以灰色模型为基础的,其中所建立的微分方程模型有很多种比如说GM(2,1),GM(1,1)等。
GM(1,1)
原始数据列:
n个数据个数
模型构建前检验:
当 时,可以GM(1,1)建模
数据预处理
原始数据累加以便弱化随机序列的波动性和随机性。
令:
得到新数据序列:
建立微分方:
其中a称为发展系数,b 灰色作用量,为待定系数
记:
,所以确定 a,b,就可以求出,从而求出
确定参数:
最小二乘法求解参数:
将灰参数带入 推出:
于是得到预测值:
从而相应得到预测值:
模型检验:
残差检验:计算相对残差
求级比:
级比偏差值检验:
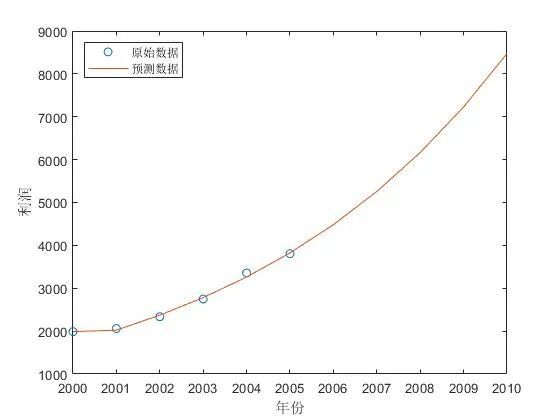
例子: 某地区国内生产总值的统计数据(以百万元计),问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大。 预测5年后GDP的变化趋势!
clear ;syms a b ;c = [a b]' ;%原始数据GDP = [1988 2061 2335 2750 3356 3806];X1 = cumsum(GDP) ;% 原始数据累加n = length(GDP) ;for i=1:(n-1)B_t(i) = (X1(i)+X1(i+1)) /2 ; %平均end%计算待定参数 a,bA = GDP ;A(1) = [] ;% 注意从2开始A = A' ; %列向量B=[-B_t ;ones(1,n-1)] ; %构造矩阵u = inv(B*B')*B*A ; %求解参数u = u' ;a = u(1) ;b = u(2) ;%根据a,b 预测5年以后GDP趋势F = [] ;F(1) = GDP(1) ;for i=2:(n+5)F(i) = (GDP(1)-b/a)/exp(a*(i-1)) + b/a ;endF0 = [] ;F0(1) = GDP(1) ;for i=2:(n+5)F0(i) =F(i) -F(i-1);endt1=2000:2005;t2=2000:2005+5;plot(t1,GDP,'o',t2,F0) %原始数据与预测数据的比较legend('原始数据','预测数据','Location','NorthWest');xlabel('年份')ylabel('利润')
Reference:
[1]:https://www.zhihu.com/searchtype=content&q=%E7%81%B0%E8%89%B2%E9%A2%84%E6%B5%8B
[2]: https://blog.csdn.net/FontThrone/article/details/80607794