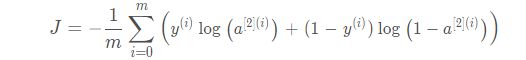吴恩达编程作业——搭建含一个隐藏层的神经网络进行数据分析
搭建含有一个隐藏层的神经网络
首先声明本文参考https://blog.csdn.net/u013733326/article/details/79702148,通过学习自己动手实现了前文中的所有功能,在此基础上实现了对于最后的“blobs”数据集的6分类,采用softmax进行多分类,希望交流学习
- testCases:提供了一些测试示例来评估函数的正确性,参见下载的资料或者在底部查看它的代码。
- planar_utils :提供了在这个任务中使用的各种有用的功能,参见下载的资料或者在底部查看它的代码。
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
%matplotlib inline #如果你使用用的是Jupyter Notebook的话请取消注释。
np.random.seed(1) #设置一个固定的随机种子,以保证接下来的步骤中我们的结果是一致的。
UsageError: unrecognized arguments: #如果你使用用的是Jupyter Notebook的话请取消注释。
加载和查看数据集
X, Y = load_planar_dataset()
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral) #绘制散点图
- X:一个numpy的矩阵,包含了这些数据点的数值
- Y: 一个numpy的向量,对应着的是X的标签(红色:0, 蓝色:1)
shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1]
print ("X的维度为: " + str(shape_X))
print ("Y的维度为: " + str(shape_Y))
print ("数据集里面的数据有:" + str(m) + " 个")
X的维度为: (2, 400)
Y的维度为: (1, 400)
数据集里面的数据有:400 个
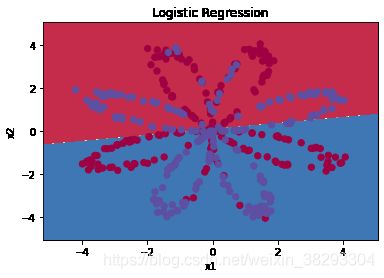
查看简单的Logistic回归的分类效果
我们可以使用sklearn的内置函数来查看逻辑回归在这个问题上表现
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)
F:\Program Files\Anaconda3\envs\tf2.0\lib\site-packages\sklearn\utils\validation.py:760: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
y = column_or_1d(y, warn=True)
LogisticRegressionCV(Cs=10, class_weight=None, cv=None, dual=False,
fit_intercept=True, intercept_scaling=1.0, l1_ratios=None,
max_iter=100, multi_class='auto', n_jobs=None,
penalty='l2', random_state=None, refit=True, scoring=None,
solver='lbfgs', tol=0.0001, verbose=0)
Y = np.squeeze(Y)
plot_decision_boundary(lambda x: clf.predict(x), X, Y) #绘制决策边界
plt.title("Logistic Regression") #图标题
LR_predictions = clf.predict(X.T) #预测结果
print ("逻辑回归的准确性: %d " % float((np.dot(Y, LR_predictions) +
np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) +
"% " + "(正确标记的数据点所占的百分比)")
逻辑回归的准确性: 47 % (正确标记的数据点所占的百分比)
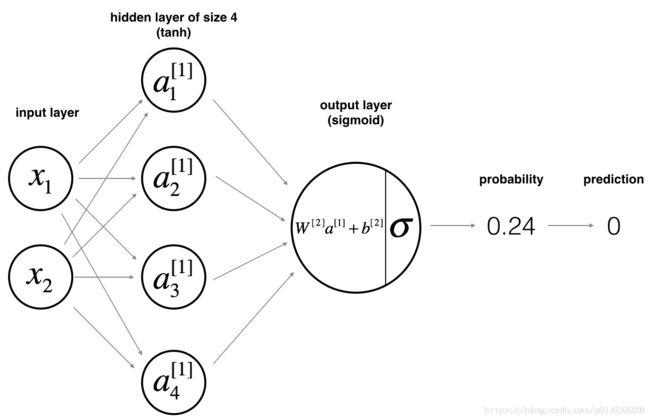
搭建神经网络
构建神经网络的一般方法是:
- 定义神经网络结构(输入单元的数量,隐藏单元的数量等)。
- 初始化模型的参数
- 循环:
- 实施前向传播
- 计算损失
- 实现向后传播
- 更新参数(梯度下降)
定义神经网络结构
def layer_sizes(X, Y):
"""
参数:
X - 输入数据集,维度为(输入的数量,训练/测试的数量)
Y - 标签,维度为(输出的数量,训练/测试数量)
返回:
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return (n_x, n_h, n_y)
#测试layer_sizes
print("=========================测试layer_sizes=========================")
X_asses , Y_asses = layer_sizes_test_case()
(n_x,n_h,n_y) = layer_sizes(X_asses,Y_asses)
print("输入层的节点数量为: n_x = " + str(n_x))
print("隐藏层的节点数量为: n_h = " + str(n_h))
print("输出层的节点数量为: n_y = " + str(n_y))
=========================测试layer_sizes=========================
输入层的节点数量为: n_x = 5
隐藏层的节点数量为: n_h = 4
输出层的节点数量为: n_y = 2
初始化模型的参数
np.random.randn(a,b)* 0.01来随机初始化一个维度为(a,b)的矩阵。np.zeros((a,b))用零初始化矩阵(a,b)。
def initialize_parameters(n_x, n_h, n_y):
"""
参数:
n_x - 输入层节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回:
parameters - 包含参数的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
np.random.seed(2) # 指定一个随机种子,以便你的输出与我们的一样
W1 = np.random.rand(n_h, n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.rand(n_y, n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
#使用断言确保我的数据格式是正确的
assert(W1.shape == ( n_h , n_x ))
assert(b1.shape == ( n_h , 1 ))
assert(W2.shape == ( n_y , n_h ))
assert(b2.shape == ( n_y , 1 ))
parameters = {
"W1" : W1,
"b1" : b1,
"W2" : W2,
"b2" : b2}
return parameters
#测试initialize_parameters
print("=========================测试initialize_parameters=========================")
n_x , n_h , n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x , n_h , n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试initialize_parameters=========================
W1 = [[0.00435995 0.00025926]
[0.00549662 0.00435322]
[0.00420368 0.00330335]
[0.00204649 0.00619271]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[0.00299655 0.00266827 0.00621134 0.00529142]]
b2 = [[0.]]
循环
前向传播
def forward_propagation(X , parameters):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 前向传播计算A2
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
# 使用断言确保数据的格式是正确的
assert(A2.shape == (1, X.shape[1]))
cache = {
"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return (A2, cache)
#测试forward_propagation
print("=========================测试forward_propagation=========================")
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
print(np.mean(cache["Z1"]), np.mean(cache["A1"]), np.mean(cache["Z2"]), np.mean(cache["A2"]))
=========================测试forward_propagation=========================
-0.0004997557777419902 -0.000496963353231779 0.00043818745095914653 0.500109546852431
计算损失
def compute_cost(A2, Y, parameters):
"""
计算方程(6)中给出的交叉熵成本,
参数:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为(1,数量)
parameters - 一个包含W1,B1,W2和B2的字典类型的变量
返回:
成本 - 交叉熵成本给出方程(13)
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
# 计算成本
logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1- A2), 1- Y)
cost = - np.sum(logprobs) / m
cost = float(np.squeeze(cost))
assert(isinstance(cost,float))
return cost
#测试compute_cost
print("=========================测试compute_cost=========================")
A2 , Y_assess , parameters = compute_cost_test_case()
print("cost = " + str(compute_cost(A2,Y_assess,parameters)))
=========================测试compute_cost=========================
cost = 0.6929198937761266
反向传播
def backward_propagation(parameters, cache, X , Y):
"""
使用上述说明搭建反向传播函数。
参数:
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型的变量。
X - 输入数据,维度为(2,数量)
Y - “True”标签,维度为(1,数量)
返回:
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {
"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads
#测试backward_propagation
print("=========================测试backward_propagation=========================")
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
=========================测试backward_propagation=========================
dW1 = [[ 0.01018708 -0.00708701]
[ 0.00873447 -0.0060768 ]
[-0.00530847 0.00369379]
[-0.02206365 0.01535126]]
db1 = [[-0.00069728]
[-0.00060606]
[ 0.000364 ]
[ 0.00151207]]
dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]]
db2 = [[0.06589489]]
更新权重
def update_parameters(parameters,grads,learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数:
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回:
parameters - 包含更新参数的字典类型的变量。
"""
W1,W2 = parameters["W1"],parameters["W2"]
b1,b2 = parameters["b1"],parameters["b2"]
dW1,dW2 = grads["dW1"],grads["dW2"]
db1,db2 = grads["db1"],grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
#测试update_parameters
print("=========================测试update_parameters=========================")
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试update_parameters=========================
W1 = [[-0.00643025 0.01936718]
[-0.02410458 0.03978052]
[-0.01653973 -0.02096177]
[ 0.01046864 -0.05990141]]
b1 = [[-1.02420756e-06]
[ 1.27373948e-05]
[ 8.32996807e-07]
[-3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]]
b2 = [[0.00010457]]
整合
def nn_model(X,Y,n_h,num_iterations,learning_rate=0.5,print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
np.random.seed(3) #指定随机种子
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(num_iterations):
A2 , cache = forward_propagation(X,parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters,grads,learning_rate = learning_rate)
if print_cost:
if i%1000 == 0:
print("第 ",i," 次循环,成本为:"+str(cost))
return parameters
#测试nn_model
print("=========================测试nn_model=========================")
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000,learning_rate=0.5, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
=========================测试nn_model=========================
F:\Program Files\Anaconda3\envs\tf2.0\lib\site-packages\ipykernel_launcher.py:18: RuntimeWarning: divide by zero encountered in log
E:\juypter notebook\吴恩达深度学习编程作业\新建文件夹\planar_utils.py:25: RuntimeWarning: overflow encountered in exp
s = 1/(1+np.exp(-x))
W1 = [[ 6.77962262 -1.20251908]
[ 3.88054479 -4.78255014]
[ 6.77957337 -1.20259341]
[ 3.91283855 -4.76226051]]
b1 = [[-3.41156836]
[-2.11502992]
[-3.41180795]
[-2.11394815]]
W2 = [[2501.9026286 2512.05642635 2502.1219803 2511.85584867]]
b2 = [[-22.61274856]]
预测
def predict(parameters,X):
"""
使用学习的参数,为X中的每个示例预测一个类
参数:
parameters - 包含参数的字典类型的变量。
X - 输入数据(n_x,m)
返回
predictions - 我们模型预测的向量(红色:0 /蓝色:1)
"""
A2 , cache = forward_propagation(X,parameters)
predictions = np.round(A2)
return predictions
#测试predict
print("=========================测试predict=========================")
parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("预测的平均值 = " + str(np.mean(predictions)))
=========================测试predict=========================
预测的平均值 = 0.6666666666666666
X, Y = load_planar_dataset()
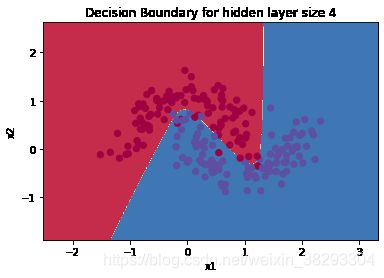
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000,learning_rate=0.5, print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, np.squeeze(Y))
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
第 0 次循环,成本为:0.6931586620054873
第 1000 次循环,成本为:0.3105418538607143
第 2000 次循环,成本为:0.2933016516189315
第 3000 次循环,成本为:0.284426182780695
第 4000 次循环,成本为:0.27809983960632034
第 5000 次循环,成本为:0.2729885982112937
第 6000 次循环,成本为:0.2658930763526426
第 7000 次循环,成本为:0.24033551091862504
第 8000 次循环,成本为:0.2339493804055549
第 9000 次循环,成本为:0.23001665584776734
准确率: 90%
更改隐藏层节点数量
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 50] #隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i + 1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations=5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, np.squeeze(Y))
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("隐藏层的节点数量: {} ,准确率: {} %".format(n_h, accuracy))
隐藏层的节点数量: 1 ,准确率: 67.25 %
隐藏层的节点数量: 2 ,准确率: 66.5 %
隐藏层的节点数量: 3 ,准确率: 89.5 %
隐藏层的节点数量: 4 ,准确率: 89.75 %
隐藏层的节点数量: 5 ,准确率: 90.25 %
隐藏层的节点数量: 10 ,准确率: 90.75 %
隐藏层的节点数量: 50 ,准确率: 90.0 %
探索
# 数据集
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {
"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
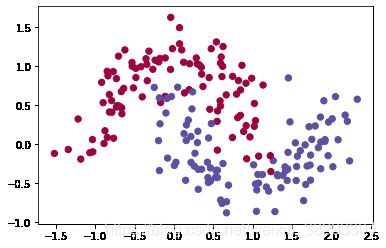
dataset = "noisy_moons"
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000,learning_rate= 0.5 ,print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, np.squeeze(Y))
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
第 0 次循环,成本为:0.6931438511638413
第 1000 次循环,成本为:0.32654432451789817
第 2000 次循环,成本为:0.32589266506729897
第 3000 次循环,成本为:0.32556680216270645
第 4000 次循环,成本为:0.32528794843480896
第 5000 次循环,成本为:0.32471534759736703
第 6000 次循环,成本为:0.11358931682256697
第 7000 次循环,成本为:0.09821826543340158
第 8000 次循环,成本为:0.09515334310454593
第 9000 次循环,成本为:0.09372601272443966
准确率: 96%
X, Y = datasets["noisy_circles"]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KQ01ye8y-1595750917075)(output_47_1.png)]
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000,learning_rate= 0.5 ,print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, np.squeeze(Y))
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
第 0 次循环,成本为:0.6931457786347083
第 1000 次循环,成本为:0.6883960605426281
第 2000 次循环,成本为:0.4414841278453237
第 3000 次循环,成本为:0.4340232169269984
第 4000 次循环,成本为:0.432230474912991
第 5000 次循环,成本为:0.43091913604989246
第 6000 次循环,成本为:0.4283296739374367
第 7000 次循环,成本为:0.41972866670866454
第 8000 次循环,成本为:0.4137252336321846
第 9000 次循环,成本为:0.4119040213719174
准确率: 80%
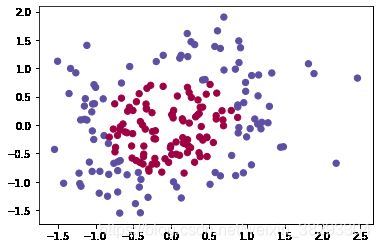
X, Y = datasets["gaussian_quantiles"]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000,learning_rate= 0.5 ,print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, np.squeeze(Y))
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
第 0 次循环,成本为:0.6931432224936229
第 1000 次循环,成本为:0.23416382246698736
第 2000 次循环,成本为:0.10421006990099499
第 3000 次循环,成本为:0.0826544174858772
第 4000 次循环,成本为:0.07163531039648277
第 5000 次循环,成本为:0.06465496567803554
第 6000 次循环,成本为:0.0597297842318288
第 7000 次循环,成本为:0.05601638389122446
第 8000 次循环,成本为:0.05308711695055919
第 9000 次循环,成本为:0.05069906108856062
准确率: 99%
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Hv5tyqOD-1595750917078)(output_50_1.png)]
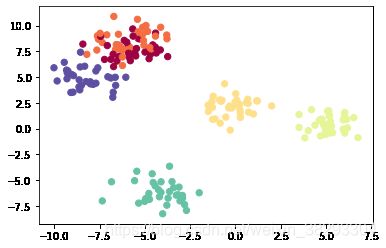
X, Y = datasets["blobs"]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
实现对blobs数据的分类
Y
array([[2, 3, 4, 3, 1, 2, 5, 2, 0, 2, 0, 1, 0, 0, 4, 2, 0, 4, 4, 2, 4, 1,
2, 5, 1, 0, 5, 0, 2, 3, 4, 2, 3, 0, 5, 2, 2, 0, 2, 5, 0, 4, 1, 1,
0, 0, 3, 5, 0, 0, 2, 0, 3, 0, 5, 2, 5, 2, 1, 0, 2, 4, 4, 2, 5, 4,
3, 5, 1, 4, 2, 3, 2, 1, 1, 4, 1, 3, 1, 3, 2, 3, 4, 5, 1, 4, 4, 0,
0, 2, 4, 2, 5, 4, 0, 4, 5, 3, 1, 3, 3, 1, 0, 1, 2, 1, 1, 3, 3, 0,
5, 0, 5, 2, 1, 5, 3, 3, 1, 4, 2, 5, 1, 3, 3, 5, 2, 1, 3, 4, 0, 5,
1, 1, 1, 5, 3, 1, 0, 0, 5, 3, 5, 5, 2, 3, 5, 4, 1, 0, 5, 4, 2, 5,
5, 2, 0, 0, 1, 3, 3, 3, 3, 0, 2, 4, 0, 4, 4, 1, 3, 0, 4, 5, 2, 4,
4, 5, 1, 1, 3, 5, 1, 4, 4, 1, 2, 5, 0, 4, 3, 1, 5, 4, 3, 4, 2, 5,
3, 0]])
X.shape, Y.shape
((2, 200), (1, 200))
# 定义处理blobs数据的模型结构
n_x = X.shape[0]
n_h = 4
n_y = Y.max() + 1
n_x, n_h, n_y
(2, 4, 6)
# 初始化参数权重
np.random.seed(2) #指定一个随机种子,以便你的输出与我们的一样。
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
# 将Y转换为 one-hot矩阵
num_class = 6
Y_onehot = np.eye(num_class)[Y]
Y_onehot = np.squeeze(Y_onehot)
Y_onehot, Y_onehot.shape
(array([[0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 1., 0.],
...,
[0., 0., 0., 0., 0., 1.],
[0., 0., 0., 1., 0., 0.],
[1., 0., 0., 0., 0., 0.]]), (200, 6))
# 实现softmax函数
def sotfmax(Z):
A = np.exp(Z)/np.sum(np.exp(Z))
return A
# 前向传播
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sotfmax(Z2)
A2.shape
(6, 200)
# 定义损失函数
Y_onehot = Y_onehot.transpose(1,0)
logprobs = np.multiply(Y_onehot, np.log(A2))
cost = - np.sum(logprobs) / 200
cost = float(np.squeeze(cost))
cost
7.091483556059716
# 反向传播
dZ2= A2 - Y_onehot
dW2 = (1 / 200) * np.dot(dZ2, A1.T)
db2 = (1 / 200) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / 200) * np.dot(dZ1, X.T)
db1 = (1 / 200) * np.sum(dZ1, axis=1, keepdims=True)
# 更新权重
learning_rate =0.5
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
## 整合
X, Y = datasets["blobs"]
X, Y = X.T, Y.reshape(1, Y.shape[0])
if dataset == "blobs":
Y = Y % 2
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
num_class = 6
num_x = 200
num_iterations = 100000
learning_rate =0.001
# 定义处理blobs数据的模型结构
n_x = X.shape[0]
n_h = 10
n_y = 6
# 将Y转换为 one-hot矩阵
Y_onehot = np.eye(num_class)[Y]
Y_onehot = np.squeeze(Y_onehot)
Y_onehot = Y_onehot.transpose(1,0)
# 实现softmax函数
def sotfmax(Z):
A = np.exp(Z)/np.sum(np.exp(Z),axis=0)
return A
# 初始化参数权重
np.random.seed(3) #指定一个随机种子,以便你的输出与我们的一样。
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
for i in range(num_iterations):
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sotfmax(Z2)
logprobs = np.multiply(Y_onehot, np.log(A2))
cost = - np.sum(logprobs) / num_x
cost = float(np.squeeze(cost))
dZ2= A2 - Y_onehot
dW2 = (1 / num_x) * np.dot(dZ2, A1.T)
db2 = (1 / num_x) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / num_x) * np.dot(dZ1, X.T)
db1 = (1 / num_x) * np.sum(dZ1, axis=1, keepdims=True)
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
if i%1000 == 0:
print("第 ",i," 次循环,成本为:"+str(cost))
第 0 次循环,成本为:1.7916803120519142
第 1000 次循环,成本为:1.7287543276996202
第 2000 次循环,成本为:1.4461862433784824
第 3000 次循环,成本为:1.2130951767271876
第 4000 次循环,成本为:1.0504657310659369
第 5000 次循环,成本为:0.9289667117694779
第 6000 次循环,成本为:0.8339634075805266
第 7000 次循环,成本为:0.7582116939107046
第 8000 次循环,成本为:0.6969300121174165
第 9000 次循环,成本为:0.6463576785880705
第 10000 次循环,成本为:0.6037214465939013
第 11000 次循环,成本为:0.5671373029556971
第 12000 次循环,成本为:0.5353717776708582
第 13000 次循环,成本为:0.5076026659046426
第 14000 次循环,成本为:0.4832457378627725
第 15000 次循环,成本为:0.46184529638437655
第 16000 次循环,成本为:0.44301376011003696
第 17000 次循环,成本为:0.4264078430887138
第 18000 次循环,成本为:0.4117247951871863
第 19000 次循环,成本为:0.39870275045015147
第 20000 次循环,成本为:0.3871183687659884
第 21000 次循环,成本为:0.3767821280709222
第 22000 次循环,成本为:0.36753307885348235
第 23000 次循环,成本为:0.35923405828954086
第 24000 次循环,成本为:0.3517676516558599
第 25000 次循环,成本为:0.3450328907510301
第 26000 次循环,成本为:0.3389425873602622
第 27000 次循环,成本为:0.33342118277816757
第 28000 次循环,成本为:0.3284030037338915
第 29000 次循环,成本为:0.3238308334955287
第 30000 次循环,成本为:0.3196547268521986
第 31000 次循环,成本为:0.31583101542866393
第 32000 次循环,成本为:0.31232146399039123
第 33000 次循环,成本为:0.30909254897206273
第 34000 次循环,成本为:0.306114837963486
第 35000 次循环,成本为:0.3033624540524739
第 36000 次循环,成本为:0.3008126124436669
第 37000 次循环,成本为:0.2984452191924288
第 38000 次循环,成本为:0.2962425236066932
第 39000 次循环,成本为:0.2941888171392911
第 40000 次循环,成本为:0.29227017258416377
第 41000 次循环,成本为:0.2904742182012941
第 42000 次循环,成本为:0.28878994208447795
第 43000 次循环,成本为:0.28720752268546235
第 44000 次循环,成本为:0.2857181819355407
第 45000 次循环,成本为:0.2843140578719986
第 46000 次循环,成本为:0.282988094088693
第 47000 次循环,成本为:0.2817339436927442
第 48000 次循环,成本为:0.28054588576732736
第 49000 次循环,成本为:0.27941875261814486
第 50000 次循环,成本为:0.27834786632243086
第 51000 次循环,成本为:0.2773289833082769
第 52000 次循环,成本为:0.27635824587241115
第 53000 次循环,成本为:0.2754321396998421
第 54000 次循环,成本为:0.27454745658220275
第 55000 次循环,成本为:0.27370126164610803
第 56000 次循环,成本为:0.2728908645009587
第 57000 次循环,成本为:0.2721137937996528
第 58000 次循环,成本为:0.2713677747775942
第 59000 次循环,成本为:0.2706507093969077
第 60000 次循环,成本为:0.269960658775352
第 61000 次循环,成本为:0.26929582762428944
第 62000 次循环,成本为:0.2686545504582729
第 63000 次循环,成本为:0.26803527937122135
第 64000 次循环,成本为:0.2674365732015069
第 65000 次循环,成本为:0.2668570879312083
第 66000 次循环,成本为:0.2662955681838478
第 67000 次循环,成本为:0.26575083970062346
第 68000 次循环,成本为:0.26522180268796774
第 69000 次循环,成本为:0.26470742593968144
第 70000 次循环,成本为:0.264206741645413
第 71000 次循环,成本为:0.2637188408043773
第 72000 次循环,成本为:0.2632428691694299
第 73000 次循环,成本为:0.26277802365241615
第 74000 次循环,成本为:0.262323549127462
第 75000 次循环,成本为:0.26187873557486563
第 76000 次循环,成本为:0.2614429155145829
第 77000 次循环,成本为:0.2610154616849604
第 78000 次循环,成本为:0.2605957849291499
第 79000 次循环,成本为:0.2601833322582616
第 80000 次循环,成本为:0.2597775850664343
第 81000 次循环,成本为:0.25937805747831477
第 82000 次循环,成本为:0.2589842948137168
第 83000 次循环,成本为:0.2585958721573664
第 84000 次循环,成本为:0.25821239302365007
第 85000 次循环,成本为:0.2578334881073088
第 86000 次循环,成本为:0.2574588141112612
第 87000 次循环,成本为:0.2570880526424556
第 88000 次循环,成本为:0.2567209091660916
第 89000 次循环,成本为:0.25635711200795486
第 90000 次循环,成本为:0.2559964113941652
第 91000 次循环,成本为:0.255638578517493
第 92000 次循环,成本为:0.2552834046196587
第 93000 次循环,成本为:0.254930700079723
第 94000 次循环,成本为:0.2545802934998229
第 95000 次循环,成本为:0.25423203078106177
第 96000 次循环,成本为:0.2538857741842426
第 97000 次循环,成本为:0.2535414013722579
第 98000 次循环,成本为:0.2531988044331816
第 99000 次循环,成本为:0.2528578888853391
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
# np.meshgrid()将一维生成二维
xx, yy = np.meshgrid(np.arange(x_min, x_max, .02),
np.arange(y_min, y_max, .02))
# np.c_[]将数据合并合成两列 ravel()将数据降为一维
Z1 = np.dot(W1, (np.c_[xx.ravel(), yy.ravel()]).T) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sotfmax(Z2)
A2 = np.argmax(A2, axis=0)
A2 = A2.reshape(xx.shape)
# cmap设置样式 pcolormesh绘制分类图
# plt.pcolormesh(xx, yy, A2, cmap=plt.cm.Spectral, alpha=0.8)
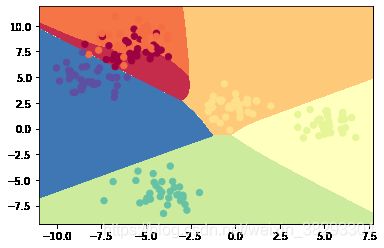
plt.contourf(xx, yy, A2, cmap=plt.cm.Spectral)
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral)
plt.show()
planar_utils文件内容
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
def plot_decision_boundary(model, X, Y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral) #绘制散点图
def sigmoid(x):
s = 1/(1+np.exp(-x))
return s
def load_planar_dataset():
np.random.seed(1)
m = 400 # number of examples
N = int(m/2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m,D)) # data matrix where each row is a single example
Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2):
ix = range(N*j,N*(j+1))
t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
def load_extra_datasets():
N = 200
noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
no_structure = np.random.rand(N, 2), np.random.rand(N, 2)
return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure
testCases
#-*- coding: UTF-8 -*-
"""
# WANGZHE12
"""
import numpy as np
def layer_sizes_test_case():
np.random.seed(1)
X_assess = np.random.randn(5, 3)
Y_assess = np.random.randn(2, 3)
return X_assess, Y_assess
def initialize_parameters_test_case():
n_x, n_h, n_y = 2, 4, 1
return n_x, n_h, n_y
def forward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {
'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
return X_assess, parameters
def compute_cost_test_case():
np.random.seed(1)
Y_assess = np.random.randn(1, 3)
parameters = {
'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
a2 = (np.array([[ 0.5002307 , 0.49985831, 0.50023963]]))
return a2, Y_assess, parameters
def backward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
parameters = {
'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
cache = {
'A1': np.array([[-0.00616578, 0.0020626 , 0.00349619],
[-0.05225116, 0.02725659, -0.02646251],
[-0.02009721, 0.0036869 , 0.02883756],
[ 0.02152675, -0.01385234, 0.02599885]]),
'A2': np.array([[ 0.5002307 , 0.49985831, 0.50023963]]),
'Z1': np.array([[-0.00616586, 0.0020626 , 0.0034962 ],
[-0.05229879, 0.02726335, -0.02646869],
[-0.02009991, 0.00368692, 0.02884556],
[ 0.02153007, -0.01385322, 0.02600471]]),
'Z2': np.array([[ 0.00092281, -0.00056678, 0.00095853]])}
return parameters, cache, X_assess, Y_assess
def update_parameters_test_case():
parameters = {
'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
grads = {
'dW1': np.array([[ 0.00023322, -0.00205423],
[ 0.00082222, -0.00700776],
[-0.00031831, 0.0028636 ],
[-0.00092857, 0.00809933]]),
'dW2': np.array([[ -1.75740039e-05, 3.70231337e-03, -1.25683095e-03,
-2.55715317e-03]]),
'db1': np.array([[ 1.05570087e-07],
[ -3.81814487e-06],
[ -1.90155145e-07],
[ 5.46467802e-07]]),
'db2': np.array([[ -1.08923140e-05]])}
return parameters, grads
def nn_model_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
return X_assess, Y_assess
def predict_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {
'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
return parameters, X_assess
参考
https://blog.csdn.net/u013733326/article/details/79702148