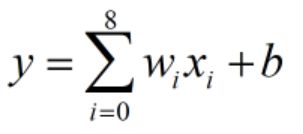台大机器学习李宏毅作业一（PM2.5预测）

机器学习李宏毅作业一（PM2.5预测）

1. 本文较大篇幅引用了博主秋沐霖的一篇博客https://www.cnblogs.com/HL-space/p/10676637.html，源博主思路很清晰，很好地帮助我学习这部分知识。
2. 刚开始学习机器学习和python编程，许多地方似懂非懂，在源博主的代码基础上进行了更改，难免内容繁杂，格式不规范，也望大神指教。
3. 本文实现了博主秋沐霖的改进思路，在同样训练2000次后，将训练集上的loss data从43.613降到了39.169，将测试集上的loss data从40.354降到了34.933。

一、基本原理

​ 题目是根据前九小时的PM2.5值来预测第十小时的值，是一种典型的回归问题(回归问题多用来预测一个具体的数值)。

回归问题是机器学习三大基本模型中很重要的一环，其功能是建模和分析变量之间的关系.

面对一个回归问题，我们可简要描述其求解流程：

1. 选定训练模型，即我们为程序选定一个求解框架，如线性回归模型(Linear Regression)等。

2. 导入训练集 train_set，即给模型提供大量可供学习参考的正确数据。

3. 选择合适的学习算法，通过训练集中大量输入输出结果让程序不断优化输入数据与输出数据间的关联性，从而提升模型的预测准确度。

4. 在训练结束后即可让模型预测结果，我们为程序提供一组新的输入数据，模型根据训练集的学习成果来预测这组输入对应的输出值。

   ​ ------摘自知乎YangYH408

​ 下面从模型入手开始解决问题:

1.1、模型建立

采用最普通的线性回归模型，并没有用上训练集中所有的数据，只用到了每个数据帧样本中的9个PM2.5含量值：

为对应数据帧中第i个PM2.5含量，为其对应的权重值，为偏置项，为该数据帧样本的预测结果。

1.2、损失函数

​ 损失函数定义了拟合结果和真实结果之间的差异，作为优化的目标直接关系模型训练的好坏。

​ 常用损失函数小结

​ 最小二乘法介绍

​ 这里采用均方差损失函数(常用在最小二乘法中)，式中除以2的目的是便于求导计算:
​
为第n个label，为第n个数据帧的预测结果，为参加训练的数据帧样本个数。
　　为了防止过拟合，加入正则项：
　　
​
为正则项，为正则项系数。
加入正则项可以限制模型复杂度，防止过拟合出现。这一块感觉似懂非懂，希望后续学习能完善。

1.3、梯度下降法

​ 梯度下降法讲解

梯度计算：需明确此时的目标是使Loss最小，而可优化的参数为权重w和偏置值b，因此需要求Loss在w上的偏微分和Loss在b上的偏微分，求权重梯度时，源博客结果多了个求和符号？

　　计算出梯度后，通过梯度下降法实现参数更新。

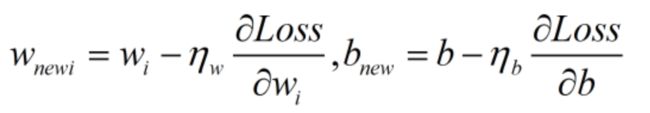
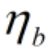为权重w更新时的学习率，为偏置b更新时的学习率。

1.4、学习率更新

为了在不影响模型效果的前提下提高学习速度，可以对学习率进行实时更新：即让学习率的值在学习初期较大，之后逐渐减小。这里采用比较经典的adagrad算法来更新学习率。

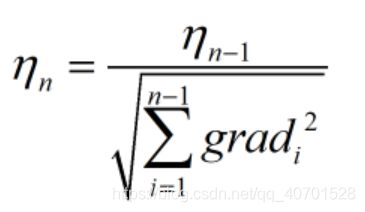
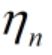为更新后的学习率，为更新前的学习率。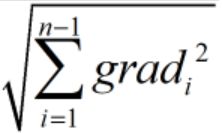为在此之前所有梯度平方和的二次根。

​ 学习率不能太大也不能太小，学习率过小收敛过程如下：

​ 学习率过大时收敛过程如下：

​ 可见，学习率过小，收敛过程十分缓慢；学习率过大会出现来回震荡，甚至不收敛。最好的情况便是刚开始学习率较大，随着训练的进行逐渐减小，这样结果会在最优值出小幅摆动。刚开始训练时学习率一般取0.01 ~ 0.001 ，可尝试更改。具体怎样找出最佳的学习率？希望后续学习能让我搞明白。。。

二、代码实现

2.1、导入库

import pandas as pd
import numpy as np
from matplotlib import pylab as pyl 

库介绍：

pandas库简介

numpy库简介

2.2、读入数据集

数据集下载：https://pan.baidu.com/s/1o2Yx42dZBJZFZqCa5y3WzQ，提取码：qgtm。

data = pd.read_csv('E:\\机器学习李宏毅\\作业\\PM2.5预测\\train.csv')
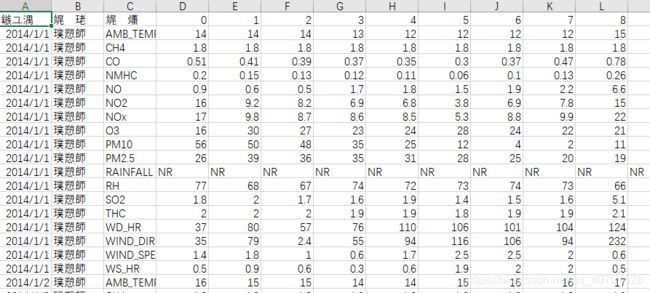
data = data.iloc[:, 3:]                       #将所有行和从第三列开始的所有列保留即留下有效数据
data = data.replace(['NR'], [0.0])            #将NR用0替换

括号里替换为文件路径，不知为啥用’\'不行得用‘\\’;

pd.read_csv()用法：https://blog.csdn.net/weixin_42462804/article/details/100132767

pandas-dataframe 介绍及基础操作:https://www.jianshu.ctom/p/8024ceef4fe2

源数据集如下：

可见需要把前三列除掉，将书据中的NR用0代替。

2.3、处理数据集

def DateProcess(df):
    x_list, y_list = [], []                   #初始化两个列表
    array = np.array(df).astype(float)        #将dataframe类型转换成数组
    x=array[0:18,:]                           #将第一天的数据提取到x
    for i in range(18,4320,18):               
        mat=array[i:i+18,:]                   #将每一天的数据提取出来
        x = np.hstack((x,mat))                #进行行组合       
    for i in range(0,5760-9):                 #提取出PM2.5的值
        label=x[9,i+9]
        y_list.append(label)
    for i in range(0,5760-9):
        mat=x[:,i:i+9]
        x_list.append(mat)
    y = np.array(y_list)                   #转换成数组类型
    x = np.array(x_list)                   #转换成数组类型
    return x, y

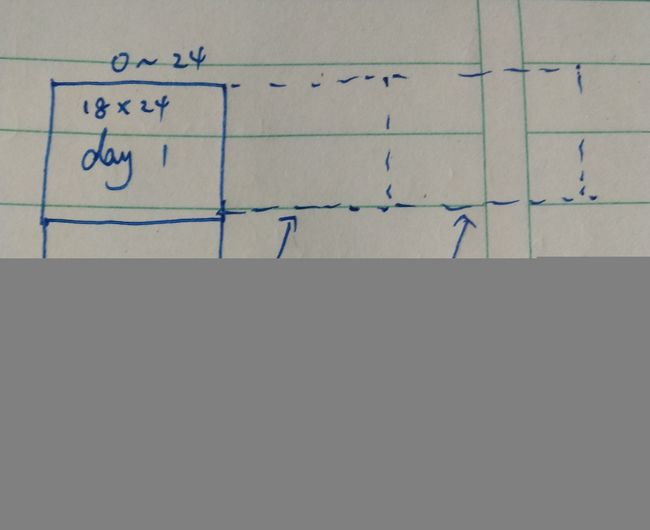
引用的博主采用划分数据集的方法见博文，但这样做的话，一天中前九个小时的PM2.5值并没有利用上，如该博主所说，时间是连续的，没有必要按天分割开。按照这一思路，将每一天的数据都连接起来如下图：

如此划分后将原来的3600组训练数据扩增到了5751组，能使模型精度得到优化。

2.4、模型训练

# 更新参数，训练模型
def train(x_train, y_train, epoch):
    bias = 0                                 # 偏置值初始化
    weights = np.ones(9)                     # 初始化权重为九个一
    learning_rate = 1                        # 初始学习率
    reg_rate = 0.001                         # 正则项系数
    bg2_sum = 0                              # 用于存放偏置值的梯度平方和
    wg2_sum = np.zeros(9)                    # 用于存放权重的梯度平方和

    for i in range(epoch):                  #训练epoch次
        b_g = 0          
        w_g = np.zeros(9)                    #计算梯度
        for j in range(5000):
            b_g += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-1)
            for k in range(9):
                w_g[k] += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-x_train[j, 9, k])    
        b_g /= 5000
        w_g /= 5000
        #  加上Loss_regularization在w上的梯度
        for m in range(9):
            w_g[m] += reg_rate * weights[m]
        
        # adagrad
        bg2_sum += b_g**2
        wg2_sum += w_g**2
        # 更新权重和偏置
        bias -= learning_rate/bg2_sum**0.5 * b_g
        weights -= learning_rate/wg2_sum**0.5 * w_g
        
        if i%4==0:
            loss = 0
            for j in range(5000):
                loss += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias)**2
            print('after {} epochs, the loss on train data is:'.format(i), loss/5000)

    return weights, bias

y_train为PM2.5值，x_train为处理完的数据集分出开的验证集，epoch为训练轮数。

2.5、模型测试

def validate(x_val, y_val, weights, bias):
    loss = 0
    a=np.zeros(751)
    for i in range(751):
        loss += (y_val[i] - weights.dot(x_val[i, 9, :]) - bias)**2
        a[i]=weights.dot(x_val[i, 9, :])
    return loss / 751,a

np.zeros()创建为零的数组。

x_var和y_var为验证集的数据集和PM2.5值；weights和bias为训练好的权重和偏置。

2.6、完整源程序

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def DateProcess(df):
    x_list, y_list = [], []                   #初始化两个列表
    array = np.array(df).astype(float)        #将dataframe类型转换成数组
    x=array[0:18,:]                           #将第一天的数据提取到x
    for i in range(18,4320,18):              
        mat=array[i:i+18,:]
        x = np.hstack((x,mat))
    for i in range(0,5760-9):
        label=x[9,i+9]
        y_list.append(label)
    for i in range(0,5760-9):
        mat=x[:,i:i+9]
        x_list.append(mat)
    y = np.array(y_list)                   #转换成数组类型
    x = np.array(x_list)                   #转换成数组类型
    return x, y

# 更新参数，训练模型
def train(x_train, y_train, epoch):
    bias = 0                                 # 偏置值初始化
    weights = np.ones(9)                     # 初始化权重为九个一
    learning_rate = 1                        # 初始学习率
    reg_rate = 0.001                         # 正则项系数
    bg2_sum = 0                              # 用于存放偏置值的梯度平方和
    wg2_sum = np.zeros(9)                    # 用于存放权重的梯度平方和

    for i in range(epoch):                  #训练epoch次
        b_g = 0          
        w_g = np.zeros(9)                    #计算梯度
        for j in range(5000):
            b_g += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-1)
            for k in range(9):
                w_g[k] += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-x_train[j, 9, k])    
        b_g /= 5000
        w_g /= 5000
        #  加上Loss_regularization在w上的梯度
        for m in range(9):
            w_g[m] += reg_rate * weights[m]
        
        # adagrad
        bg2_sum += b_g**2
        wg2_sum += w_g**2
        # 更新权重和偏置
        bias -= learning_rate/bg2_sum**0.5 * b_g
        weights -= learning_rate/wg2_sum**0.5 * w_g
        
        if i%4==0:
            loss = 0
            for j in range(5000):
                loss += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias)**2
            print('after {} epochs, the loss on train data is:'.format(i), loss/5000)

    return weights, bias

def validate(x_val, y_val, weights, bias):
    loss = 0
    a=np.zeros(751)
    for i in range(751):
        loss += (y_val[i] - weights.dot(x_val[i, 9, :]) - bias)**2
        a[i]=weights.dot(x_val[i, 9, :])
    return loss / 751,a

def main():
     # 从csv中读入数据
    data = pd.read_csv('E:\\机器学习李宏毅\\作业\\PM2.5预测\\train.csv')
    data = data.iloc[:, 3:]                       #将所有行和从第三列开始的所有列保留即留下有效数据
    data = data.replace(['NR'], [0.0])            #将NR用0替换
    x, y = DateProcess(data)
    x_train, y_train = x[0:5000], y[0:5000]
    x_val, y_val = x[5000:5751], y[5000:5751]
    epoch = 2000 # 训练轮数
    # 开始训练
    w, b = train(x_train, y_train, epoch)
    # 在验证集上看效果
    loss,c = validate(x_val, y_val, w, b)
    print('The loss on val data is:', loss)
    x=range(0,751)
    x=list(x)
    plt.plot(x,y_val,'ob')
    plt.plot(x,c,'or')
    plt.show()  
    if __name__ == '__main__':
        main()

在源程序中我将训练集和测试集按5000和751划分，怎样划分最好也还有待学习。

三、输出结果

每训练四轮输出一次训练集上的loss data。（辣鸡电脑，隔太久我会怀疑它卡了）

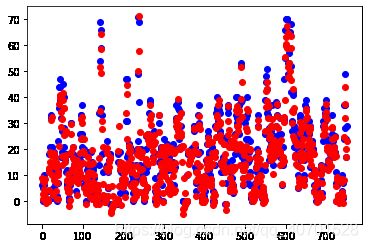
最终结果：

图中，蓝色为真实值，红色为预测值；可以看出增加数据集后模型精度确实上升了。