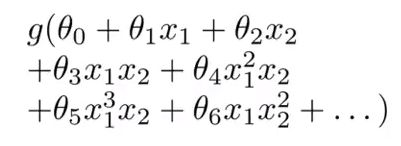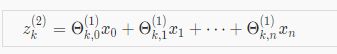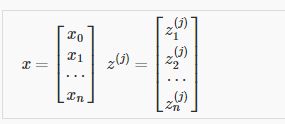本文将会介绍一种叫“神经网络”(Neural Network)的机器学习算法。
非线性假设
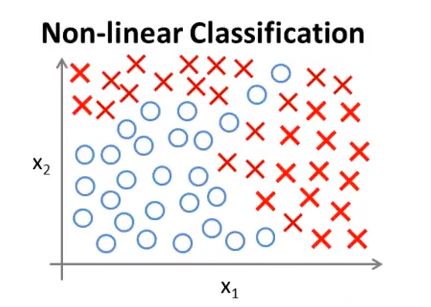
我们之前已经学习过线性回归和逻辑回归算法了,为什么还要研究神经网络? 我们先看一个例子。下面是一个监督学习分类问题的训练集:
如果利用逻辑回归算法来解决这个问题,首先需要构造一个包含很多非线性项的逻辑回归函数。如下所示:
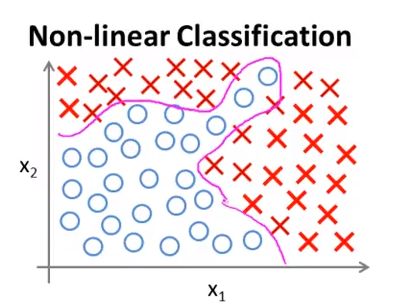
这里g仍是sigmod函数,我们能让函数,包含很多像这样的多项式项。事实上,当多项式项数足够多时,那么可能你能够得到一个分开正负样本的曲线:
这里只有$x_1$和$x_2$两项,因此可以得出不错的结果。但如果应对一些复杂的机器学习问题时,设计的项往往多余两项。假设我们要预测某房子未来半年卖出去的可能性,这是一个分类问题,而特征项可能有比如面积,层数,房间数等等很多,那么我们构建出来的函数将会很复杂,其中二次项的数目可能达到$\frac{n^2}{2}$,而且由于项数过多,可能会导致过拟合问题。除此之外,运算量显然也是很庞大的。不过也可以试试只加入这些二次项的子集,比如$x_1^2$,$x_2^2$,$x_n^2$,这样就只有n个二次项,但由于忽略了太多二次项,得到的结果可能会不准确。再者,这里只讨论了二次项,那三次项的数量同样也是很多的。所以,当初始特征个数n增大时 这些高阶多项式项数将以几何级数递增,特征空间也随之急剧膨胀,当特征个数n很大时找出附加项来建立一些分类器,这显然并不是一个好做法。
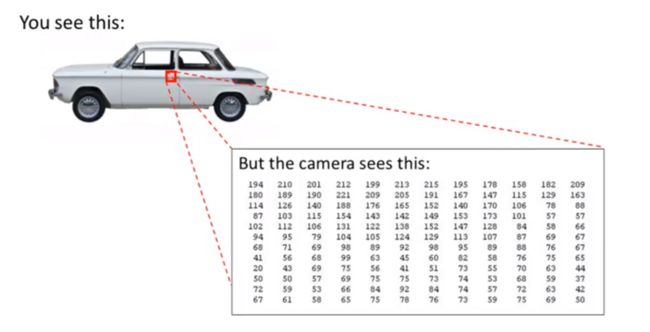
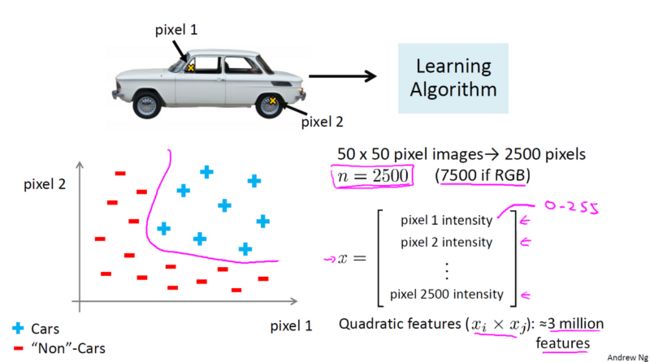
对于实际的很多机器学习问题,特征个数n是很大的。比如一个计算机视觉的问题,假设你想要使用机器学习算法来训练一个分类器,使它检测一个图像,来判断图像是否为一辆汽车。我们取出这幅图片中的一小部分将其放大,比如图中这个红色方框内的部分,结果表明,当人眼看到一辆汽车时,计算机实际上看到的却是这个一个数据矩阵或像这种格网,它们表示了像素强度值,告诉我们图像中每个像素的亮度值。因此对于计算机视觉来说问题就变成了,根据这个像素点亮度矩阵来告诉我们这些数值代表一个汽车门把手。
具体而言,当用机器学习算法构造一个汽车识别器时,我们要想出一个带标签的样本集,其中一些样本是各类汽车,另一部分样本是其他任何东西,将这个样本集输入给学习算法,以训练出一个分类器,训练完毕后,我们输入一幅新的图片,让分类器判定,“这是什么东西?”。为了理解引入非线性分类器的必要性,我们从学习算法的训练样本中挑出一些汽车图片和一些非汽车图片。
让我们从其中每幅图片中挑出一组像素点,像素点1和像素点2,在坐标系中标出这幅汽车的位置,在某一点上车的位置取决于像素点1和像素点2的亮度。让我们用同样的方法标出其他图片中汽车的位置,然后我们再举几个 关于汽车的不同的例子,观察这两个相同的像素位置。我们用“+”代表是汽车,“-”代表非汽车,这些数据分布在坐标系的不同位置,我们需要一个非线性分类器来分开这两类样本。假设我们用50*50像素的图片,那么久一共是2500个像素点。因此,我们的特征向量的元素数量N=2500,特征向量X包含了所有像素点的亮度值,对于典型的计算机图片表示方法,如果存储的是每个像素点的灰度值,(色彩的强烈程度),那么每个元素的值,应该在0到255之间,因此,这个问题中n=2500,但是,这只是使用灰度图片的情况,如果我们用的是RGB彩色图像,每个像素点包含红、绿、蓝三个子像素,那么n=7500。
因此,如果我们非要通过包含所有的二次项来解决这个非线性问题,那么,这就是式子中的所有条件,$x_i*x_j$,连同开始的2500像素,总共大约有300万个,这数字大得有点离谱了,对于每个样本来说,要发现并表示,所有这300万个项,这计算成本太高了。因此,只是简单的增加二次项或者三次项之类的逻辑回归算法并不是一个解决复杂非线性问题的好办法。
神经元与大脑
神经网络产生的原因,是人们想尝试设计出模仿大脑的算法,神经网络逐渐兴起于,二十世纪八九十年代,应用得非常广泛,但由于各种原因,在90年代的后期应用减少了,但是最近神经网络,又东山再起了。其中一个原因是,神经网络是计算量有些偏大的算法,然而,大概由于近些年,计算机的运行速度变快,才足以真正运行起大规模的神经网络。
大脑能通过看处理图像,也能帮我们做数学题能帮我们处理各种事情。如果我们想模仿它,那么需要写出不同的软件来模拟大脑做不同事情的方法。不过能不能假设,大脑所做的这些事情不需要成百上千的程序去实现,相反的,大脑处理的方法,只需要一个单一的学习算法就可以了?
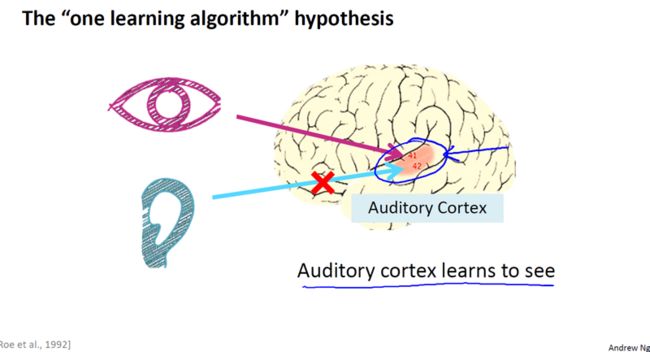
如下图, 图中的片红色区域听觉皮层,我们理解他人说的话靠的是耳朵接收到声音信号并把声音信号传递给你的听觉皮层然后你才能明白我的话。
神经系统科学家做了一个有趣的实验,把耳朵到听觉皮层的神经切断,在这种情况下,将其重新接到一个动物的大脑上,这样从眼睛到视神经的信号最终将传到听觉皮层,如果这样做了,那么结果表明,听觉皮层将会学会“看”,这里“看”代表了,我们所知道的每层含义。所以,如果你对动物这样做,那么动物就可以完成视觉辨别任务,它们可以看图像,并根据图像做出适当的决定,它们正是通过脑组织中的这个部分完成的。
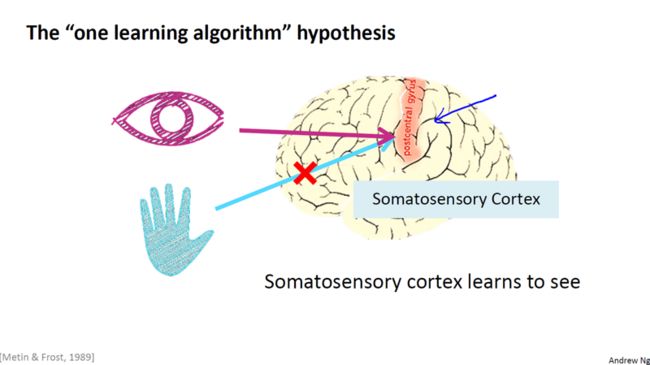
来看另一个例子,图中红色的脑组织是你的躯体感觉皮层,这是你用来处理触觉的如果你做一个和刚才类似的重接实验,那么躯体感觉皮层也能学会”看“、这个实验和其它一些类似的实验被称为神经重接实验。从这个意义上说,如果,人体有同一块,脑组织可以处理光、,声或触觉信号,那么也许存在一种学习算法,可以同时处理,视觉、听觉和触觉,而不是需要,运行上千个不同的程序,或者上千个不同的算法来做这些,大脑所完成的,成千上万的美好事情,也许我们需要做的就是找出,一些近似的或,实际的大脑学习算法,然后实现它,大脑通过自学掌握如何,处理这些不同类型的数据,
从某种意义上来说,如果我们能找出大脑的学习算法,然后在计算机上执行,大脑学习算法或与之相似的算法,也许这将是我们向人工智能迈进做出的最好的尝试,人工智能的梦想就是 有一天能制造出真正的智能机器。
模型展示
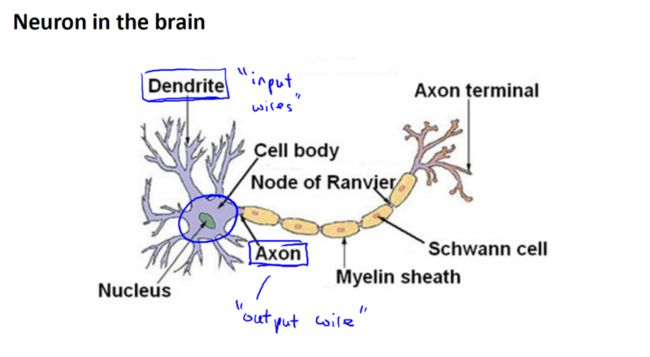
神经网络是在模仿大脑中的神经元或者神经网络时发明的,因此,要解释如何表示模型假设,我们先来看单个 神经元在大脑中是什么样的。
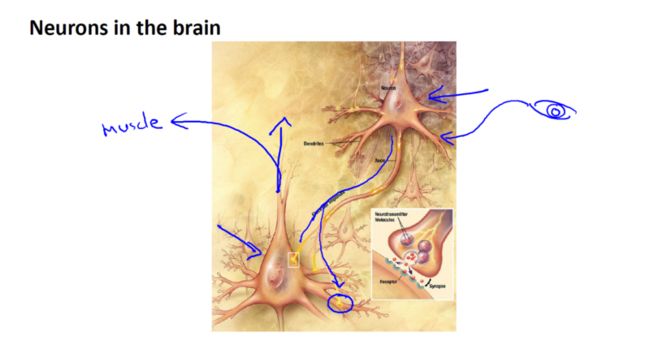
神经元在大脑中,是什么样的,我们的大脑中充满了,这样的神经元,神经元是大脑中的细胞,其中有两点,值得我们注意,一是神经元有,像这样的细胞主体,二是神经元有,一定数量的,输入神经,这些输入神经叫做树突,可以把它们想象成输入电线,它们接收来自其他,神经元的信息,神经元的输出神经叫做轴突,这些输出神经,是用来,给其他神经元传递信号,或者传送信息的,简而言之,神经元是一个计算单元,它从输入神经接受一定数目的信息,并做一些计算,然后将结果通过它的,轴突传送到其他节点,或者大脑中的其他神经元,下面是一组神经元的示意图:
神经元利用微弱的电流进行沟通,这些弱电流也称作动作电位,其实就是一些微弱的电流,所以如果神经元想要传递一个消息,它就会就通过它的轴突发送一段微弱电流给其他神经元,接下来这个神经元接收这条消息做一些计算,它有可能会反过来将在轴突上的自己的消息传给其他神经元,这就是所有,人类思考的模型:我们的神经元把,自己的收到的消息进行计算,并向其他神经元传递消息,顺便说一下,这也是我们的感觉和肌肉运转的原理,如果你想活动一块肌肉,就会触发一个神经元,给你的肌肉发送脉冲,并引起你的肌肉收缩,如果一些感官比如说眼睛,想要给大脑传递一个消息,那么它就像这样发送。
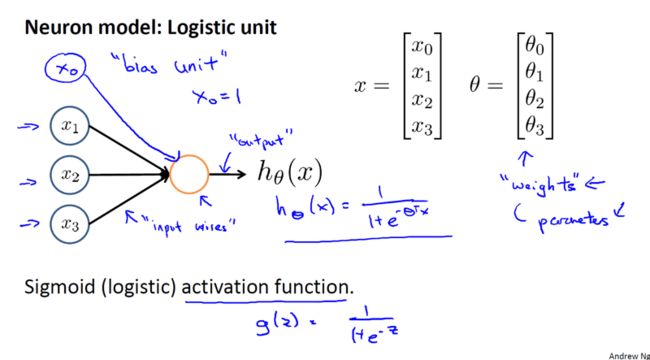
在一个神经网络里,或者说在我们在电脑上实现的人工神经网络里,我们将使用一个非常简单的模型来模拟神经元的工作,我们将神经元模拟成一个逻辑单元。如下图所示,当我画一个这样的,黄色圆圈可以理解为神经元的东西,然后我们通过,它的树突或者说它的输入神经,传递给它一些信息,然后神经元做一些计算,并通过它的输出神经,即它的轴突,输出计算结果。这里的$h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}$。通常x和θ是我们的参数向量,这是一个简单的模型,甚至说是一个过于简单的模拟神经元的模型,它被输入$x_1$,$x_2$和$x_3$,然后输出一些类似这样的结果,绘制一个神经网络时,通常只绘制输入节点$x_1$,$x_2$,$x_3$,但有时也可以增加一个额外的节点$x_0$,这个$x_0$节点有时也被称作偏置单位,或偏置神经元,但因为$x_0$总是等于1,所以有时候会画出它有时不会画出,这取决于它是否对例子有利。
有时我们会说,这是一个神经元,一个有s型函数或者逻辑函数作为激励函数的人工神经元,在神经网络术语中,激励函数只是对类似非线性函数g(z)的另一个术语称呼,$g(z) = \frac{1}{1+e^{-z}}$,到目前为止,我一直称θ为模型的参数,以后大概会继续将这个术语与“参数”相对应,而不是与神经网络,在关于神经网络的文献里,有时你可能会看到人们,谈论一个模型的权重,权重其实和,模型的参数,是一样的东西,,这个小圈,代表一个单一的神经元,神经网络其实就是,这些不同的神经元,组合在一起的集合。
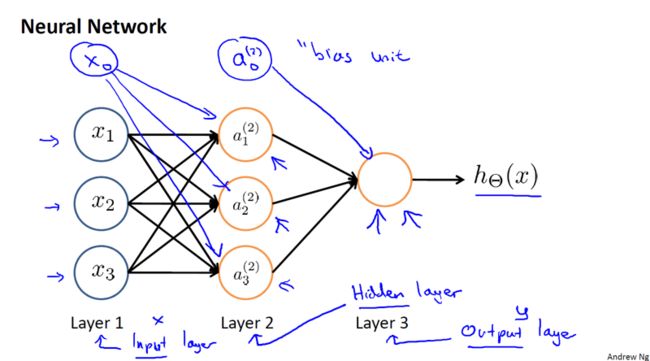
图中,网络中的第一层,也被称为输入层,因为我们在这一层,输入我们的特征项,$x_1$,$x_2$,$x_3$,最后一层,也称为输出层,因为这一层的神经元指的是输出,假设的最终计算结果,中间的两层,也被称作隐藏层,隐藏层不是一个,很合适的术语,但是,直觉上我们知道,在监督学习中,你能看到输入,也能看到正确的输出,而隐藏层的值,你在训练集里是看不到的,它的值不是x,也不是y,所以我们叫它隐藏层,隐藏层也可能不止一个,实际上任何,非输入层或非输出层的层,就被称为隐藏层。
接下来我们逐步分析图表中的计算步骤,首先我们需要解释一些记号:
我要使用a上标(j)下标i表示,第j层的第i个神经元或单元,具体来说,图中比如a上标(2),下标1,表示第2层的第一个激励,即隐藏层的第一个激励,所谓激励(activation),是指由一个具体神经元读入,计算并输出的值。此外,我们的神经网络,被这些矩阵参数化,θ上标(j),它将成为一个波矩阵,控制着从一层,比如说从第一层到第二层或者第二层到第三层的作用。
所以,这就是这张图所表示的计算,比如这里的第一个隐藏单元,是这样计算它的值的,如图中公式所示:$a_1^(2)$等于s函数,作用在这种,第一个公式中输入的线性组合上的结果,第二个隐藏单元,等于s函数作用在这个第二个线性组合上的值,以此类推。在这里,我们有三个输入单元和三个隐藏单元,这样一来,参数矩阵控制了,我们来自三个输入单元三个隐藏单元的映射,因此$\Theta^(1)$的维数,将变成3,$\Theta^(1)$将变成一个3*4维的矩阵,更一般的,如果一个网络在第j层有$s_j$个单元,在j+1层有,$s_{j+1}$个单元,那么矩阵$\Theta^(j)$,即控制第j层到第j+1层映射的矩阵的,维度为$s_{j+1}*(s_j+1)$,所以$\Theta^(j)$的维度是,$s_{j+1}$行,$s_j+1$列。最后,在输出层,我们还有一个单元,它计算h(x),这个也可以,写成$a_1^(3)$就等于后面这块,注意到我这里,写了个上标2,因为$\Theta$上标2,是参数矩阵,或着说是权重矩阵,该矩阵控制从第二层即隐藏层的3个单位到第三层的一个单元,即输出单元的映射。总之,以上我们,展示了像这样一张图是怎样定义一个人工神经网络的,这个神经网络定义了函数h从输入x到输出y的映射,我将这些假设的参数,记为大写的$\Theta$,这样一来,不同的$\Theta$,对应了不同的假设,所以我们有不同的函数,比如说从,x到y的映射。
在上述的式子里,我们将g的部分表达为$z_1^(2)$即$a_1^2 = g(z_1^(2))$,$a_2^2 = g(z_2^(2))$,$a_3^2 = g(z_3^(2))$,所以这些z值都是一个线性组合,是输入值$x_0$,$x_1$,$x_2$,$x_3$的加权线性组合,他将会进入一个特定的神经元。也就是说,对于j=2的第k个节点有:
用向量表示x和$z^j$为:
在上述示例中:
$z^(2) = \Theta^(1)$, $a^(2) = g(z^(2))$,这里的$z^(2)$是个三维向量,$a^(2)$也是个三维向量,因此这里的激励g将sigmod函数逐元素作用于$z^(2)$中的每个元素。这里我们还有隐藏的偏置单元只是未在图中画出,为了注意这额外的偏置单元,我们额外加上一个$a_0^(2) = 1$,这样$a^(2)$就是一个四维特征向量。然后我们为了计算假设的实际输出值,我们只需要计算$z^(3)$,它等于上图中g括号中的部分,$z^(3) = \Theta^(2)a^(2)$,则假设输出$h_\Theta(x) = a^(3) = g(z^(3))$。
这个计算h(x)的过程,也称为前向传播(forward propagation),这样命名是因为我们从输入层的激励开始,然后前向传播给隐藏层并计算隐藏层的激励,然后我们继续前向传播,并计算输出层的激励。这个从输入层到隐藏层再到输入层依次计算激励的过程就叫做前向传播。
定义$x = a^(1)$,我们可以将等式转换成:
这种前向传播的方式,也可以帮助我们理解神经网络的原理和它为什么能够帮助我们学习非线性假设。如下图神经网络,假设我们只看后半部分,也就是从隐藏层到输出层的部分,这看起来就很想逻辑回归。
逻辑回归中,我们用输出层这个节点,即这个逻辑回归单元来预测$h(x)$的值,具体来说,假设函数的等式为:
$$ h_\Theta(x) = g(\Theta_10^2a_0^2+\Theta_11^2a_1^2+\Theta_12^2a_2^2+\Theta_13^2a_3^2) $$
显然这里很像是逻辑回归模型,只是这里的$\Theta$我们用的是大写的。这样做完,我们只得到了逻辑回归,但是逻辑回归的输入特征值是通过隐藏层计算的。它不是使用$x_1$,$x_2$,$x_3$作为输入特征,而是用$a_1$, $a_2$,$a_3$作为新的输入特征。同样我们需要把上标加上来和之前的记号保持一致。有趣的是,特征项$a_1$, $a_2$,$a_3$它们是作为输入的函数来学习的,具体来说,就是从第一层映射到第二层的函数,这个函数由其他 一组参数$\Theta^(1)$决定。所以,在神经网络中它没有使用输入特征$x_1$,$x_2$,$x_3$来训练逻辑回归,而是自己训练逻辑回归的输入$a_1$, $a_2$,$a_3$。可以想象,如果在$\Theta^(1)$中选择不同的参数,有时可以学习到一些很有趣和复杂的特征 就可以得到一个更好的假设,比使用原始输入$x_1$,$x_2$,$x_3$时得到的假设更好。你也可以选择多项式项$x_1$,$x_2$,$x_3$等作为输入项,但这个算法可以灵活地快速学习任意的特征项,把这些$a_1$, $a_2$,$a_3$输入最后的单元,实际上,它就是逻辑回归。
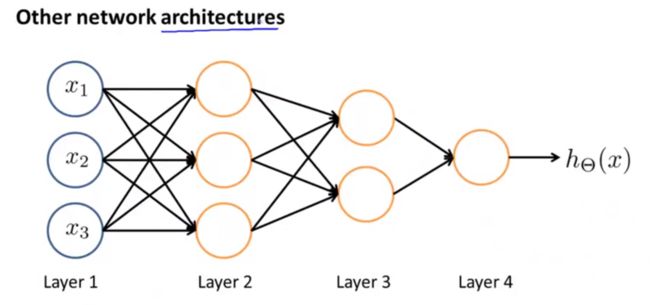
你还可以用其他类型的图来表示神经网络中神经元相连接的方式,称为神经网络的架构,所以说,架构是指,不同的神经元是如何相互连接的,这里有一个不同的,神经网络架构的例子如下图所示:
你可以,意识到这个第二层是如何工作的。在这里,我们有三个隐藏单元,它们根据输入层计算一个复杂的函数,然后第三层可以将第二层训练出的特征项作为输入,并在第三层计算一些更复杂的函数,这样,在你到达输出层之前即第四层,就可以利用第三层训练出的更复杂的特征项作为输入,以此得到非常有趣的非线性假设。顺便说一下,在这样的网络里,第一层被称为输入层,第四层仍然是我们的输出层,这个网络有两个隐藏层,所以,任何一个不是,输入层或输出层的,都被称为隐藏层。
以上,为吴恩达机器学习第四周关于神经网络概念部分的课程笔记。