树状数组与线段树 学习笔记

树状数组与线段树

树状数组

适用问题

• 某个位置上的数加上一个数
• 求某一个前缀和

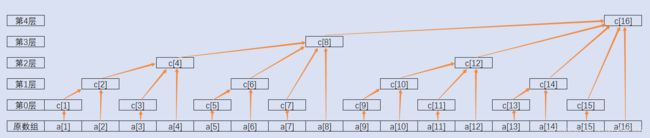
c[x] = (x - lowbit(x), x] = (x - 2^k, x]
//c[x]的值为这个左开右闭区间的元素和, k为x的二进制表示中末尾0的个数, 即c[x]在树状数组中的层数

常用操作及其相应函数

1. 某个位置上的数加上一个数

void add(int x, int v) {
     
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

2. 求某一个前缀和

int query(int x) {
     
    int res = 0;
    for (int i = x; i > 0; i -= lowbit(i)) res += tr[i];
    return res;
}

1264. 动态求连续区间和

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b][a,b] 的连续和。

输入格式：

第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。

第二行包含 n 个整数，表示完整数列。

接下来 m 行，每行包含三个整数 k,a,b（ k=0，表示求子数列[a,b][a,b]的和；k=1，表示第 a 个数加 b）。

数列从 1 开始计数。

输出格式：

输出若干行数字，表示 k=0 时，对应的子数列 [a,b][a,b] 的连续和。

数据范围：

1≤n≤100000,

1≤m≤100000,

1≤a≤b≤n

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

输出样例：

11
30
35

代码：

#include 

using namespace std;
int n, m;
const int N = 100010;
int a[N], tr[N];

int lowbit(int x) {
     
    return x & -x;
}

void add(int x, int v) {
     
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x) {
     
    int res = 0;
    for (int i = x; i > 0; i -= lowbit(i)) res += tr[i];
    return res;
}

int main() {
     
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = 1; i <= n; ++i) add(i, a[i]);
    int c, x, y;
    for (int i = 0; i < m; ++i) {
     
        cin >> c >> x >> y;
        if (c) add(x, y);
        else cout << query(y) - query(x - 1) << endl;
    }
    return 0;
}

线段树

const int N = 100010;
int w[N];
struct Node {
     
    int l, r;
    int sum;
} tr[N * 4];

常用操作

1. 单点修改
2. 区间查询

常用函数

1. 用子节点信息更新当前节点信息

void pushup(int u) {
     
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

2. 在一段区间上初始化线段树

void build(int u, int l, int r) {
     
   if (l == r)tr[u] = {
     l, r, w[r]};
   else {
     
       tr[u] = {
     l, r};
       int mid = (l + r) >> 1;
       build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
       pushup(u);
   }
}

3. 修改

void modify(int u, int x, int v) {
     
    if (tr[u].l == tr[u].r)tr[u].sum += v;
    else {
     
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (x <= mid)modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

4. 查询

int query(int u, int l, int r) {
     
    if (tr[u].l >= l && tr[u].r <= r)return tr[u].sum;
    int mid = (tr[u].l + tr[u].r) >> 1;
    int sum = 0;
    if (l <= mid)sum += query(u << 1, l, r);
    if (r > mid)sum += query(u << 1 | 1, l, r);
    return sum;
}

1270. 数列区间最大值

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式：

第一行两个整数 N,M 表示数字的个数和要询问的次数；

接下来一行为 N 个数；

接下来 M 行，每行都有两个整数 X,Y。

输出格式：

输出共 M 行，每行输出一个数。

数据范围：

1≤N≤105,

1≤M≤106,

1≤X≤Y≤N,

数列中的数字均不超过 2³¹−1

输入样例：

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

输出样例：

5
8

代码：

#include
#include

using namespace std;
int n, m;
const int N = 100010;
int w[N];
struct Node {
     
    int l, r;
    int maxv;
} tr[N * 4];

void pushup(int u) {
     
    tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
}

void build(int u, int l, int r) {
     
    if (l == r)tr[u] = {
     l, r, w[r]};
    else {
     
        tr[u] = {
     l, r};
        int mid = (l + r) >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r) {
     
    if (tr[u].l >= l && tr[u].r <= r)return tr[u].maxv;
    int mid = (tr[u].l + tr[u].r) >> 1;
    int mmax = 0;
    if (l <= mid)mmax = query(u << 1, l, r);
    if (r > mid)mmax = max(mmax, query(u << 1 | 1, l, r));
    return mmax;
}

int main() {
     
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)scanf("%d", &w[i]);
    build(1, 1, n);
    int l, r;
    while (m--) {
     
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }
    return 0;
}