模糊综合评价模型详解

模糊综合评价

“Stay hungry Stay young”

一、问题的引入——量的划分

1. 确定性：经典数学
2. 不确定性：

随机性：概率论，随机过程

灰性：灰色系统

模糊性：模糊数学

二、模糊的概念——模糊集合

2.1 特点

1.模糊集合可以亦次亦彼

例如：{帅，白，高}，不一定帅就不高不白

2.相对于普通集合的特征函数，模糊集合采用了隶属函数的概念
$$u_A:U->[0,1]$$
其中[0,1]中有无数种可能

2.2 表示方法

1. zadeh表示方法
2. 序偶表示法
3. 向量表示法

推荐书籍导读《模糊数学原理及应用》

2.3 分类

一般可以把模糊集合分成三类;

1. 偏小型：年轻，小，冷
2. 中间型：中年，中，暖
3. 偏大型：年老，大，热

三、隶属函数的确定方法

3.1 模糊统计法

原理：找多个人对同一个模糊概念进行描述，用隶属频率去定义隶属度

例如：定义“老年人”的隶属函数，首先找n个人，调查他们对老年人的看法，给出他们认为的年龄区间，对于某一个年龄，例如60，查看n个区间中，包含m的个数，得到60岁年龄的隶属度为m/n，这样通过统计得到各个年龄的隶属度

3.2 借助已有的客观尺度(需要有合适的指标，并能收集到数据)

论域	模糊集	隶属度
设备	设备完好	设备完好率
产品	质量稳定	正品率
家庭	小康家庭	恩格尔系数

注意：这里的指标必须介于0,1之间，如果不是需要进行归一化。

3.3 指派法(根据问题性质，主观的确定隶属函数)

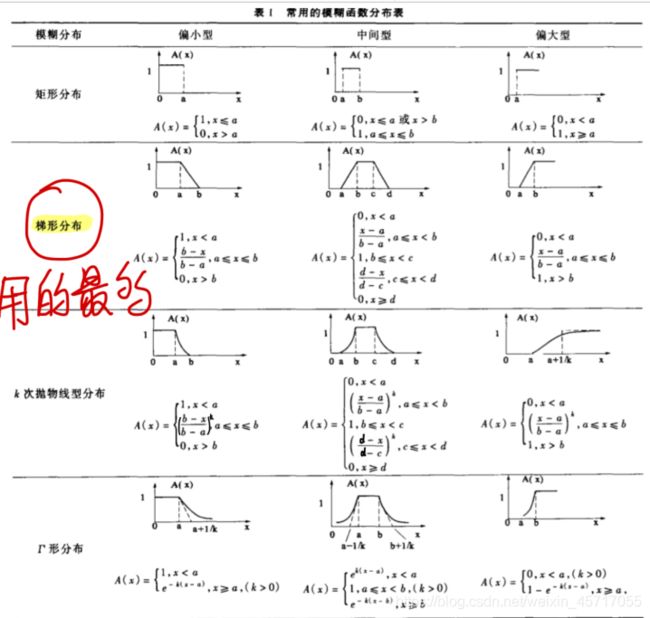
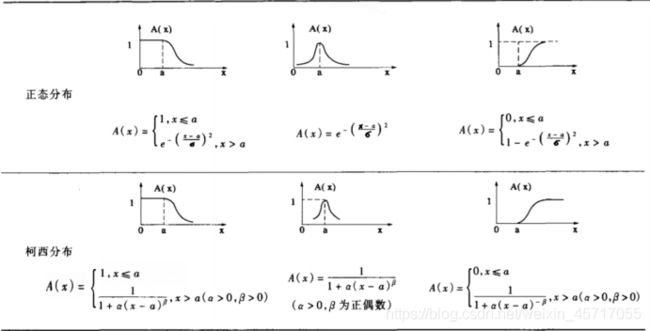
根据问题的性质，直接套用某些分布作为隶属函数，数学建模比赛中常用，但主观性较强

例如柯西分布、矩形分布、梯形分布等等，下图摘自清风老师讲义

四、应用：模糊综合评价（一级模糊综合评价）

应用部分是本节的重点，主要在数学建模中使用

4.1 评价问题概述：

模糊评价问题是要把论域中的对象对应评语集中一个指定的评语或者将方案作为评语集并选择一个最优的方案
在模糊评价问题中，我们引入三个集合

1. 因素集（评价指标集）如U={专业排名、课外实践、志愿服务、竞赛成绩}
2. 评语集（评价的结果）如V={优、良、差}
3. 权重集（指标的标准）如A={0.5,0.1,0.1,0.3}

4.2 一级模糊综合评价模型

当指标个数较少时，一般采用一级模糊综合评价模型，
模型的建立大概有以下步骤，以员工的评价问题为例

4.2.1 确定因素集

对员工的表现，需要从多个方面进行评价，如工作业绩，工作态度，工作能力，沟通能力，政治表现等，所有这些元素构成了评价指标体系集合
记为
U={u1,u2,u3}，在一级综合评价中，n往往较小，且相关性不强

4.2.2 确定评语集

由于每个指标评价的值不同，往往会形成不同的等级，如对工作业绩的评价有好，较好，中等，很差等，这些决断组合成的集合叫做评语集，记为
V={V1,V2,V3}

4.2.3 确定各因素的权重

一般情况下，因素集的各因素在综合评价中所起的作用是不相同的，综合评价的结果不仅与各因素的评价有关，而且很大程度上依赖于各因素对综合评价所起的作用，它是U上的一个模糊向量;
A=[a1,a2,a3]
确定权重的方法有加权平均法，众人评估法等，如果是数学建模问题中可以采用层次分析法

4.2.4 确定模糊综合判断矩阵（重点步骤）

4.2.5 综合评判

以下面例题为例：

这样，得到隶属度最大的是“良好”，为0.53，所以评判结果是良好。

摘自清风老师讲义

注意：隶属函数的构建要经过正向化处理，即隶属度越大越有利。

当指标过多，且指标相关性较强时，可以采用多级模糊评价模型，对评价指标进行分类，更方便我们的考虑。
只需要把每个判断指标看成一级模糊评价模型即可，步骤和一级模糊综合评价大体没有区别。