数学规划详解(附例题及部分Python实现)
数学规划详解(附例题及Python实现)
例题来自于清风老师的数学建模课,个人认为讲的非常好,欢迎大家购买
一、概述
1.1 定义
数学规划是运筹学的一个分支,在约束条件下,按照目标函数来寻求计划管理——>求目标函数在一定约束条件下的极值问题
1.2 一般形式
m i n ( 或 m a x ) z = f ( x ) s . t . ( 限 制 条 件 ) g i ( x ) ≤ 0 , i = 1 , 2 , 3 , , , m ( 不 等 式 约 束 ) min(或max) z=f(x) s.t.(限制条件)g_i(x)\leq0,i=1,2,3,,,m(不等式约束) min(或max)z=f(x)s.t.(限制条件)gi(x)≤0,i=1,2,3,,,m(不等式约束)
称x为决策变量,一般情况下有多个,f(x)为目标函数,约束条件一般有:不等式约束、等式约束、整数约束等等
1.3 分类
-
线性规划(Linear programming):目标函数和与约束条件为决策变量的线性表达式
-
非线性规划(nonlinear programming): 目标函数或约束条件中有一个决策变量是x的非线性表达式
-
整数规划(integar programming ):要求变量取整数的数学规划,目前的整数规划一般也是线性整数规划
-
0-1规划:整数规划的特例,整数变量的取值只能为0和1
二、例题讲解
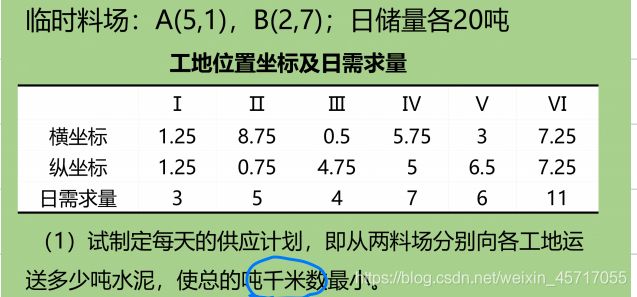
2.1 投料问题(线性规划模型)
假设有两个临时料场,向其他工场运送水泥
列出方程式:
m i n Z = ∑ i = 1 σ ∑ i = 1 δ ( a i − X j ) 2 + ( b i − y j ) 2 min~Z=\sum_{i=1}^\sigma\sum_{i=1}^\delta\sqrt{(a_i-X_j)^2+(b_i-y_j)^2} min Z=i=1∑σi=1∑δ(ai−Xj)2+(bi−yj)2
s . t ∑ j = 1 z X i j ≤ 20 , j = 12 s.t \sum_{j=1}^zX_ij\leq20,j=12 s.tj=1∑zXij≤20,j=12
X i j ≥ 0 , i = 1 , 2 … … 6 , j = 1 , 2 X_ij\geq0,i=1,2……6,j=1,2 Xij≥0,i=1,2……6,j=1,2
这里展示一下如何用python求解这一问题:
这里我选择使用scipy函数,更贴近于MATLAB的操作,当然,也可以使用pulp这个包
from scipy import optimize as op
import numpy as np
import math
a=[1.25,8.75,0.5,5.75,3,7.25]
b=[1.25,0.75,4.75,5,6.5,7.25]
x=[5,2]
y=[1,7]
c=[]
k=0
#计算距离
for j in range(0,2):
for i in range(0,6):
c.append(math.sqrt((a[i]-x[j])**2+(b[i]-y[j])**2))
c=np.array(c)
#不等式约束
A=np.zeros((2,12))
A=np.array([[1,1,1,1,1,1,0,0,0,0,0,0],[0,0,0,0,0,0,1,1,1,1,1,1]])
#不等式约束向量
B=[20,20]
#等式约束
Aeq=np.zeros((6,12))
for i in range(0,6):
Aeq[i,i]=1
Aeq[i,i+6]=1
Beq=np.array([3,5,3,7,6,11])
#每个变量的限制范围
X11=(0,None)
X12=(0,None)
X13=(0,None)
X14=(0,None)
X15=(0,None)
X16=(0,None)
X21=(0,None)
X22=(0,None)
X23=(0,None)
X24=(0,None)
X25=(0,None)
X26=(0,None)
res=op.linprog(c,A,B,Aeq,Beq,bounds=(X11,X12,X13,X14,X15,X16,X21,X22,X23,X24,X25,X26))
print(res)
打印出结果
前六个对应横坐标,后六个元素对应纵坐标
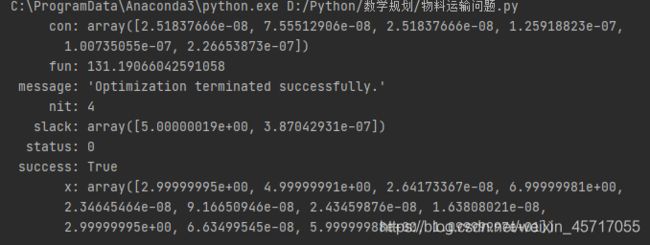
也就是说,第一个料场应该接受约(3,0)的运送量,第二个料场(5,0)以此类推
2.2背包问题(0-1规划问题)
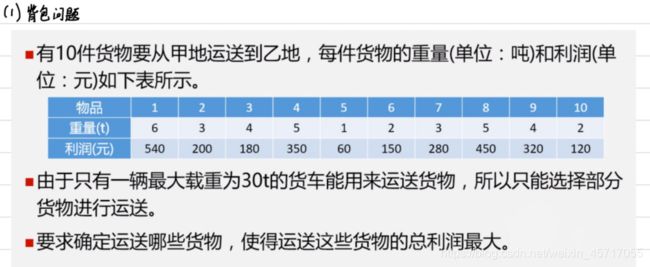
列出方程式:
x = { 1 运 送 了 第 i 件 货 物 0 没 有 运 送 第 i 件 货 物 目 标 函 数 m a x ∑ i = 1 10 p i x i 限 制 条 件 ∑ i = 1 10 w i x i ≤ 30 x ∈ 0 , 1 x= \begin{cases} 1 & 运送了第i件货物\\ 0 & 没有运送第i件货物 \end{cases} \\ \\目标函数 max\sum_{i=1}^{10}p_ix_i \\ 限制条件 \sum_{i=1}^{10}w_ix_i\leq30 \\ x\in{0,1} x={ 10运送了第i件货物没有运送第i件货物目标函数maxi=1∑10pixi限制条件i=1∑10wixi≤30x∈0,1
这里可以采用动态规划的思想求解,也可以采用scipy或者遗传算法求解,这里代码不再展示
2.3 选址问题(非线性规划问题)
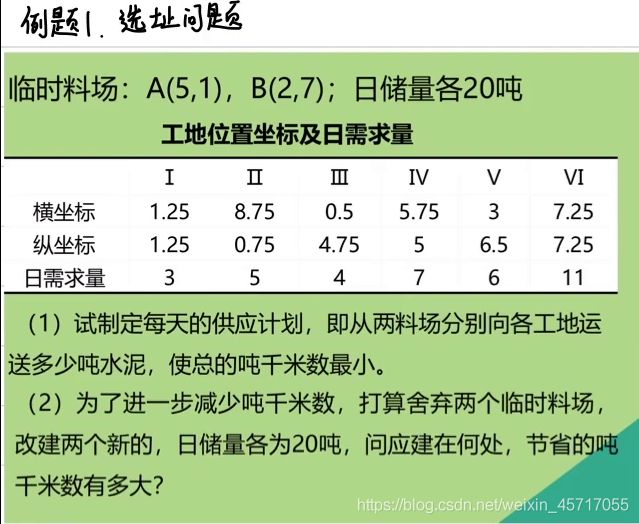
这里其实是在第一问的基础上加了一问,这样就变成了一个非线性规划问题:
列出方程式,求解即可,这里可以使用cxvpy包来求解