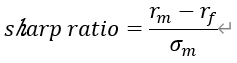马科维茨投资组合有效集、最优投资组合

目的

按照马科维茨的均值方差理论，构建股票的可行集，得到有效前沿，并根据夏普比率获得有效前沿上的最优投资组合，并按照一定的无风险资产配置进行投资，使用测试集检验该种方法的有效程度。

数据来源

1.使用tushare的python数据包。
2.以’300458’, ‘000948’, ‘300327’,‘300735’, '603496’五只股票作为测试。
3.选择2018.1.1-2018.12.31的股票作为训练集，2019.1.1-2019.12.31的股票作为测试集。

理论依据

1.收益的度量：使用日收益率作为证券收益率的随机变量，第t期的日收益率计算公式为：

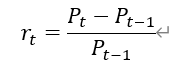
其中为Pt第t期的收盘价，Pt-1为第t-1期的收盘价。
第i种证券的平均收益率表示为：

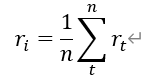
此处使用算术平均的方法求得平均收益率，其中蕴涵了一个假设：过去的每一期收益率发生的概率是相等的。（在无法得知过去收益率分布的情况下可据此近似计算，或采用几何平均的计算方法）

2.风险的度量：使用证券日收益率的波动程度表示证券的风险，即证券日收益率的标准差，第i种证券的标准差计算公式为：

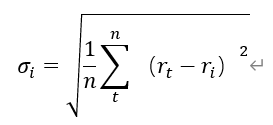
3.约束条件：构建投资组合的可行集应该满足一下三个约束条件：

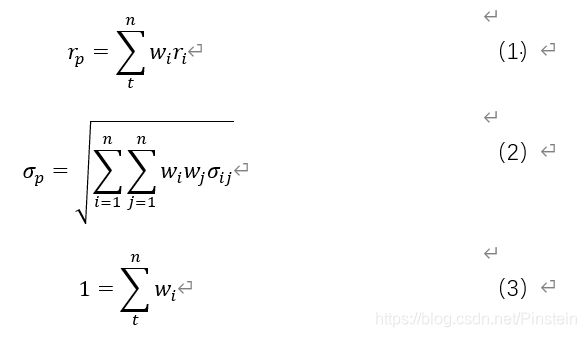
式（1）表示投资组合的收益率；

式（2）表示投资组合的风险，表示第种证券和第种证券的协方差；

式（3）表示不允许卖空的情况下，所有证券的持有比例加起来为1.

过程

1.两只股票的情形

使用’300735’,和’603496’两只股票构建投资组合，绘制组合的“收益-风险“图形如下：

图1

2.五只股票的情形
使用’300458’,‘000948’, ‘300327’, ‘300735’, '603496’五只股票构建投资组合，绘制其可行集如下：

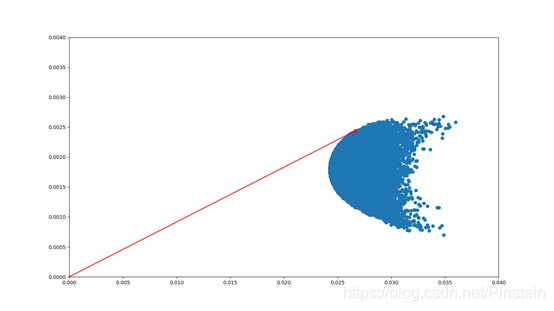
图2
对比图1和图2可看出，当投资组合中证券数量增多时，收益率不仅没有下降，风险还随之减少了。

根据马科维茨的理论，我们可以选取的投资组合位于有效前沿上。为了进一步筛选有效前沿上的投资组合，我们采用夏普比率进行筛选，取有效前沿上的夏普比率最高的投资组合为最佳投资组合。夏普比率计算公式如下所示：

其中为投资组合的收益率，无风险资产的收益率，我们假设不持有无风险资产，则夏普比率变为：

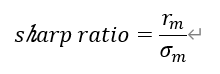
由夏普比率可绘制资本市场线（CML）如图2红线所示，红点处即为夏普比率最高的投资组合

#股票的相关系数、收益率的均值和方差

import tushare as ts
import pandas as pd
import math

def get_yield_rate(code, Start, End):   #获取股票的单期收益率
    df = ts.get_hist_data(code, start=Start, end=End) #从接口获取股票数据
    close = df['close'] #收盘价
    lagclose = close.shift(-1)  #让收盘价滞后-1期
    yield_rate = (close-lagclose)/lagclose  #计算单期收益率
    yield_rate.name = 'yield_rate'  #给series设置名字
    yield_rate = pd.DataFrame(yield_rate)   #将series变为DataFrame
    yield_rate = yield_rate.fillna(method='backfill', axis=0)  #向上填充列
    yield_rate = yield_rate.fillna(method='ffill', axis=0)     #向下填充列
    return yield_rate

def EX(yield_rate): #计算收益率的均值
    result = 0
    for i in yield_rate.index:
        result = result + yield_rate.loc[i, 'yield_rate']
    mean_value = result/len(yield_rate)
    return mean_value
def X_EX(yield_rate):   #计算X-EX
    mean_value = EX(yield_rate)
    yield_rate['mean_value'] = mean_value
    result = yield_rate['yield_rate'] - yield_rate['mean_value']
    return result
def CovXY(yield_rate1, yield_rate2):    #计算Cov(X,Y)
    x_Ex = X_EX(yield_rate1)
    y_Ey = X_EX(yield_rate2)
    result = x_Ex * y_Ey
    result.name = '(X-EX)(Y-EY)'
    result = pd.DataFrame(result)
    mean = 0
    for i in result.index:
        mean = mean + result.loc[i, '(X-EX)(Y-EY)']
    Cov = mean/len(yield_rate1)
    return Cov
def DX(yield_rate): #计算方差
    x_Ex = X_EX(yield_rate)
    x_Ex2 = x_Ex * x_Ex
    x_Ex2.name = '(X-EX)^2'
    x_Ex2 = pd.DataFrame(x_Ex2)
    result = 0
    for i in x_Ex2.index:
        result = result + x_Ex2.loc[i, '(X-EX)^2']
    Dx = result/len(yield_rate)
    return Dx
def ruo(code1, code2, Start, End):
    yield_rate1 = get_yield_rate(code1, Start, End)
    yield_rate2 = get_yield_rate(code2, Start, End)
    Cov = CovXY(yield_rate1, yield_rate2)
    Dx = DX(yield_rate1)
    Dy = DX(yield_rate2)
    R = Cov/((math.sqrt(Dx))*math.sqrt(Dy))
    return R


def get_EX(code, Start, End):   #返回均值
    yield_rate = get_yield_rate(code, Start, End)
    Ex = EX(yield_rate)
    return Ex
def get_DX(code, Start, End):   #返回方差
    yield_rate = get_yield_rate(code, Start, End)
    Dx = DX(yield_rate)
    return Dx

#股票的相关系数矩阵

import security_data
import pandas as pd

def get_ruo(list, Start, End):  #建立相关系数矩阵
    ruo_df = pd.DataFrame()
    for i in list:
        ruo_df.loc[i, ] = 0
        for j in list:
            ruo = security_data.ruo(i, j, Start, End)
            ruo_df.loc[i, j] = ruo
    return ruo_df
def get_Ex_Dx(list, Start, End):    #计算均值和方差
    Ex_Dx_df = pd.DataFrame()
    for i in list:
        Ex = security_data.get_EX(i, Start, End)
        Dx = security_data.get_DX(i, Start, End)
        Ex_Dx_df.loc[i, 'EX'] = Ex
        Ex_Dx_df.loc[i, 'DX'] =Dx
    return Ex_Dx_df


def get_correlation_matrix(Start, End, security_list):
    ruo_df = get_ruo(security_list, Start, End)
    Ex_Dx_df = get_Ex_Dx(security_list, Start, End)
    return ruo_df, Ex_Dx_df

#比较股票的相关系数

import security_data as sd
import tushare as ts
import pandas as pd

def get_code():
    code_list = []
    df = ts.get_sz50s()
    for i in df.loc[:, 'code']:
        code_list.append(i)
    return code_list
def get_ruo(Start, End):
    ruo_df = pd.DataFrame()
    code_list = get_code()
    for i in code_list:
        for j in code_list:
            ruo = sd.ruo(i, j, Start, End)
            if ruo <= 0:
                ruo_df.loc[i, j] = ruo
                print(i, j, ruo_df.loc[i, j])
    return ruo_df



Start = '2019-01-01'
End = '2019-12-24'
ruo_df = get_ruo(Start, End)
print(ruo_df)

#绘制两两股票的有效边界

import correlation as cor
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
import tushare as ts


def effecient_set(r1, r2, D1, D2, ruo_12):  #绘制两只股票的有效边界
    x = []
    y = []
    if r1 > r2:
        a = np.linspace(r2, r1, 50)
    else:
        a = np.linspace(r1, r2, 50)
    for i in a:
        x.append(i)
        y.append((math.sqrt(math.pow(((i - r2) * math.sqrt(D1) + (r1 - i) * math.sqrt(D2)), 2) +
                            2 * (i - r2) * (r1 - i) * (ruo_12 - 1) * math.sqrt(D1) * math.sqrt(D2))) \
                 / abs(r1 - r2))
    plt.plot(y, x)

def begin(Start, End):
    code_list = []
    df = ts.get_sz50s()
    for i in df.loc[:, 'code']:
        code_list.append(i)
    ruo_df, Ex_Dx_df = cor.get_correlation_matrix(Start, End, code_list)
    plt.figure()
    for i in range(len(code_list)-1):
        for j in range(len(code_list)-i-1):
            r1 = Ex_Dx_df.loc[code_list[i], 'EX']
            r2 = Ex_Dx_df.loc[code_list[i+j+1], 'EX']
            D1 = Ex_Dx_df.loc[code_list[i], 'DX']
            D2 = Ex_Dx_df.loc[code_list[i+j+1], 'DX']
            ruo_12 = ruo_df.loc[code_list[i], code_list[i+j+1]]
            effecient_set(r1, r2, D1, D2, ruo_12)
    plt.show()

Start = '2019-01-01'
End = '2019-12-24'
begin(Start, End)

#有效前沿 effciency_set

import correlation as cor
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
import tushare as ts
import random
import time

def get_original_weight(number):   #获得50只股票的随机权重
    x = np.random.rand(number)
    ratio = 1/sum(x)
    x = x * ratio
    x = list(x)
    return x

def get_rp(weight, Ex_Dx_df):   #计算总收益率
    rp = 0
    count = 0
    for i in Ex_Dx_df.index:
        rp = rp + Ex_Dx_df.loc[i, 'EX'] * weight[count]
        count = count + 1
    return rp

def get_sgm_p(weight, ruo_df, Ex_Dx_df):    #计算总风险
    sgm_p = 0
    count1 = -1
    for i in Ex_Dx_df.index:
        count1 = count1 + 1
        weight1 = weight[count1]
        sgm1 = math.sqrt(Ex_Dx_df.loc[i, 'DX'])
        count2 = -1
        for j in Ex_Dx_df.index:
            count2 = count2 + 1
            weight2 = weight[count2]
            sgm2 = math.sqrt(Ex_Dx_df.loc[j, 'DX'])
            ruo12 = ruo_df.loc[i, j]
            sgm_p = sgm_p + weight1 * weight2 * sgm1 * sgm2 * ruo12
    return math.sqrt(sgm_p)

def plot_CML(sgm_i, sharp_ratio):
    x = []
    y = []
    a = np.linspace(0, sgm_i, 50)
    for i in a:
        x.append(i)
        y.append(i * sharp_ratio)
    plt.plot(x, y, c='r')

def get_weight(Start, End, code_list, portfolio_number):
    x = []
    y = []
    sharp_ratio = 0
    ruo_df, Ex_Dx_df = cor.get_correlation_matrix(Start, End, code_list)
    for i in range(portfolio_number):
        weight = get_original_weight(len(code_list))
        rp = get_rp(weight, Ex_Dx_df)
        sgm_p = get_sgm_p(weight, ruo_df, Ex_Dx_df)
        y.append(rp)
        x.append(sgm_p)
        sharp_ratio_temp = rp / sgm_p
        if sharp_ratio_temp > sharp_ratio:
            sharp_ratio = sharp_ratio_temp
            ri = rp
            sgm_i = sgm_p
            weight_final = weight

    plt.figure()
    plt.xlim([0, 0.04])  # 设置绘图X边界
    plt.ylim([0, 0.004])
    plt.scatter(x, y)
    plot_CML(sgm_i, sharp_ratio)
    plt.scatter(sgm_i, ri)
    plt.show()
    print('ri:', ri, 'sgm_i:', sgm_i)
    print('weight:', weight_final)


start = time.clock()


Start = '2018-01-01'
End = '2018-12-31'
code_list = ['300458', '000948', '300327', '300735', '603496']
get_weight(Start, End, code_list, 1000000)



elapsed = (time.clock() - start)
print("Time used:",elapsed)


#ri_19 = 0.002507473327125009
#sgm_i_19 = 0.027271707336635868
#weight_19: [0.560259898457182, 0.0011445939423587268, 0.18022505839139358, 0.25549792575307023, 0.0028725234559953145]

#ri_18: 0.0007537633778995758 sgm_i_18: 0.03786930749207172
#weight_18: [0.005199184879159315, 0.01004921278630503, 0.0032974530547201057, 0.9789594590449071, 0.0024946902349084646]
list = ['600000', '600009', '600016', '600028', '600030', '600031', '600036', '600048', '600050', '600104', '600196', '600276', '600309', '600340', '600519', '600547', '600585', '600690', '600703', '600837', '600887', '601012', '601066', '601088', '601111', '601138', '601166', '601186', '601211', '601236', '601288', '601318', '601319', '601328', '601336', '601390', '601398', '601601', '601628', '601668', '601688', '601766', '601818', '601857', '601888', '601939', '601988', '601989', '603259', '603993']

#测试投资组合收益率 test_set


import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
import tushare as ts
import random
import time
#import efficiency_set as es
import security_data as sd


def test(code_list, Start, End):
    return_all = []
    #weight = es.get_weight(Start, End, code_list, portfolio_number)
    weight = [0.005199184879159315, 0.01004921278630503, 0.0032974530547201057, 0.9789594590449071, 0.0024946902349084646]
    for c in range(len(code_list)):
        yield_rate = sd.get_yield_rate(code_list[c], Start, End)
        return_item = 1
        for i in yield_rate.index:
            return_item = return_item * (1 + yield_rate.loc[i, 'yield_rate'])
        return_item = return_item * weight[c]
        return_all.append(return_item)
    print(return_all)
    sum = 0
    for i in return_all:
        sum = sum + i
    print('sum:', sum)


Start = '2019-01-01'
End = '2019-12-31'
code_list = ['300458', '000948', '300327', '300735', '603496']
test(code_list, Start, End)

#capm模型分析股票收益率 capm

import tushare as ts
import pandas as pd
import numpy as np
import security_data as sd
import time

def get_yield_rate(code, Start, End):   #获取股票的单期收益率
    df = ts.get_hist_data(code, start=Start, end=End) #从接口获取股票数据
    close = df['close'] #收盘价
    lagclose = close.shift(-1)  #让收盘价滞后-1期
    yield_rate_series = (close-lagclose)/lagclose  #计算单期收益率
    yield_rate_series.name = 'yield_rate'  # 给series设置名字
    yield_rate_df = pd.DataFrame(yield_rate_series)  # 将series变为DataFrame
    yield_rate_df = yield_rate_df.fillna(method='backfill', axis=0)  # 向上填充列
    yield_rate_df = yield_rate_df.fillna(method='ffill', axis = 0)  # 向下填充列
    return yield_rate_df

#以沪深300构建市场组合
def get_market_portfolio(Start, End):
    hs300_df = ts.get_hs300s()
    code_list = []  #储存沪深300的股票代码
    weight = [] #储存沪深300的股票权重
    yield_rate_init = pd.DataFrame()
    for i in hs300_df.loc[:, 'code']:
        code_list.append(i)
    for i in hs300_df.loc[:, 'weight']:
        weight.append(i)
    M_yield_rate = get_yield_rate(code_list[0], Start, End)
    M_yield_rate.loc[:, 'yield_rate'] = 0   #初始化市场组合M日收益率
    for code_number in range(len(code_list)):
        yield_rate = get_yield_rate(code_list[code_number], Start, End)
        M_yield_rate = pd.merge(M_yield_rate, yield_rate, how='left', on='date')
        M_yield_rate = M_yield_rate.fillna(method='backfill', axis=0)  # 向上填充列
        M_yield_rate = M_yield_rate.fillna(method='ffill', axis=0)  # 向下填充列
        M_yield_rate = M_yield_rate.fillna(0)  # 若存在股票尚未上市的情况，用0填充所有收益率
        yield_rate_init['yield_rate'] = M_yield_rate.loc[:, 'yield_rate_x'] + weight[code_number]*M_yield_rate.loc[:, 'yield_rate_y']
        M_yield_rate = yield_rate_init
        yield_rate_init = pd.DataFrame()
    return M_yield_rate

time_start = time.clock()



Start = '2018-01-01'
End = '2018-12-31'
code = '600000'
item_yield_rate = get_yield_rate(code, Start, End)
M_yield_rate = get_market_portfolio(Start, End)
Cov = sd.CovXY(M_yield_rate, item_yield_rate)
Dm = sd.DX(M_yield_rate)
rm = sd.EX(M_yield_rate)
ri = (Cov/Dm)*rm
print(ri)



elapsed = (time.clock() - time_start)
print("Time used:", elapsed)