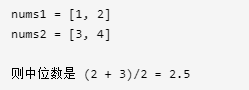二分-LeetCode4. 寻找两个正序数组的中位数+两个有序数组中找第k小的数

1、题目描述

https://leetcode-cn.com/problems/median-of-two-sorted-arrays/

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。  

请你找出这两个正序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。  

你可以假设 nums1 和 nums2 不会同时为空。

2、代码详解

https://mp.weixin.qq.com/s/FBlH7o-ssj_iMEPLcvsY2w

二分查找，所以现在要做的就是在两个排序数组中进行二分查找。  将问题 转化为在两个数组中找第 K 个小的数 。求中位数，其实就是求第 k 小数的一种特殊情况。

首先在两个数组中分别找出第 k/2 大的数，再比较这两个第 k/2 大的数，假设两个数组为 A ，B。比较结果会有下面几种情况：

1. A[k/2] = B[k/2],那么第 k 大的数就是 A[k/2]

2. A[k/2] > B[k/2],那么第 k 大的数肯定在 A[0:k/2+1] 和 B[k/2:] 中，这样就将原来的所有数的总和减少到一半了，再在这个范围里面找第 k/2 大的数即可，这样也达到了二分查找的区别了。

3. A[k/2] < B[k/2]，那么第 k 大的数肯定在 B[0:k/2+1]和 A[k/2:] 中，同理在这个范围找第 k/2 大的数就可以了。

 

• 时间复杂度：每进行一次循环，减少 k/2 个元素，所以时间复杂度是 O(log(k)），而 k = (m+n) / 2，所以最终的复杂也就是 O(log(m+n）。  
• 空间复杂度：虽然用到了递归，但是可以看到这个递归属于尾递归，所以编译器不需要不停地堆栈，所以空间复杂度为 O(1)。

class Solution(object):
    def findMedianSortedArrays(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: float
        """
        # 时间复杂度为 O(log(m+n))，在两个排序数组中进行二分查找
        # 将问题转化为在两个数组中找第 K 个小的数
        n = len(nums1)
        m = len(nums2)

        left = (n+m+1)//2
        right = (n+m+2)//2
        # 将偶数和奇数的情况合并，如果是奇数，会求两次同样的 k
        return 0.5 * (self.getKth(nums1, 0, n-1, nums2, 0, m-1, left)
                      + self.getKth(nums1, 0, n-1, nums2, 0, m-1, right))

    def getKth(self, nums1, start1, end1, nums2, start2, end2, k):
        len1 = end1 - start1 + 1
        len2 = end2 - start2 + 1
        # 让 len1 的长度小于 len2，这样就能保证如果有数组空了，一定是 len1
        if len1 > len2:
            return self.getKth(nums2, start2, end2, nums1, start1, end1, k)
        if len1 == 0:
            return nums2[start2 + k - 1]  # 处理特殊情况, nums2[k - 1]
        if k == 1:
            return min(nums1[start1], nums2[start2])

        # 分别取 k/2-1 位
        i = start1 + min(len1, k//2) - 1  # 数组下标从0开始，-1
        j = start2 + min(len2, k//2) - 1
        # A[k/2] = B[k/2],那么第 k 大的数就是 A[k/2]

        # A[k/2] > B[k/2],那么第 k 大的数肯定在 A[0:k/2+1] 和 B[k/2:] 中，
        # 这样就将原来的所有数的总和减少到一半了，再在这个范围里面找第 k/2 大的数

        # A[k/2] < B[k/2]，那么第 k 大的数肯定在 B[0:k/2+1]和 A[k/2:] 中，
        # 同理在这个范围找第 k/2 大的数

        if nums1[i] > nums2[j]:
            return self.getKth(nums1, start1, end1, nums2, j+1, end2, k - (j-start2+1))
        else:
            return self.getKth(nums1, i+1, end1, nums2, start2, end2, k - (i-start1+1))




nums1 = [1, 2]
nums2 = [3, 4]
s = Solution()
print(s.findMedianSortedArrays(nums1, nums2))

多解法：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-2/

拓展：两个有序数组中找第k小的数

# O(log(min(len(m),len(n)))
s = Solution()
m = [1,2,2,7]
n = [3,4,5]
k = 5
print(s.findMinK(m, n, k))  # 4

参考左神思路

# 寻找两个有序数组中第k小
# @param m 数组
# @param n 数组
# @param k int
# @return int
class Solution:
    def findMinK(self, m, n, k):
        def get_median(a1, s1, e1, a2, s2, e2):
            while s1 < e1:
                mid1 = (s1+e1)//2
                mid2 = (s2+e2)//2
                p = (e1 - s1 + 1) & 1 ^ 1  # offset 元素个数为奇数，p=0，为偶数p=1
                if a1[mid1] == a2[mid2]:
                    return a1[mid1]
                elif a1[mid1] > a2[mid2]:
                    e1 = mid1
                    s2 = mid2 + p
                else:
                    s1 = mid1 + p
                    e2 = mid2
            return min(a1[s1], a2[s2])
        if len(m) > len(n):
            long = m
            short = n
        else:
            short = m
            long = n
        l = len(long)
        s = len(short)
        if k <= s:
            return get_median(short, 0, k-1, long, 0, k-1)
        if k > l:
            if long[k-s-1] >= short[-1]:
                return long[k-s-1]
            if short[k-l-1] >= long[-1]:
                return short[k-l-1]
            return get_median(long, k-s, l-1, short, k-l, s-1)
        if long[k-s-1] >= short[-1]:
            return long[k-s-1]
        return get_median(long, k-s, k-1, short, 0, s-1)

https://www.cnblogs.com/pathjh/p/9096652.html