python统计分布和概率_Python基本统计信息:概率
python统计分布和概率
When studying statistics, you will inevitably have to learn about probability. It is easy lose yourself in the formulas and theory behind probability, but it has essential uses in both working and daily life. We’ve previously discussed some basic concepts in descriptive statistics; now we’ll explore how statistics relates to probability.
在研究统计数据时,您将不可避免地要学习概率。 在概率背后的公式和理论中很容易迷失自己,但它在工作和日常生活中都有必不可少的用途。 前面我们已经讨论了描述统计中的一些基本概念; 现在,我们将探讨统计学与概率的关系。
先决条件: (Prerequisites:)
Similar to the previous post, this article assumes no prior knowledge of statistics, but does require at least a general knowledge of Python. If you are uncomfortable with for loops and lists, I recommend covering them briefly before progressing.
与上一篇文章类似,本文假定没有先验统计知识,但至少需要具备Python的一般知识。 如果您对for循环和列表不满意 ,建议您在进行操作之前简要介绍一下它们。
概率是多少? (What is probability?)
At the most basic level, probability seeks to answer the question, “What is the chance of an event happening?” An event is some outcome of interest. To calculate the chance of an event happening, we also need to consider all the other events that can occur.
在最基本的层面上,概率试图回答以下问题:“事件发生的机会是什么?” 事件是一些令人感兴趣的结果。 要计算事件发生的机会,我们还需要考虑所有可能发生的其他事件。
The quintessential representation of probability is the humble coin toss. In a coin toss the only events that can happen are:
概率的典型代表是谦虚的抛硬币。 在抛硬币中,唯一可能发生的事件是:
- Flipping a heads
- Flipping a tails
- 翻转头
- 翻转尾巴
These two events form the sample space, the set of all possible events that can happen. To calculate the probability of an event occurring, we count how many times are event of interest can occur (say flipping heads) and dividing it by the sample space. Thus, probability will tell us that an ideal coin will have a 1-in-2 chance of being heads or tails. By looking at the events that can occur, probability gives us a framework for making predictions about how often events will happen.
这两个事件构成了示例空间 ,即所有可能发生的事件的集合。 为了计算事件发生的概率,我们计算感兴趣事件可以发生多少次(例如翻转),然后将其除以样本空间。 因此,概率将告诉我们,理想的硬币正面或反面的几率将为1比2。 通过查看可能发生的事件,概率为我们提供了一个框架,用于预测事件的发生频率。
However, even though it seems obvious, if we actually try to toss some coins, we’re likely to get an abnormally high or low counts of heads every once in a while. If we don’t want to make the assumption that the coin is fair, what can we do? We can gather data! We can use statistics to calculate probabilities based on observations from the real world and check how it compares to the ideal.
但是,即使看起来很明显,但如果我们实际上尝试扔掉一些硬币,偶尔也会有一次异常高或低的正面计数。 如果我们不想以为硬币是公平的,该怎么办? 我们可以收集数据! 我们可以使用统计数据基于对现实世界的观察来计算概率,并检查其与理想情况的比较。
从统计到概率 (From statistics to probability)
Our data will be generated by flipping a coin 10 times and counting how many times we get heads. We will call a set of 10 coin tosses a trial. Our data point will be the number of heads we observe. We may not get the “ideal” 5 heads, but we won’t worry too much since one trial is only one data point.
我们的数据将通过掷硬币10次并计数我们获得多少次来生成。 我们将召集一组10个抛硬币试验。 我们的数据点将是我们观察到的磁头数量。 我们可能没有“理想”的5个方面,但是我们不会担心太多,因为一次试验只是一个数据点。
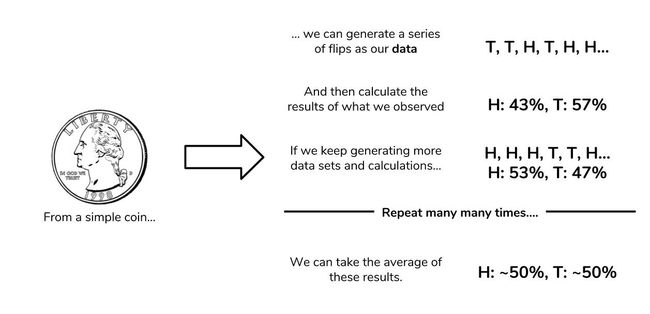
If we perform many, many trials, we expect the average number of heads over all of our trials to approach the 50%. The code below simulates 10, 100, 1000, and 1000000 trials, and then calculates the average proportion of heads observed. Our process is summarized in the image below as well.
如果我们进行许多次试验,我们希望所有试验中的平均主管人数接近50%。 下面的代码模拟10、100、1000和1000000次试验,然后计算观察到的头部的平均比例。 下图也总结了我们的过程。
import random def coin_trial(): heads = 0 for i in range(100): if random.random() <= 0.5: heads +=1 return heads def simulate(n): trials = [] for i in range(n): trials.append(coin_trial()) return(sum(trials)/n) simulate(10) >> 5.4 simulate(100) >>> 4.83 simulate(1000) >>> 5.055 simulate(1000000) >>> 4.999781import random def coin_trial(): heads = 0 for i in range(100): if random.random() <= 0.5: heads +=1 return heads def simulate(n): trials = [] for i in range(n): trials.append(coin_trial()) return(sum(trials)/n) simulate(10) >> 5.4 simulate(100) >>> 4.83 simulate(1000) >>> 5.055 simulate(1000000) >>> 4.999781
The coin_trial function is what represents a simulation of 10 coin tosses. It uses the random() function to generate a float between 0 and 1, and increments our heads count if it’s within half of that range. Then, simulate repeats these trials depending on how many times you’d like, returning the average number of heads across all of the trials.
coin_trial函数代表10次coin_trial硬币的模拟。 它使用random()函数生成介于0和1之间的浮点数,如果它在该范围的一半以内,则会增加我们的heads计数。 然后, simulate根据您想要的次数重复这些试验,并返回所有试验中的平均水头数。
The coin toss simulations give us some interesting results. First, the data confirm that our average number of heads does approach what probability suggests it should be. Furthermore, this average improves with more trials. In 10 trials, there’s some slight error, but this error almost disappears entirely with 1,000,000 trials. As we get more trials, the deviation away from the average decreases. Sound familiar?
投币模拟给了我们一些有趣的结果。 首先,数据证实我们的平均正面人数确实接近了应有的概率。 此外,随着更多的试验,该平均值得到提高。 在10个试验中,有一些轻微的错误,但是在进行1,000,000次试验后,该错误几乎完全消失了。 随着更多的试验,偏离平均值的偏差减小。 听起来有点熟?
Sure, we could have flipped the coin ourselves, but Python saves us a lot of time by allowing us to model this process in code. As we get more and more data, the real-world starts to resemble the ideal. Thus, given enough data, statistics enables us to calculate probabilities using real-world observations. Probability provides the theory, while statistics provides the tools to test that theory using data. The descriptive statistics, specifically mean and standard deviation, become the proxies for the theoretical.
当然,我们本来可以扔掉硬币的,但是Python通过允许我们在代码中对该过程进行建模,为我们节省了很多时间。 随着我们获得越来越多的数据,现实世界开始类似于理想状态。 因此,在给定足够的数据的情况下,统计数据使我们能够使用实际观察值来计算概率。 概率提供了理论,而统计学提供了使用数据测试该理论的工具。 描述性统计,特别是均值和标准差,成为理论上的代理。
You may ask, “Why would I need a proxy if I can just calculate the theoretical probability itself?” Coin tosses are a simple toy example, but the more interesting probabilities are not so easily calculated. What is the chance of someone developing a disease over time? What is the probability that a critical car component will fail when you are driving?
您可能会问:“如果我仅能自己计算理论概率,那为什么我需要代理?” 抛硬币是一个简单的玩具示例,但更有趣的概率却不那么容易计算。 随着时间的推移,某人患上疾病的机会有多大? 开车时关键的汽车部件发生故障的概率是多少?
There are no easy ways to calculate probabilities, so we must fall back on using data and statistics to calculate them. Given more and more data, we can become more confident that what we calculate represents the true probability of these important events happening.
没有简单的方法来计算概率,因此我们必须依靠数据和统计数据来计算它们。 在提供越来越多的数据的情况下,我们可以更加放心,我们计算出的值代表了这些重要事件发生的真实概率。
That being said, remember from our previous statistics post that you are a sommelier-in-training. You need to figure out which wines are better than others before you start purchasing them. You have a lot of data on hand, so we’ll use our statistics to guide our decision.
话虽这么说,但请记住,根据我们以前的统计信息 ,您是一位培训侍酒师。 在开始购买葡萄酒之前,您需要确定哪些葡萄酒比其他葡萄酒更好。 您手头上有很多数据,因此我们将使用我们的统计数据来指导我们的决策。
数据与分布 (The data and the distribution)
Before we can tackle the question of “which wine is better than average,” we have to mind the nature of our data. Intuitively, we’d like to use the scores of the wines to compare groups, but there comes a problem: the scores usually fall in a range. How do we compare groups of scores between types of wines and know with some degree of certainty that one is better than the other?
在解决“哪种葡萄酒比平均水平更好”的问题之前,我们必须考虑数据的性质。 直观地讲,我们想用葡萄酒的分数来比较各组,但是有一个问题:分数通常在一定范围内。 我们如何比较葡萄酒类型之间的分数组,并在一定程度上确定一种葡萄酒优于另一种葡萄酒?
Enter the normal distribution. The normal distribution refers to a particularly important phenomenon in the realm of probability and statistics. The normal distribution looks like this:
输入正态分布。 正态分布是指概率和统计领域中的一个特别重要的现象。 正态分布如下所示:
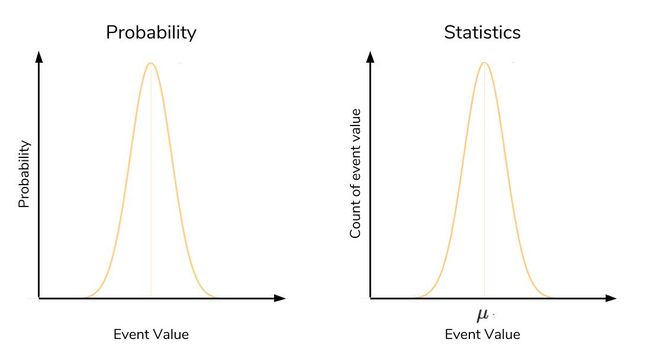
The most important qualities to notice about the normal distribution is its symmetry and its shape. We’ve been calling it a distribution, but what exactly is being distributed? It depends on the context.
关于正态分布要注意的最重要性质是其对称性和形状 。 我们一直称其为分布,但实际上分布的是什么? 这取决于上下文。
In probability, the normal distribution is a particular distribution of the probability across all of the events. The x-axis takes on the values of events we want to know the probability of. The y-axis is the probability associated with each event, from 0 to 1. We haven’t discussed probability distributions in-depth here, but know that the normal distribution is a particularly important kind of probability distribution.
在概率上,正态分布是所有事件之间概率的特定分布。 x轴代表我们想知道概率的事件的值。 y轴是与每个事件相关的概率,范围是0到1。我们在这里没有深入讨论概率分布,但是知道正态分布是一种特别重要的概率分布。
In statistics, it is the values of our data that are being distributed. Here, the x-axis is the values of our data, and the y-axis is the count of each of these values. Here’s the same picture of the normal distribution, but labelled according to a probability and statistical context:
在统计数据中,就是分布的数据值。 在此,x轴是我们数据的值,而y轴是这些值中每个值的计数。 这是正态分布的同一张图片,但根据概率和统计上下文进行了标记:
In a probability context, the high point in a normal distribution represents the event with the highest probability of occurring. As you get farther away from this event on either side, the probability drops rapidly, forming that familiar bell-shape. The high point in a statistical context actually represents the mean. As in probability, as you get farther from the mean, you rapidly drop off in frequency. That is to say, extremely high and low deviations from the mean are present but exceedingly rare.
在概率上下文中,正态分布中的最高点表示发生概率最高的事件。 随着您从任一端离此事件越来越远,几率Swift下降,形成了熟悉的钟形。 统计上下文中的最高点实际上代表平均值。 正如概率一样,当您远离均值时,频率会Swift下降。 也就是说,存在与平均值的极高和极低的偏差,但极为罕见。
If you suspect there is another relationship between probability and statistics through the normal distribution, then you are correct in thinking so! We will explore this important relationship later in the article, so hold tight.
如果您怀疑通过正态分布的概率与统计量之间存在其他关系,那么您是正确的! 我们将在本文后面探讨这种重要的关系,因此请紧紧抓住。
Since we’ll be using the distribution of scores to compare different wines, we’ll do some set up to capture some wines that we’re interested in. We’ll bring in the wine data and then separate out the scores of some wines of interest to us.
由于我们将使用分数分布来比较不同的葡萄酒,因此我们将进行一些设置以捕获我们感兴趣的一些葡萄酒。我们将引入葡萄酒数据,然后分离出一些葡萄酒的分数对我们感兴趣。
To bring back in the data, we need the following code:
要带回数据,我们需要以下代码:
The data is shown below in tabular form. We need the points column, so we’ll extract this into its own list. We’ve heard from one wine expert that the Hungarian Tokaji wines are excellent, while a friend has suggested that we start with the Italian Lambrusco. We have the data to compare these wines!
数据以表格形式显示在下面。 我们需要points列,因此我们将其提取到自己的列表中。 我们从一位葡萄酒专家那里听说匈牙利的Tokaji葡萄酒非常出色,而一位朋友则建议我们从意大利Lambrusco开始。 我们有数据可以比较这些葡萄酒!
If you don’t remember what the data looks like, here’s a quick table to reference and get reacquainted.
如果您不记得数据是什么样子,这里有个快速的表格供您参考并重新认识。
| index | 指数 | country | 国家 | description | 描述 | designation | 指定 | points | 点数 | price | 价钱 | province | 省 | region_1 | region_1 | region_2 | region_2 | variety | 品种 | winery | 酒厂 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | US | 我们 | “This tremendous 100%…” | “这真是百分百……” | Martha’s Vineyard | 玛莎葡萄园岛 | 96 | 96 | 235 | 235 | California | 加利福尼亚州 | Napa Valley | 纳帕谷 | Napa | 纳帕 | Cabernet Sauvignon | 赤霞珠 | Heitz | 海兹 |
| 1 | 1个 | Spain | 西班牙 | “Ripe aromas of fig… | “无花果的成熟香气…… | Carodorum Selecci Especial Reserva | Carodorum Selecci特别储备 | 96 | 96 | 110 | 110 | Northern Spain | 西班牙北部 | Toro | 托罗 | Tinta de Toro | Tinta de Toro | Bodega Carmen Rodriguez | Bodega卡门·罗德里格斯(Bodega Carmen Rodriguez) | ||
| 2 | 2 | US | 我们 | “Mac Watson honors… | “ Mac Watson荣幸…… | Special Selected Late Harvest | 特别精选晚收 | 96 | 96 | 90 | 90 | California | 加利福尼亚州 | Knights Valley | 骑士谷 | Sonoma | 索诺玛 | Sauvignon Blanc | 长相思 | Macauley | 麦考利 |
| 3 | 3 | US | 我们 | “This spent 20 months… | “这花了20个月…… | Reserve | 保留 | 96 | 96 | 65 | 65 | Oregon | 俄勒冈州 | Willamette Valley | 威拉米特山谷 | Willamette Valley | 威拉米特山谷 | Pinot Noir | 黑比诺 | Ponzi | 庞兹 |
| 4 | 4 | France | 法国 | “This is the top wine… | “这是顶级葡萄酒…… | La Brelade | 拉布雷拉德 | 95 | 95 | 66 | 66 | Provence | 普罗旺斯 | Bandol | 邦多 | Provence red blend | 普罗旺斯红色混合 | Domaine de la Begude | 贝古德酒庄 |
# Extract the Tokaji scores tokaji = [] non_tokaji = [] for wine in wines: if points != '': points = wine[4] if wine[9] == "Tokaji": tokaji.append(float(points)) else: non_tokaji.append(points) # Extract the Lambrusco scores lambrusco = [] non_lambrusco = [] for wine in wines: if points != '': points = wine[4] if wine[9] == "Lambrusco": lambrusco.append(float(points)) else: non_lambrusco.append(float(points))# Extract the Tokaji scores tokaji = [] non_tokaji = [] for wine in wines: if points != '': points = wine[4] if wine[9] == "Tokaji": tokaji.append(float(points)) else: non_tokaji.append(points) # Extract the Lambrusco scores lambrusco = [] non_lambrusco = [] for wine in wines: if points != '': points = wine[4] if wine[9] == "Lambrusco": lambrusco.append(float(points)) else: non_lambrusco.append(float(points))
If we visualize each group of scores as normal distributions, we can immediately tell if two distributions are different based on where they are. But we will quickly run into problems with this approach, as shown below. We assume the scores will be normally distributed since we have a ton of data. While that assumption is okay here, we’ll discuss later when it may actually be dangerous to do so.
如果我们将每组分数可视化为正态分布,则可以根据它们的位置立即判断出两个分布是否不同。 但是我们将很快遇到这种方法的问题,如下所示。 由于我们拥有大量数据,因此我们假设得分将呈正态分布。 尽管这里的假设是可以的,但我们稍后将讨论这样做的实际风险。
When the two score distributions overlap too much, it’s probably better to assume thy actually come from the same distribution and aren’t different. On the other extreme with no overlap, it’s safe to assume that the distributions aren’t the same. Our trouble lay in the case of some overlap. Given that the extreme highs of one distribution may intersect with the extreme lows of another, how can we say if the groups are different?
当两个得分分布重叠太多时,最好假设您实际上来自相同的分布并且没有不同。 在另一个没有重叠的极端情况下,可以安全地假设分布不相同。 我们的麻烦在于某些重叠。 鉴于一种分布的极高点可能与另一种分布的极低点相交,我们如何说这些组是否不同?
Here, we must again call upon the normal distribution to give us an answer and a bridge between statistics and probability.
在这里,我们必须再次呼吁正态分布给我们一个答案,并为统计和概率之间架起一座桥梁。
重温正常 (Revisiting the normal)
The normal distribution is significant to probability and statistics thanks to two factors: the Central Limit Theorem and the Three Sigma Rule.
由于两个因素,正态分布对概率和统计意义重大: 中心极限定理和三西格玛规则 。
中心极限定理 (Central Limit Theorem)
In the previous section, we demonstrated that if we repeated our 10-toss trials many, many times, the average heads-count of all of these trials will approach the 50% we expect from an ideal coin. With more trials, the closer the average of these trials approach the true probability, even if the individual trials themselvesare imperfect. This idea is a key tenet of the Central Limit Theorem.
在上一节中,我们证明了如果我们多次重复进行10次抛掷试验,所有这些试验的平均总人数将接近理想硬币预期的50%。 通过更多的试验,即使单个试验本身并不完美,这些试验的平均值也越接近真实概率。 这个想法是中心极限定理的关键原则。
In our coin-tossing example, a single trial of 10 throws produces a single estimate of what probability suggests should happen (5 heads). We call it an estimate because we know that it won’t be perfect (i.e. we won’t get 5 heads everytime). If we make many estimates, the Central Limit Theorem dictates that the distribution of these estimates will look like a normal distribution. The zenith of this distribution will line up with the true value that the estimates should take on. In statistics, the peak of the normal distribution lines up with the mean, and that’s exactly what we observed. Thus, given multiple “trials” as our data, the Central Limit Theorem suggests that we can hone in on the theoretical ideal given by probability, even when we don’t know the true probability.
在掷硬币的示例中,一次尝试10次投掷就产生了对应该发生的可能性(5头)的单一估计。 我们称其为估算值是因为我们知道它不是完美的(即,我们每次不会得到5个头)。 如果我们做出许多估计,则中心极限定理指示这些估计的分布看起来像正态分布。 此分布的顶点将与估算值应采用的真实值一致。 在统计中,正态分布的峰值与均值一致,这正是我们观察到的。 因此,以多个“试验”作为我们的数据,中心极限定理表明,即使我们不知道真实的概率,我们也可以坚持概率给出的理论理想。
Central Limit Theorem lets us know that the average of many trials means will approach the true mean, the Three Sigma Rule will tell us how much the data will be spread out around this mean.
中心极限定理让我们知道许多试验均值的平均值将接近真实均值,三西格玛规则将告诉我们围绕该均值分布的数据量。
三西格玛规则 (Three Sigma Rule)
The Three Sigma rule, also known as the empirical rule or 68-95-99.7 rule, is an expression of how many of our observations fall within a certain distance of the mean. Remember that the standard deviation (a.k.a. “sigma”) is the average distance an observation in the data set is from the mean.
三西格玛规则(也称为经验规则或68-95-99.7规则)表达了我们有多少观测值落在均值的一定距离内。 请记住,标准差(也称为“ sigma”)是数据集中观察值与平均值之间的平均距离。
The Three Sigma rule dictates that given a normal distribution, 68% of your observations will fall between one standard deviation of the mean. 95% will fall within two, and 99.7% will fall within three. A lot of complicated math goes into the derivation of these values, and as such, is out of the scope of this article. The key takeaway is to know that the Three Sigma Rule enables us to know how much data is contained under different intervals of a normal distribution. The picture below is a great summary of what the Three Sigma Rule represents.
三西格玛(3 Sigma)规则规定, 在正态分布的情况下 ,您的观测值的68%将落在平均值的一个标准偏差之间。 95%将落在两个范围内,而99.7%将落在三个范围内。 这些值的推导涉及很多复杂的数学运算,因此不在本文讨论范围之内。 关键要点在于,三西格玛规则使我们能够知道正态分布的不同间隔下包含多少数据。 下图是“三个西格玛规则”代表的摘要。
We’ll connect these concepts back to our wine data. As a sommelier, we’d like to know with high confidence that Chardonnay and Pinot Noir are more popular than the average wine. We have many thousands of wine reviews, so by Central Limit Theorem, the average score of these reviews should line up with a so-called “true” representation of the wine’s quality (as judged by the reviewer).
我们将把这些概念与我们的葡萄酒数据联系起来。 作为一名侍酒师,我们想非常有信心地知道霞多丽和黑比诺比普通葡萄酒更受欢迎。 我们有成千上万的葡萄酒评论,因此根据中央极限定理,这些评论的平均分数应与葡萄酒质量的所谓“真实”表示一致(由评论者判断)。
Although the Three Sigma rule is a statement of how much of your data falls within known values, it is also a statement of the rarity of extreme values. Any value that is more than three standard deviations away from the mean should be treated with caution or care. By taking advantage of the Three Sigma Rule and the Z-score, we’ll finally be able to prescribe a value to how likely Chardonnay and Pinot Noir are different from the average wine.
尽管“三西格码”规则说明了多少数据属于已知值,但也说明了极值的稀有性。 与平均值相差超过三个标准偏差的任何值都应谨慎对待。 通过利用三西格玛规则和Z分数 ,我们终于可以为霞多丽和黑比诺与普通葡萄酒的差异开出一个值。
Z分数 (Z-score)
The Z-score is a simple calculation that answers the question, “Given a data point, how many standard deviations is it away from the mean?” The equation below is the Z-score equation.
Z分数是一个简单的计算,它回答了以下问题:“给定一个数据点,它与平均值之间有多少标准偏差?” 下面的方程式是Z分数方程式。
By itself, the Z-score doesn’t provide much information to you. It gains the most value when compared against a Z-table, which tabulates the cumulative probability of a standard normal distribution up until a given Z-score. A standard normal is a normal distribution with a mean of 0 and a standard deviation of 1. The Z-score lets us reference this the Z-table even if our normal distribution is not standard.
就其本身而言,Z评分不会为您提供太多信息。 与Z表比较时,它获得的价值最高,该表列出了直到给定Z分数之前标准正态分布的累积概率 。 标准正态分布是平均值为0,标准偏差为1的正态分布。即使我们的正态分布不是标准分布,Z分数也可以让我们参考Z表。
The cumulative probability is the sum of the probabilities of all values occurring, up until a given point. An easy example is the mean itself. The mean is the exact middle of the normal distribution, so we know that the sum of all probabilites of getting values from the left side up until the mean is 50%. The values from the Three Sigma Rule actually come up if you try to calculate the cumulative probability between standard deviations. The picture below provides a visualization of the cumulative probability.
累积概率是直至给定点出现的所有值的概率之和。 一个简单的例子就是平均值。 平均值是正态分布的精确中间值,因此我们知道从左侧一直到平均值获得值的所有概率之和为50%。 如果您尝试计算标准偏差之间的累积概率,则实际上会出现“三西格玛规则”中的值。 下图提供了累积概率的可视化。
We know that the sum of all probabilities must equal 100%, so we can use the Z-table to calculate probabilities on both sides of the Z-score under the normal distribution.
我们知道所有概率之和必须等于100%,因此我们可以使用Z表在正态分布下计算Z分数两侧的概率。
This calculation of probability of being past a certain Z-score is useful to us. It lets us ask go from “how far is a value from the mean” to “how likely is a value this far from the mean to be from the same group of observations?” Thus, the probability derived from the Z-score and Z-table will answer our wine based questions.
这种计算超过某个Z分数的概率对我们很有用。 它让我们问:从“平均值离平均值有多远”到“距平均值有这么远的值来自同一组观察值的可能性有多大?” 因此,从Z分数和Z表得出的概率将回答我们基于葡萄酒的问题。
This doesn’t look good for our friend’s recommendation! For the purpose of this article, we’ll treat both the Tokaji and Lambrusco scores as normally distributed. Thus, the average score of each wine will represent their “true” score in terms of quality. We will calculate the Z-score and see how far away the Tokaji average is from the Lambrusco.
这对我们朋友的推荐来说并不好! 出于本文的目的,我们将Tokaji和Lambrusco分数均视为正态分布。 因此,每种葡萄酒的平均分数将代表其质量的“真实”分数。 我们将计算Z分数,并查看Tokaji平均值与Lambrusco的距离。
z = (tokaji_avg - lambrusco_avg) / lambrusco_std >>> 4.0113309781438229 # We'll bring in scipy to do the calculation of probability from the Z-table import scipy.stats as st st.norm.cdf(z) >>> 0.99996981130231266 # We need the probability from the right side, so we'll flip it! 1 - st.norm.cdf(z) >>> 3.0188697687338895e-05z = (tokaji_avg - lambrusco_avg) / lambrusco_std >>> 4.0113309781438229 # We'll bring in scipy to do the calculation of probability from the Z-table import scipy.stats as st st.norm.cdf(z) >>> 0.99996981130231266 # We need the probability from the right side, so we'll flip it! 1 - st.norm.cdf(z) >>> 3.0188697687338895e-05
The answer is quite small, but what exactly does it mean? The infinitesimal smallness of this probability requires some careful interpretation.
答案很小,但是究竟是什么意思呢? 这种可能性的无穷小需要一些仔细的解释。
Let’s say that we believed that there was no difference between our friend’s Lambrusco and the wine expert’s Tokaji. That is to say, we believe that the quality of the Lambrusco and the Tokaji to be about the same. Likewise, due to individual differences between wines, there will be some spread of the scores of these wines. This will produce normally distured scores if we make a histogram of the Tokaji and Lambrusco wines, thanks to Central Limit Theorem.
假设我们相信朋友的Lambrusco和葡萄酒专家的Tokaji之间没有区别 。 也就是说,我们认为Lambrusco和Tokaji的质量大致相同。 同样,由于葡萄酒之间的个体差异,这些葡萄酒的分数也会有所不同。 如果通过中央极限定理对托卡吉和拉姆布鲁斯科葡萄酒进行直方图,这将产生通常偏离的分数 。
Now, we have some data that allows us to calculate the mean and standard deviation of both wines in question. These values allow us to actually test our belief that Lambrusco and Tokaji were of similar quality. We used the Lambrusco wine scores as a base and compared the Tokaji average, but we could have easily done it the other way around. The only difference would be a negative Z-score.
现在,我们有了一些数据,可以计算出所讨论的两种葡萄酒的平均值和标准偏差。 这些值使我们可以实际检验我们对Lambrusco和Tokaji具有相似质量的看法。 我们以Lambrusco的葡萄酒得分为基础,并比较了Tokaji的平均值,但反之则可以轻松实现。 唯一的不同是Z得分为负。
The Z-score was 4.01! Remember that the Three Sigma Rule tells us that 99.7% of the data should fall within 3 standard deviations, assuming that Tokaji and Lambrusco were similar. The probability of a score average as extreme as Tokaji’s in a world where Lambrusco and Tokaji wines are assumed to be the same is very, very small. So small that we are forced to consider the converse: Tokaji wines are different from Lambrusco wines and will produce a different score distribution.
Z分数是4.01! 请记住,“三西格玛规则”告诉我们,假设Tokaji和Lambrusco相似,则99.7%的数据应在3个标准差之内。 在一个假定Lambrusco和Tokaji葡萄酒相同的世界中,得分平均值与Tokaji一样极端的可能性非常小。 太小了,我们不得不考虑相反的情况:托卡吉(Tokaji)葡萄酒不同于兰布鲁斯科(Lambrusco)葡萄酒,并且会产生不同的分数分布。
We’ve chosen our wording here carefully: I took care not to say, “Tokaji wines are better than Lambrusco.” They are highly probable to be. This is because we calculated a probability which, though microscopically small, is not zero. In order to be precise, we can say that Lambrusco and Tokaji wines are definitively not from the same score distribution, but we cannot say that one is better or worse than the other.
我们在这里精心选择了措辞:我注意不要说“托卡吉葡萄酒比Lambrusco好。” 他们很有可能成为。 这是因为我们计算出的概率虽然在微观上很小,但不为零。 确切地说,我们可以说拉姆布鲁斯科和托卡吉葡萄酒肯定不是来自相同的分数分布,但是我们不能说一个比另一个更好或更差。
This type of reasoning is within the domain of inferential statistics, and this article only seeks to give you a brief introduction into the rationale behind it. We covered a lot of concepts in this article, so if you found yourself getting lost, go back and take it slow. Having this framework of thinking is immensely powerful, but easy to misuse and misunderstand.
这种类型的推理属于推论统计的范畴,本文仅旨在向您简要介绍其背后的原理。 我们在本文中介绍了很多概念,因此,如果您发现自己迷路了,请回过头慢慢来。 拥有这种思维框架非常强大,但容易被误用和误解。
结论 (Conclusion)
We started with descriptive statistics and then connected them to probability. From probability, we developed a way to quantatively show if two groups come from the same distribution. In this case, we compared two wine recommendations and found that they most likely do not come from the same score distribution. In other words, one wine type is most likely better than the other one.
我们从描述性统计开始,然后将它们与概率联系起来。 根据概率,我们开发了一种方法来定量显示两组是否来自同一分布。 在这种情况下,我们比较了两种葡萄酒建议,发现它们很可能并非来自相同的分数分布。 换句话说,一种葡萄酒最有可能比另一种更好。
Statistics doesn’t have to be a field relegated to just statisticians. As a data scientist, having an intuitive understanding on common statistical measures represent will give you an edge on developing your own theories and the ability to subsequently test these theories. We barely scratched the surface of inferential statistics here, but the same general ideas here will help guide your intuition in your statistical journey. Our article discussed the advantages of the normal distribution, but statisticians have also developed techniques to adjust for distributions that aren’t normal.
统计信息不必仅限于统计学家。 作为数据科学家,对常见的统计量表示有一个直观的了解将使您在开发自己的理论方面具有优势,并且可以随后测试这些理论。 我们在这里几乎没有涉及推论统计的内容,但是这里的相同一般思想将有助于指导您进行统计之旅。 我们的文章讨论了正态分布的优势,但统计学家还开发了调整非正态分布的技术。
进一步阅读 (Further Reading)
This article centered around the normal distribution and its connection to statistics and probability. If you’re interested in reading about other related distributions or learning more about inferential statistics, please refer to the resources below.
本文围绕正态分布及其与统计数据和概率的关系进行讨论。 如果您有兴趣阅读其他相关分布或对推论统计信息有更多了解,请参考以下资源。
- Student’s T-distribution: when we only have a few data points
- A deeper dive into hypothesis testing and inferential statistics
- An in-depth dive into statistics with Python
- 学生的T分布:当我们只有几个数据点时
- 深入探讨假设检验和推论统计
- 使用Python深入了解统计信息
翻译自: https://www.pybloggers.com/2018/07/basic-statistics-in-python-probability/
python统计分布和概率