2019暑假牛客多校第五场B.generator 1(十进制矩阵快速幂)

B.generator 1

传送门

You are given four positive integers $x_0,x_1,a,b$. And you know $x_i=a\cdot x_{i-1}+b\cdot x_{i-2}$ for all $i\ge 2$.

Given two positive integers n, and MOD, please calculate $x_n$ modulo MOD.

Does the problem look simple? Surprise! The value of n may have many many digits!
输入描述:
The input contains two lines.
The first line contains four integers $x_0,x_1,a,b$,a,b ($1\le x_0,x_1,a,b\le 10^9$ ).
The second line contains two integers n, MOD ($41\le n<10^{(10^6)}$, $10^9<MOD\le 2\times 10^9$, n has no leading zero).
输出描述:
Print one integer representing the answer.
示例1
输入
1 1 1 1
10 1000000001
输出
89
说明
The resulting sequence x is Fibonacci sequence. The 11-th item is 89.
示例2
输入
1315 521 20185 5452831
9999999999999999999999999999999999999 1000000007
输出
914730061
题意
给你$x_0$、$x_1$、a、b、b、mod，根据$x_i=a\ast x_{i-1}+b\ast x_{i-2}$求出$x_n$

思路
一般看到这种题就会想到矩阵快速幂，但是这次的n太大了，所以要用十进制倍增来算,（第一种做法）。同时还可以用二进制快速幂优化它（第二种做法）。

• 矩阵快速幂的通项式
  
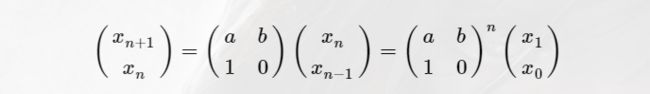
• 用十进制

设$\left(\genfrac{}{}{0ex}{}{ab}{10}\right)$为res
则可得$ans=re{s}^{n[i]{-}^{\prime }{0}^{\prime }}$（n[i]用字符串储存n）
我们再设res =$re{s}^{10(i-1)}$;
就是分解n为每一位，再去相乘。
如
$re{s}^{298}=re{s}^{1\ast 8}\ast re{s}^{10\ast 9}\ast re{s}^{100\ast 2}$
计算每一位即可。
所以最后就是
len(n)→1
  ans=ans*cul(res,n[i]-‘0’);
  res=pow(res,10);

ac代码(1512ms):

#include 
using namespace std;
typedef long long ll;
const int Maxn=1e6+10;
struct node{
     
    ll mat[2][2];
};

ll x0,x1,a,b,mod;
node ans,O,tmp,z;
char n[Maxn];
node cul(node x,node y){
         //矩阵乘法
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++){
     
            z.mat[i][j]=0;
            for(int k=0;k<2;k++)
                z.mat[i][j]=(z.mat[i][j]+x.mat[i][k]*y.mat[k][j])%mod;
    }
    return z;
}

int main(){
     
    int op;
    scanf("%lld %lld %lld %lld %s %lld",&x0,&x1,&a,&b,n,&mod);
    int len=strlen(n);
    ans.mat[0][0]=ans.mat[1][1]=1;
    tmp.mat[0][0]=a;
    tmp.mat[0][1]=b;
    tmp.mat[1][0]=1;
    for(int i=len-1;i>=0;i--){
     
        op=n[i]-'0';
        for(int j=0;j<op;j++) ans=cul(ans,tmp); //矩阵乘法得res^op
        O.mat[0][0]=O.mat[1][1]=1;  //初等矩阵
        O.mat[0][1]=O.mat[1][0]=0;
        for(int j=0;j<10;j++) O=cul(O,tmp); //直接跑十遍，求res^10n
        tmp=O;
    }
    printf("%lld\n",(x1*ans.mat[1][0]+x0*ans.mat[1][1])%mod);
    return 0;
}

另一种写法（1800ms）：

#include
#define mes(a, b) memset(a, b, sizeof a)
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
ll mod;
char n[maxn];

struct Mat{
     
    ll mat[4][4];
    Mat(){
     
        mes(mat,0);
    }
    void init(){
     
        for(int i=1;i<=2;i++)
            mat[i][i]=1;
    }

    Mat operator*(const Mat &a)const{
       //矩阵乘法
        Mat ans;
        for(int i=1;i<=2;i++){
     
            for(int j=1;j<=2;j++){
     
                for(int k=1;k<=2;k++){
     
                    ans.mat[i][j]+=mat[i][k]*a.mat[k][j]%mod;
                    ans.mat[i][j]%=mod;
                }
            }
        }
        return ans;
    }
};

Mat pow(Mat a, ll b){
      //矩阵快速幂
    Mat ans;
    ans.init();
    while(b){
     
        if(b&1)
            ans=ans*a;
        a=a*a;
        b>>=1;
    }
    return ans;
}

int main(){
     
    ll a,b,x1,x0;
    scanf("%lld%lld%lld%lld",&x0,&x1,&a,&b);
    scanf("%s%lld",n,&mod);
    int len=strlen(n);
    Mat ans; ans.init();
    Mat res;
    res.mat[1][1]=a;res.mat[1][2]=b;
    res.mat[2][1]=1;
    for(int i=len-1;i>=0;i--){
     
        ans=ans*pow(res,n[i]-'0'); 
        res=pow(res,10ll); //用快速幂跑
    }
    Mat f;
    f.mat[1][1]=x1;
    f.mat[2][1]=x0;
    f=ans*f;
    printf("%lld\n",f.mat[2][1]);
    return 0;
}