牛客算法进阶(一)
一、窗口应用
生成窗口最大值数组
给出一个整形数组,例如arr = {5,4,3,5,6,7,6},窗口大小为w=3,窗口每次向右移动一位,输出每个窗口中最大值组成的数组。
[5,4,3,]5,6,7,6 窗口最大值为5
5,[4,3,5,]6,7,6 窗口最大值为5
5,4,[3,5,6,]7,6 窗口最大值为6
5,4,3,[5,6,7,]6 窗口最大值为7
5,4,3,5,[6,7,6] 窗口最大值为7
则输出的数组为{5,5,6,7,7};
思路:
双端队列,将arr中的元素加入res该队列中,若该队列的队尾元素小于等于要加入的元素,则不断的弹出,直到队尾元素大于该元素或者队列为空。此时将该元素的序号加入队列中。同时当 i-w == 队头的序号,则将队头元素弹出。
代码:
#include
#include
#include
using namespace std;
vector getMAXWindow(vectorvec, int w) {
int len = vec.size();
deque q;
vector res;
if (len <= 0 || w < 1 || len < w) {
return res;
}
for (int i = 0; i < len; i++) {
//往双端队列中加入元素
while (!q.empty() && vec[q.back()] <= vec[i]) {
q.pop_back();
}
q.push_back(i);
//判断当前双端队列的头节点是否过期
if (q.front() == i - w)
q.pop_front();
//当i的值超过w-1后,每次都需要收集当前的最大值
if (i >= w - 1)
res.push_back(vec[q.front()]);
}
return res;
}
int main(void) {
vector vec = { 4,3,5,4,3,3,6,7 };
int w = 3; //窗口大小
vector res = getMAXWindow(vec, w);
for (auto i : res)
cout << i << " ";
system("pause");
return 0;
}
最大值减去最小值小于或等于num的子数组的数量
给定数组 arr 和整数 num,共返回多少个字数组满足如下情况:
max(arr[i...j]) - min(arr[i...j]) <= num
max(arr[i...j]) 表示字数组 arr[i...j] 中的最大值,min(arr[i...j]) 表示子数组 arr[i...j] 中的最小值。
思路:
1.子数组的数量一共为n+(n-1)+...+2+1
2.若 arr[i...j] 满足条件,那么其子数组也会满足条件;
3.若 arr[i...j] 不满组条件,那么包含arr[i...j]的数组都不满足条件;
代码:
#include
#include
using namespace std;
int getNum(int arr[], int len, int num)
{
if (NULL == arr || 0 >= len)
return 0;
deque qmin; //qmLn的第一个数据总是当前数组中最小的数据的位置
deque qmax; //qmax的第一个数据总是当前数组中最大的数据的位置
int L = 0, R = 0, res = 0;
//固定左边,窗口右边一直扩大找符合条件的
while (L < len)
{
while (R < len)
{
while (!qmin.empty() && arr[qmin.front()] >= arr[R])
qmin.pop_back();
qmin.push_back(R);
while (!qmax.empty() && arr[qmax.front() <= arr[R]])
qmax.pop_back();
qmax.push_back(R);
//找到了第一个不符合条件的,后面的R都不符合,
//因为后面的子数组中都包含当前这个不符合的R
if (arr[qmax.front()] - arr[qmin.front()] > num)
break;
R++;
}
res += R - L; //记录当前序列中满足要求的字数组数量
if (qmin.front() == L)
qmin.pop_front();
if (qmax.front() == L)
qmax.pop_front();
L++;//窗口左边界向右移动
}
return res;
}
int main(void)
{
int a[] = { 3,2,5,1,4,7,8,6 };
cout << "The number of sub arrays to meet the requLrements Ls: " << getNum(a, 8, 4) << endl;
system("pause");
return 0;
} 子数组为固定值的最长长度
给定一个数组arr,全是正数;一个整数aim,求累加和等于aim的,最长子数组,要求额外空间复杂度O(1),时间复杂度O(N)
思路:
构建一个窗口,因为所有的元素均为正整数,所以,当前窗口的总和只要小于给定值,窗口右边界就向右移动;当前窗口如果等于给定值,那么就说明找到一个子数组,进行长度的对比,然后窗口左边界向右移动,继续进行比较;当前窗口如果大于给定值,说明元素太多了,需要将窗口左边界向右移动。
代码:
#include
#include
#include
using namespace std;
int getMaxLength(vector &arr, int k)
{
if (arr.size() < 1 || k <= 0)
return 0;
int L = 0;//窗口左边界
int R = 0;//窗口右边界
int sum = arr[0];
int maxLen = 0;
while (R < arr.size())//只要窗口右边界还存在就循环
{
if (sum == k)
{
maxLen = max(maxLen, R - L + 1);
sum -= arr[L++];//窗口左边界向右移动
}
else if (sum < k)
{
R++;//窗口右边界向右移动
if (R == arr.size())
break;
sum += arr[R];
}
else
sum -= arr[L++];//当前总和大于k,窗口左边界向右移动
}
return maxLen;
}
int main(void)
{
system("pause");
return 0;
}
二、单调栈的应用
定义:
从栈底元素到栈顶元素呈单调递增或单调递减,栈内序列满足单调性的栈;
原理:
(1)当新元素在单调性上优于栈顶时(单增栈新元素比栈顶大,单减栈新元素比栈顶小),压栈,栈深+1;
(2)当新元素在单调性与栈顶相同(新元素于栈顶相同)或劣于栈顶时(单增栈新元素比栈顶小,单减栈新元素比栈顶大),弹栈,栈深-1
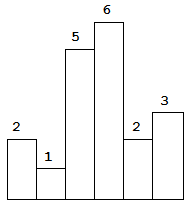
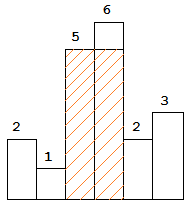
直方图中最大的矩形
思路:
一旦遇到比自己小的元素,就开始结算以当前元素为高的矩形面积。
#include
#include
#include
#include
using namespace std;
class Solution {
public:
int largestRectangleArea(vector& heights)
{
int res = 0;
stack st;
/*
巧妙的地方,故意多加一位0,保证栈中的元素都会被计算,
这样就不用再去判断栈中是否还有没出来的元素了
*/
heights.push_back(0);
for (int i = 0; i < heights.size(); ++i)
{
while (!st.empty() && heights[st.top()] >= heights[i])
{
int cur = st.top(); st.pop();
//注意:单调栈中的最后一个元素的宽度为整个heights的长度
res = max(res, heights[cur] * (st.empty() ? i : (i - st.top() - 1)));
}
//当前节点肯定会被加入单调栈中,之前的元素如果比当前节点的值
//要大,进行弹出结算
st.push(i);
}
return res;
}
}; 最大矩形
其实就是上面的直方图的最大矩形的变形。
这道题的二维矩阵每一层向上都可以看做一个直方图,输入矩阵有多少行,就可以形成多少个直方图,对每个直方图都调用上一题中的方法,就可以得到最大的矩形面积。那么这道题唯一要做的就是将每一层构成直方图,由于题目限定了输入矩阵的字符只有 '0' 和 '1' 两种,所以处理起来也相对简单。方法是,对于每一个点,如果是‘0’,则赋0,如果是 ‘1’,就赋 之前的height值加上1。
具体来说,就是一行一行的看,把第一行当作一个矩形计算,求最大值;然后在第一行的基础上加入第二行,求这两行构成的矩形求最大值,和之前做max,以此类推,直到所有的行都计算完。
#include
#include
#include
#include
using namespace std;
/*
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6
*/
//该设计是单调栈中的小端栈,也就是从栈底到栈顶是从小到大
int maximalRectangle(vector>& matrix)
{
if (matrix.empty() || matrix[0].empty())
return 0;
int result = 0;
int m = matrix.size(), n = matrix[0].size();
/*
巧妙的地方,故意多加一位0,保证栈中的元素都会被计算,
这样就不用再去判断栈中是否还有没出来的元素了
*/
vector height(n + 1, 0);
for (int i = 0; i < m; ++i)
{
stack s;
for (int j = 0; j < n + 1; ++j)
{
//height中保存的是高度
if (j < n)
height[j] = matrix[i][j] == '1' ? height[j] + 1 : 0;
while (!s.empty() && height[s.top()] >= height[j])
{
int cur = s.top();
s.pop();
result = max(result, height[cur] * (s.empty() ? j : (j - s.top() - 1)));
}
s.push(j);
}
}
return result;
} 山峰对数量
https://blog.csdn.net/zxzxzx0119/article/details/81662792
三、Morris算法
https://blog.csdn.net/u013575812/article/details/50069991
#include
using namespace std;
typedef int dataType;
struct Node
{
dataType val;
struct Node *left;
struct Node *right;
Node(dataType _val):
val(_val), left(NULL), right(NULL){}
};
// Morris中序遍历 (左 -> 根 -> 右)
void MorrisInOrderTraverse(Node *head)
{
if (head == NULL)
{
return;
}
Node *p1 = head;
Node *p2 = NULL;
while (p1 != NULL)
{
p2 = p1->left;
if (p2 != NULL)
{
while(p2->right != NULL && p2->right != p1)
{
p2 = p2->right;
}
if (p2->right == NULL)
{
p2->right = p1; // 空闲指针
p1 = p1->left;
continue;
}
else
{
p2->right = NULL;
}
}
//对于有左子树的节点,选择第二次遍历到这个节点的时候进行打印,
//如果没有左子树,那总共就遍历过一次,也就无所谓了。
cout<val<<" ";
p1 = p1->right;
}
}
// Morris前序遍历 (根 -> 左 -> 右)
void MorrisPreOrderTraverse(Node *head)
{
if (head == NULL)
{
return;
}
Node *p1 = head;
Node *p2 = NULL;
while (p1 != NULL)
{
p2 = p1->left;
if (p2 != NULL)
{
while(p2->right != NULL && p2->right != p1)
{
p2 = p2->right;
}
if (p2->right == NULL)
{
p2->right = p1; // 空闲指针
cout<val<<" "; // 第一次来到这个节点
p1 = p1->left;
continue;
}
else
{
p2->right = NULL;
}
}
else
{
cout<val<<" ";//选择打印的时机是第一次来到一个节点的时候
}
p1 = p1->right;
}
}
// 逆序右边界
Node* reverseEdge(Node *head)
{
Node *pre = NULL;
Node *next = NULL;
while(head != NULL)
{
next = head->right;
head->right = pre;
pre = head;
head = next;
}
return pre;
}
// 逆序打印左子树右边界
void printEdge(Node *head)
{
Node *lastNode = reverseEdge(head);
Node *cur = lastNode;
while (cur != NULL)
{
cout<val<<" ";
cur = cur->right;
}
reverseEdge(lastNode);
}
// Morris后序遍历 (左 -> 右 -> 根)
void MorrisPostOrderTraverse(Node *head)
{
if (head == NULL)
{
return;
}
Node *p1 = head;
Node *p2 = NULL;
while (p1 != NULL)
{
p2 = p1->left;
if (p2 != NULL)
{
while(p2->right != NULL && p2->right != p1)
{
p2 = p2->right;
}
if (p2->right == NULL)
{
p2->right = p1; // 空闲指针
p1 = p1->left;
continue;
}
else
{
p2->right = NULL;
/*
把打印时机放在第二次来到一个节点的时候,这个第二次指的
是必须能有第二次回到自己的机会,然后逆序打印左子树
的右边界
*/
printEdge(p1->left);
}
}
p1 = p1->right;
}
//在整个函数退出之前,打印整棵树的右边界
printEdge(head);
}
void buildBinTree(Node **head)
{
dataType _val;
cin>>_val;
if (_val == -1)
{
*head = NULL;
}
else
{
*head = (Node*)malloc(sizeof(Node));
(*head)->val = _val;
buildBinTree(&(*head)->left);
buildBinTree(&(*head)->right);
}
}
int main(void)
{
Node *head;
buildBinTree(&head);
cout<<"前序遍历序列为:";
MorrisPreOrderTraverse(head);
cout< 四、部分连续的问题
子数组、子串的问题,也就是部分连续的问题,常见的解题思路是以每个位置结尾进行求解答案
未排序数组中累加和为给定值的最长子数组
给定一个数组arr,和一个整数num,求在arr中,累加和等于num的最长子数组的长度例子:arr = {7,3,2,1,1,7,7,7} num = 7其中有很多的子数组累加和等于7,但是最长的子数组是{3,2,1,1},所以返回其长4
算法流程
1.记录一个全局最大res,记录一个sum表示从0位置一直加到当前位置的累加和,使用一个map来记录前边遍历过程中出现过的累加和。
2.遍历数组,对于当前位置i,首先更新sum,然后看map中有没有sum-k这个键,如果有,则取出这个键对应的值j,表明(i,j]这一小段子序列的和就为k,用这个k去更新我们的res。遍历结束之后res就为我们的最大。如果没有,这把这个位置和sum放入map中。
3.需要特别注意的是首先要把(0,-1)放进map中。比如arr=[5,-1,-1,-1],k=5,如果不放入(0,-1),在考察位置0的时候,其实刚好这个和是满足条件的,但是被忽略了。
算法原理
这里的map记录的是累加和第一次出现某个值的位置。我们在遍历到j的时候,知道sum[j]=0,1,2,,,j的这些元素的累加和,sum[i]为0,1,,,,i这些数的累加和。考察位置j,我们需要找到第一次累加和为sum[j]-k的位置,如果找到了这个位置,那么就有i+1,i+2,...j这些元素的累加和为k,也就求得了以位置j结尾的累加和为k的最长子序列。我们遍历了数组一遍,所有位置结尾的,如果有满足条件的子序列,都求出来了,在这些中的最长的即为所求。
#include
#include
#include
#include
using namespace std;
int maxLength(vector &v, int k)
{
if (v.empty())
return 0;
unordered_map map;
//map::iterator iter;
map.insert (pair(0, -1));
int len = 0;//最长子数组的长度
int sum = 0;//每次都统计新加入一个元素之后的总和
for (int i = 0; i < v.size(); ++i)
{
sum += v[i];
if (map.find(sum - k) != map.end())//find的返回值是迭代器
len = max(i - (map.find(sum - k)->second), len);
if (map.find(sum) == map.end())//如果当前的总和在之前从未出现过,则加入map
map.insert(pair(sum, i));
}
return len;
}
int main(void)
{
vector v = { 7,3,2,1,1,7,7,7 };
int result = maxLength(v, 7);
cout << result << endl;
system("pause");
return 0;
} 还有类似的问题:
1.一个数组中只有0和1,求0和1相等的最长子数组
思路:1还是1,0变为-1,接下来求累加和为0的最长子数组即可。
2.一个整数数组中要么是奇数要么是偶数,请你求奇数和偶数相等的最长子数组。
思路:把奇数变为1,偶数变为-1,接下来求累加和为0的最长子数组。
3.一个数组中含有0、1、2,求含有1的数量和含有2的数量相等的最长子数组。
思路:0还是0,1还是1,将2变为-1,接下来求累加和为0的最长子数组。
子数组的最大异或和
定义数组的异或和的概念:
数组中所有的数异或起来,得到的结果叫做数组的异或和,
比如数组{3,2,1}的异或和是,3^2^1 = 0
给定一个数组arr,你可以任意把arr分成很多不相容的子数组,你的目的是:
分出来的子数组中,异或和为0的子数组最多。
请返回:分出来的子数组中,异或和为0的子数组最多是多少?
思想和上面类似
#include
#include
#include
#include
using namespace std;
int mostEOR(vector &v)
{
int result = 0;//最后的结果
int xor1 = 0;
vector mosts(v.size(), 0);
unordered_map map;
map[0] = -1;//-1代表下标,0代表当前的异或和
for (int i = 0; i < v.size(); ++i)
{
xor1 ^= v[i];//每次都先和之前的异或结果进行异或
//如果之前有异或和为xor1,说明当时的下标往后一个位置到现在的i异或和正好为0
if (map.find(xor1) != map.end())
{
int pre = map.find(xor1)->second;
mosts[i] = pre == -1 ? 1 : (mosts[pre] + 1);
}
if (i > 0)
mosts[i] = max(mosts[i - 1], mosts[i]);
map[xor1] = i;
result = max(result, mosts[i]);
}
return result;
}
int main(void)
{
vector v = {100,1,2,3 };
int result = mostEOR(v);
cout << result << endl;
system("pause");
return 0;
}