本文首发于微信公众号【WriteOnRead】,欢迎关注。
1. 概述
前面数据结构与算法笔记对红黑树进行了分析,而 TreeMap 内部就是基于红黑树实现的。示意图:
它的查找、插入、删除操作的时间复杂度均为 O(logn)。
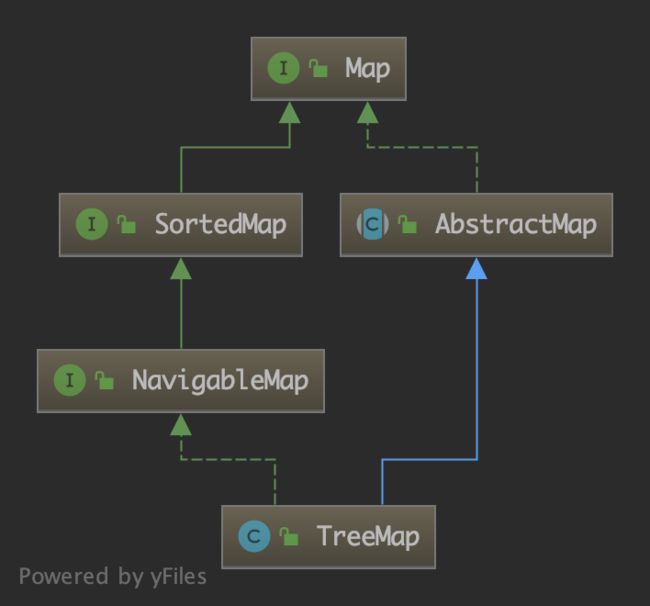
TreeMap 类的继承结构如下:
类签名:
public class TreeMap
extends AbstractMap
implements NavigableMap, Cloneable, java.io.Serializable TreeMap 实现了 Map 接口,其内部数据格式是“键-值对”的形式(Entry),排列顺序是按照键的顺序进行的。
2. 代码分析
2.1 成员变量
/**
* The comparator used to maintain order in this tree map, or
* null if it uses the natural ordering of its keys.
*
* TreeMap 内部的比较器,若为空,则为自然顺序
*/
private final Comparator comparator;
// 根节点
private transient Entry root;
/**
* The number of entries in the tree
*/
private transient int size = 0;
/**
* The number of structural modifications to the tree.
*/
private transient int modCount = 0; 2.2 构造器
TreeMap 有四个构造器,分别如下:
/**
* 无参构造器。使用 key 的自然顺序排列(key 要实现 Comparable 接口)
*/
public TreeMap() {
comparator = null;
}
/**
* 使用指定的 Comparator(比较器)构造一个空的 TreeMap
*/
public TreeMap(Comparator comparator) {
this.comparator = comparator;
}
/**
* 使用给定的 Map 构造一个 TreeMap
*/
public TreeMap(Map m) {
comparator = null;
putAll(m);
}
/**
* 使用给定的 SortedMap 构造一个 TreeMap
*(使用 SortedMap 的顺序)
*/
public TreeMap(SortedMap m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
} 2.3 常用方法
- 查找某个 key
// 判断 TreeMap 是否包含某个 key
public boolean containsKey(Object key) {
return getEntry(key) != null;
}
// 查找 TreeMap 中某个 key 对应的 value(若不存在返回 null)
public V get(Object key) {
Entry p = getEntry(key);
return (p==null ? null : p.value);
} 由于这两个方法内部都是通过 getEntry 方法实现,因此放在一起分析,如下:
final Entry getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
Entry p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
} 当 Comparator 不为空时,使用如下方法查找:
/**
* Version of getEntry using comparator. Split off from getEntry
* for performance. (This is not worth doing for most methods,
* that are less dependent on comparator performance, but is
* worthwhile here.)
*/
final Entry getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator cpr = comparator;
if (cpr != null) {
Entry p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
} 可以看到,这两个方法都是二叉查找树的查找过程。
PS: 这里将 Comporator 和 Comparable 两个接口分开进行操作。注释说明是出于性能考虑,虽然大部分方法中不值得这样做,但这里值得。
- 查找某个 value
public boolean containsValue(Object value) {
for (Entry e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
} getFirstEntry() 方法是获取第一个 Entry 节点(中序遍历最左边的节点):
/**
* Returns the first Entry in the TreeMap (according to the TreeMap's
* key-sort function). Returns null if the TreeMap is empty.
*/
final Entry getFirstEntry() {
Entry p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
} 查找某个 Entry 的后继节点:
/**
* Returns the successor of the specified Entry, or null if no such.
*/
static TreeMap.Entry successor(Entry t) {
if (t == null)
return null;
// 若右子树不为空,则后继节点就是右子树的最小节点
else if (t.right != null) {
Entry p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
// 若右子树为空,则向上回溯
Entry p = t.parent;
Entry ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
} 可以看到,这里判断 TreeMap 是否包含某个 value,是按照二叉查找树的中序遍历去比较是否存在与给定 value 相等的值。
lowerEntry / lowerKey: 查找比指定 key 小的最大 Entry / key
public Map.Entry lowerEntry(K key) {
return exportEntry(getLowerEntry(key));
}
public K lowerKey(K key) {
return keyOrNull(getLowerEntry(key));
} /**
* Returns the entry for the greatest key less than the specified key; if
* no such entry exists (i.e., the least key in the Tree is greater than
* the specified key), returns {@code null}.
*/
final Entry getLowerEntry(K key) {
Entry p = root;
while (p != null) {
int cmp = compare(key, p.key);
// 给定的key大于根节点,继续与右子节点比较
if (cmp > 0) {
if (p.right != null)
p = p.right;
else
return p;
} else {
// 左子节点不为空,则为左子节点
if (p.left != null) {
p = p.left;
} else {
// 左子节点为空,向父节点上溯
Entry parent = p.parent;
Entry ch = p;
while (parent != null && ch == parent.left) {
ch = parent;
parent = parent.parent;
}
return parent;
}
}
}
return null;
} higherEntry / higherKey: 查找比指定 key 大的最小 Entry / key
public Map.Entry higherEntry(K key) {
return exportEntry(getHigherEntry(key));
}
public K higherKey(K key) {
return keyOrNull(getHigherEntry(key));
} getHigherEntry 方法与 getLowerEntry 方法实现类似,不同之处在于 left 和 right 相反,这里不再贴代码。
- floorEntry / floorKey
public Map.Entry floorEntry(K key) {
return exportEntry(getFloorEntry(key));
}
public K floorKey(K key) {
return keyOrNull(getFloorEntry(key));
} /**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the greatest key less than the specified
* key; if no such entry exists, returns {@code null}.
*/
final Entry getFloorEntry(K key) {
Entry p = root;
while (p != null) {
int cmp = compare(key, p.key);
if (cmp > 0) {
if (p.right != null)
p = p.right;
else
return p;
} else if (cmp < 0) {
if (p.left != null) {
p = p.left;
} else {
Entry parent = p.parent;
Entry ch = p;
while (parent != null && ch == parent.left) {
ch = parent;
parent = parent.parent;
}
return parent;
}
} else
// 与上述方法的区别
return p;
}
return null;
} 查找指定 key 关联的 Entry;若不存在,返回比该 key 小的最大 key 关联的 Entry;若这也不存在则返回 null。
PS: 该方法与上面的 getLowerEntry 方法仅相差 while 循环内部的一个 else。
- ceilingEntry / ceilKey
public Map.Entry ceilingEntry(K key) {
return exportEntry(getCeilingEntry(key));
}
public K ceilingKey(K key) {
return keyOrNull(getCeilingEntry(key));
} getCeilingEntry 方法与 getFloorEntry 方法实现类似,也是 left 和 right 相反。就像上面 getLowerEntry 和 getHigherEntry 的区别那样,这里不再贴代码。
查找指定 key 关联的 Entry;若不存在,返回比该 key 大的最小 key 关联的 Entry;若这也不存在则返回 null。
还有几个截取 TreeMap 一部分的方法,分别如下:
public NavigableMap headMap(K toKey, boolean inclusive) {
return new AscendingSubMap<>(this,
true, null, true,
false, toKey, inclusive);
}
public NavigableMap tailMap(K fromKey, boolean inclusive) {
return new AscendingSubMap<>(this,
false, fromKey, inclusive,
true, null, true);
}
public NavigableMap subMap(K fromKey, boolean fromInclusive,
K toKey, boolean toInclusive) {
return new AscendingSubMap<>(this,
false, fromKey, fromInclusive,
false, toKey, toInclusive);
} 除此之外,最常用的插入和删除操作还未分析,这两部分比较复杂,因此留到后面单独分析。
3. 小结
- TreeMap 实现了 Map 接口,内部节点类型为 Entry;
- 基于红黑树实现,具有红黑树的特点;
- 有序,根据 Entry 的 key 排序;
- 查找、插入、删除操作的时间复杂度均为 O(logn)。
相关阅读:数据结构与算法笔记(四)
![]()