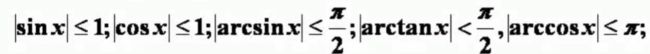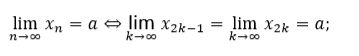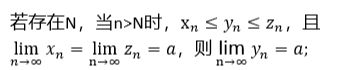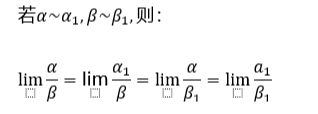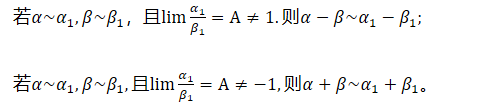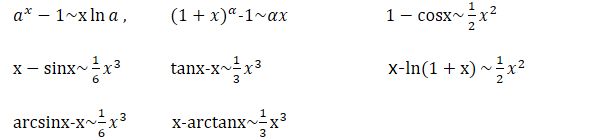同济高等数学第一章之经典错误

1.函数

1.复合函数

复合函数（y=f(u)、u=g(x)）的条件：
f(u)的定义域和g(x)的值域相交不为空。

结论：不是任何两个函数都可以是复合函数。

2.反函数

一个y只能对应唯一确定x，多个x可以对应同一个y。。

结论：

3.初等函数

奇函数的图形关于原点对称，且若f(x)在x=0处有定义，则f(0)=0；
偶函数的图形关于y轴对称。

奇+奇=奇、偶+偶=偶、奇×奇=偶、偶×偶=偶、奇×偶=奇

周期性
1.sinx,cosx周期2π；sin2x,|sinx|周期为π。
2.若f(x)以T为周期，则f(ax+b)以T/|a|为周期（周期必须为正数，所以要加绝对值）。

有界性

2.极限

1.数列的极限

1.定义

数列{Xn}的极限与前有限项无关。

当奇数的极限等于偶数的极限是函数有极限的充分必要条件。

2.数列的有界性：

如果数列{Xn}收敛，那个数列{Xn}一定有界，反之不然。

3.数列的保号性：

1.如果A>0(或A<0)，则存在N>0，当n>N时，Xn>0(或Xn<0)。
2.如果存在N>0,当n>N时，Xn大于等于0(Xn小于等于0), A大于等于0(或A小于等于0)。

保号性之经典错误

2.函数的极限

1.定义

数列和函数中定义域的区别：

当负无穷的极限和正无穷的极限相等，是函数具有极限的充分必要条件。

例题：

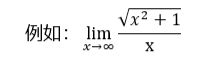
需求出它的到正无穷的极限和负无穷的极限，分别为1和-1，所以函数极限不存在。

求左右边极限之经典错误

2.函数的有界性:

如果f(x)在x0处存在极限，则f(x)在x0处局部有界，反之不然。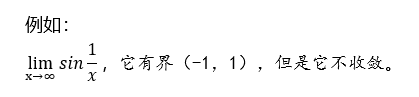

3.函数的保号性以经典错误：

和数列的保号性定理和经典错误类似。

经典错误
例如：用g(x)(极限为A)>f(x)(极限为B)，来推出A>B。
显然是错误的。
可以化为g(x)-f(x)>0，来推出A>B,根据函数的保号性的经典错误第二条(和数列经典错误第二条类似)显然是错误，只能推出A大于等于B。

4.极限值与无穷小之间的关系

3.极限存在准则

1.夹逼准则

2.单调有界准则

单调有界数列必有极限。
单调增、有上界的数列必有极限。
单调减、有下界的数列必有极限。

4.无穷小量

无穷小的性质：
1.有限个无穷小的和仍是无穷小。
2.有限个无穷小的积仍是无穷小。
3.无穷小量与有界量的积仍是无穷小。

5.无穷大量

1.函数的无穷大量的比较

2.数列的无穷大量的比较

3.无穷大量的性质

1.两个无穷大量的积仍然是无穷大量。
2.无穷大量与有界变量之和仍然是无穷大量。

4.无穷大量与无界变量的关系

无穷大量的定义：

无界变量的定义：

无穷变量一定是无界变量，无界变量不一定是无穷变量。例如：1,0,3,0,5,0…
它是无界变量，但是它不是无穷变量。

5.无穷大量与无穷小量的关系

在同一个极限过程中，如果f(x)是一个无穷大，则1/f(x)是无穷小；反之，如果f(x)是无穷小，且f(x)不等于0，则1/f(x)是无穷大量。

3.求极限

1.利用基本极限求极限

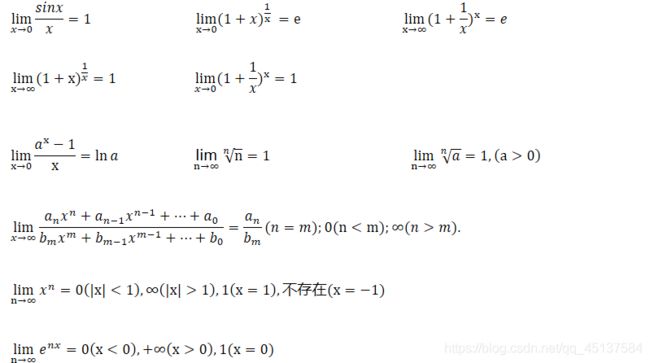
若lim a(x)=0,lim b(x)=无穷,且lim a(x)b(x) =A,则lim(1+a(x))的b(x)次方=e的A次方。

2.利用等级无穷小代换求极限

乘数关系：

加减关系：

常用的等价无穷小：

3.利用有理运算法则求极限

若lim f(x)=A，lim g(x)=B，那么：
lim (f(x)+g(x))=limf(x)+limg(x)=A+B,相减同理可得。
lim (f(x)*g(x))=lim f(x)lim g(x)=AB。
lim (f(x)/g(x))=lim f(x)/lim g(x)=A/B (B≠0）。