题解——二叉树哈夫曼编码的实现
题解——二叉树哈夫曼编码的实现
题目链接:传送门
题面
描述
输入
第一行:采用括号表示法的树字符串
第二行:每个叶子结点的结点值(用单个小写字母表示,用空格分隔)
第三行:每个叶子结点的结点值(用整数表示,用空格分隔)
输出
第一行:按从左到右输出所有非叶子结点
第二行:按从左到右输出所有非叶子结点对应的权值
第三行:按从左到右输出每个叶子结点
第四行:按从左到右输出每个叶子结点的哈夫曼编码
样例输入
A(B(D(F,G),E),C)
a b c d
1 2 3 4
样例输出
D B A
3 6 10
F G E C
000 001 01 1
题解
事先说明一下,我做这个题是在老师讲哈夫曼树之前,所以代码逻辑混乱、思维白给,不能代表敬爱的潘老师的教学内容。因为时间比较紧,所以这次只能挑几个题出一下题解,其他的等考完试再补上。应一位神秘同学的要求,先写这个题的题解,而我又没时间按正规思路写一遍了,所以只能硬着头皮讲当时做题时候的思路。
这个思路比较基础,是完全建立在之前学的树的基本功能至上的,所以就算你完全没懂哈夫曼树是什么,只要你能看懂题意,应该就能看懂下面的代码(虽然它真的有点长)
另外,由于它跟哈夫曼树几乎完全没关系,所以即使它提交结果是AC,但我不敢保证它的正确性。不过就算不对,下面的思路也不失为对树的基础知识的一种灵活运用~~(强行狡辩)~~
题意
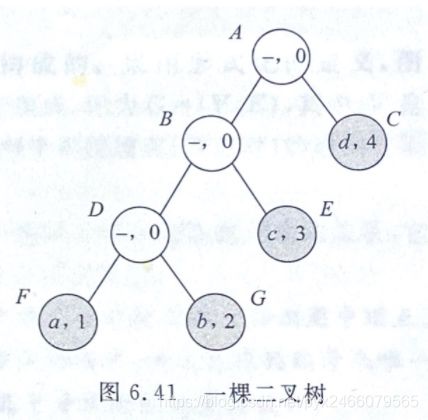
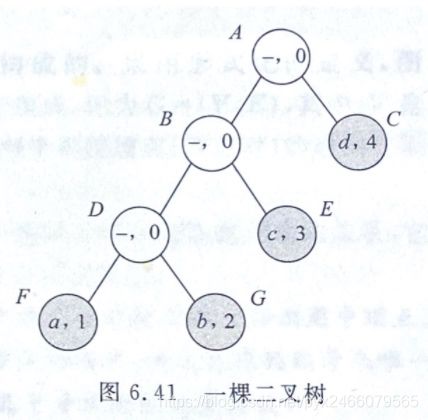
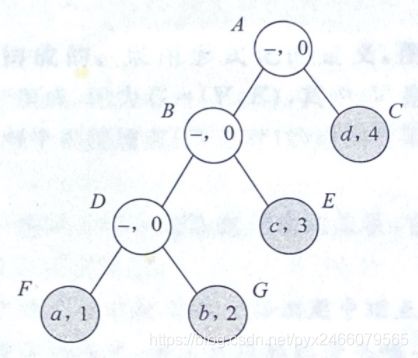
根据题意,每个“哈夫曼树”的结点都是这样的:
- 含有一个标号,是单个大写字母:
A、B、C、D、E、F、G - 含有一个结点值,是单个小写字母,其中
- 叶子结点的结点值来源于数组
v - 非叶子结点的结点值为
-
- 叶子结点的结点值来源于数组
- 含有一个权值,是一个整数,其中
- 叶子结点的权值来源于数组
w - 从输入输出样例可以看出,非叶子结点的权值等于左右孩子的权值的和
- 叶子结点的权值来源于数组
再来看题目要求:
任务1. 需要一个常用的括号表达式建树函数
任务2. 需要一个从左到右遍历叶子结点的方法
任务3. 需要一个由子结点的权值计算父节点权值的方法
任务4. 需要一个计算哈夫曼编码的方法,并运用与任务2相同的方法遍历输出
哈夫曼编码是什么?
我们可以从样例输出的规律里,观察哈夫曼编码的规则,我再把图放一遍:
样例告诉我们:
-
F结点对应哈夫曼编码000,从根结点开始找它的话,依次是:A的左孩子为B、B的左孩子为D、D的左孩子为F -
G结点对应哈夫曼编码001,从根结点开始找它,依次是:A的左孩子为B、B的左孩子为D、D的右孩子为G -
E结点对应哈夫曼编码01,从根结点开始找它,它依次是:A的左孩子为B、B的右孩子为E -
G结点对应哈夫曼编码1,从根结点开始找它,直接就是A的右孩子为D
发现了吗?只要找到从根结点到它的路径,然后按照左孩子-0、右孩子-1的规则写,就可以得到哈夫曼编码了
同时,从样例中可以看出,我们需要一种从左到右、从下到上的遍历方法,来完成这个题的任务
思路解析及对应代码
建树
用括号表达式建树的方法属于二叉树的基本操作,可以参考我之前的博客,里面有蛮详细的讲解,这里直接给代码
二叉树基础操作部分:数据结构与算法——二叉树
void CreateBTree(BTNode *&bt,char *str){
stack<BTNode*> st; //STL的栈,类型为BTNode的指针
bt=NULL; //根结点初始化为空
int k; //用k记录左右儿子,1为左,2为右
BTNode *p=NULL; //用p存储读取到的字符
int len=strlen(str); //字符串str的长度为len
for(int i=0;i<len;i++){
if(str[i]=='('){
k=1; //k计为左儿子
st.push(p); //入栈
continue;
}
else if(str[i]==')'){
st.pop(); //出栈
continue; //继续往后看
}
else if(str[i]==','){
k=2; //k计为右儿子
continue;
}
else{
p=new BTNode(); //为p申请空间
p->data=str[i]; //赋值
p->lc=p->rc=NULL;
if(bt==NULL) //如果bt为空,代表p为最开始的根结点
bt=p;
else
if(k==1) //之前读取到左括号,说明p是左孩子
st.top()->lc=p;
else if(k==2) //之前读取到逗号,说明p是右孩子
st.top()->rc=p;
}
}
}
从左到右遍历叶子结点
一看到从左到右,我们就可以联想到先序遍历,但先序遍历是遍历整棵树,无法做到只遍历叶子结点,怎么处理呢?
~~有句古话说的好,既然打不过,就加入他们吧。~~既然的确无法做到,那我们就干脆让它痛痛快快地遍历完整棵树,然后只从中利用对我们有用的部分。在每次访问结点的时候,都判断一下它是不是叶结点,如果不是就继续正常遍历,如果是就拿出来用。由于我们将会多次用到从左到右的叶子结点序列,所以干脆把它们的地址存起来,用的时候直接找数组即可
BTNode *saveLeaf[100];
int h=0; //作为saveLeaf的下标
void findLeaf(BTNode* bt){
//找叶子结点的函数findLeaf,基于先序遍历
if(bt!=NULL){
if(bt->lc==NULL&&bt->rc==NULL){
saveLeaf[h]=bt;
h++;
return;
}
findLeaf(bt->lc);
findLeaf(bt->rc);
}
}
只要执行一遍这个函数,我们就可以得到一个装有从左到右的叶子结点的指针数组。
从左到右、从下到上遍历整棵树
直接遍历我们不会,所以我们借鉴一下上个问题的解决方案:加入他们
我们做这样一个假设——假设我们可以在访问每个节点的时候,方便地知道它是第几层的节点,那么我们就可以多次进行先序遍历,第一次先序遍历只解决最后一层的问题,第二次先序遍历只解决倒数第二层的问题,以此类推,假设树的深度为dep,那么我们只要进行dep次先序遍历,就可以实现从下到上、从左到右地遍历整棵树。
这样,我们的任务又被拆成了两个小任务:
- 怎么样get每个节点的深度
- 怎么样具体实现上面的遍历
给每个节点设置深度
我们在结点的结构中加入一项——当前节点深度dep,然后专门写一个函数来给每个结点的dep赋值。
到此,结点的结构完整了,我们给出它的样子:
struct BTNode{
char data; //存大写字母
int q=-1; //存权值
char c; //存小写字母(如果有)
int dep=1; //深度
BTNode *lc,*rc; //左右孩子
};
赋值函数giveDep这样写:
void giveDep(BTNode *bt, int dep){
if(bt!=NULL){
bt->dep=dep; //赋值
dep++; //因为即将访问孩子结点,所以深度要在父节点的基础上+1
giveDep(bt->lc, dep);
giveDep(bt->rc, dep);
}
}
这样的话,在主函数中只要执行:
giveDep(bt,1); //设根结点深度为1
就可以实现给每个节点的dep赋值了
遍历
首先我们微微修改一下先序遍历,使它能识别出我们指定的层数,也就是说我们需要给函数新增一个参数Dep,然后每次访问结点的时候都把当前节点的dep和我们传入的Dep比较。所以为了一直能这么判断,传入的参数Dep在递归过程中是不可以变的。
void PreOrder2(BTNode *bt,int Dep){
if (bt!=NULL){
if(bt->dep==Dep) //判断层数是不是我们想要的
cout<<bt->data;
PreOrder2(bt->lc,Dep);
PreOrder2(bt->rc,Dep);
}
}
如此,假设树的深度为th,那么我们只要依次让第二个参数为th、th-1、…、1,就可以实现我们的目的了。
树的深度可以通过基本操作函数BTHeight得到,讲解见基础篇,这里直接给出代码:
int BTHeight(BTNode *bt){
int lch, rch; //左子树深度lch和右子树深度rch
if(bt==NULL) return 0; //如果是空的,就说明没有长度,返回0
else{
lch=BTHeight(bt->lc); //左子树的深度
rch=BTHeight(bt->rc); //右子树的深度
if(lch>rch)return lch+1;
else return rch+1;
}
}
在主函数中,我们这样写:
int h=BTHeight(bt);
for(int i=h;i>0;i--)
PreOrder(bt,i);
完事儿
逐个实现题目要求
上面写过的函数,我就直接调用了啊
用括号表示法建树
BTNode *bt;
cin>>str;
CreateBTree(bt,str);
输入数组v和u
方法不唯一,我的办法是先通过基本操作函数LeafCount获得叶子结点的个数n,再精确地输入n个字符/数
int n=LeafCount(bt);
for(int i=0;i<n;i++)
cin>>v[i];
for(int i=0;i<n;i++)
cin>>u[i];
其中基本操作函数LeafCount的讲解见基础篇,这里直接给出代码
int LeafCount(BTNode *bt){
int num1,num2;
if(bt==NULL)
return 0;
else if(bt->lc==NULL&&bt->rc==NULL)
return 1;
else{
num1=LeafCount(bt->lc);
num2=LeafCount(bt->rc);
return num1+num2;
}
}
从左到右输出非叶子结点
因为要找的是“非叶子结点”,所以我们只要基于上面的PreOrder2函数,给它添加一个判断函数是不是叶子结点的功能,就可以实现这一步的任务。因为非叶子结点也用了两次,所以我们干脆也把它们存起来。
BTNode *saveNotLeaf[100]; //用于存储
int hn=0; //下标
void findNotLeaf(BTNode *bt,int Dep){
if (bt!=NULL){
if(bt->dep==Dep&&(bt->lc!=NULL||bt->rc!=NULL)){
saveNotLeaf[hn]=bt;
hn++;
}
findNotLeaf(bt->lc,Dep);
findNotLeaf(bt->rc,Dep);
}
}
在主函数中,记得要先给每个节点的dep赋值
giveDep(bt,1); //赋值函数,还记得吧?
int th=BTHeight(bt);
for(int i=th;i>0;i--)
findNotLeaf(bt,i);
cout<<endl;
从左到右输出所有非叶子结点的权值
要有权值才可以输出呀,所以我们写一个函数计算所有节点的权值。计算权值的规则还记得吧?不记得的话就上去看看
一点都不复杂,因为有th层,执行一次先序遍历,可以求出每个有权结点的父节点权值,我们只要走th次先序遍历,就一定可以算出每个节点的权值
void giveQ(BTNode *&bt){
if(bt!=NULL&&bt->lc!=NULL&&bt->rc!=NULL){
bt->q=bt->lc->q+bt->rc->q;
//cout<data<<" - "<q<
giveQ(bt->lc);
giveQ(bt->rc);
}
}
需要注意的是,我们要先把叶子结点的权值设置好,再执行giveQ函数。主函数里:
findLeaf(bt);//找到所有的叶子结点
for(int i=0;i<h;i++)
saveLeaf[i]->q=u[i]; //给叶子结点赋权
for(int i=0;i<th;i++) //执行th次
giveQ(bt);
for(int i=0;i<hn;i++)
cout<<saveNotLeaf[i]->q<<" "; //直接调用上一问保存好的数组
cout<<endl;
从左到右输出每个叶子结点
由于在上一问里已经执行过findLeaf函数,这一问直接输出即可
for(int i=0;i<h;i++)
cout<<saveLeaf[i]->data<<" ";
cout<<endl;
至此我们已经完成了三行输出,就差一行了,加油!
输出每个叶子结点的哈夫曼编码
得先把哈夫曼编码计算出来,才能输出。
计算规则没忘吧?
我们用栈的结构来实现哈夫曼编码的计算,思路是这样的:
- 根据下一步访问的结点,将对应编码入栈:
- 访问左孩子,则
0入栈; - 访问右孩子,则
1入栈;
- 访问左孩子,则
- 如果找到对应结点的编码,结束
- 如果没找到,当前栈顶编码出栈
我们以找结点G的哈夫曼编码为例
- 访问
B,0入栈; - 访问
D,0入栈; - 访问
F,0入栈; F无法继续访问且没找到G,当前栈顶元素0出栈;- 访问
G,1入栈; - 找到
G,当前栈内序列001即为G的哈夫曼编码,输出结果
代码实现
void printSTA(stack<int> s){
//用来倒序输出栈的函数
int a[100],h=0;
while (!s.empty())
a[h++]=s.top(),s.pop();
for(int i=h-1;i>=0;i--)
cout<<a[i];
cout<<" ";
}
stack<int> ans; //栈,需要头文件主函数内:
for(int i=0;i<h;i++)
printHFM(bt,saveLeaf[i]->data);
大功告成!
最终代码
#include 关于代码完善的思路
别看字数多、代码多,但其实也没那么难
这个思路其实是简化版,只考虑了除叶子结点外,每个节点都有左右孩子的情况。更改其中的几个非叶结点判断(比如权值计算函数),就可以把范围扩展到“每个节点不一定都有右孩子,但必须有左孩子”;如果想扩展到全适用,只要在建树时假设它有,然后在处理时加一步判断,或通过给予优先级的方法处理即可。
我提交过上面的解法,也成功AC了。咱们对二叉树的要求不高,和我的解法难度类似的题一般不会考察,所以核心目的还是通过这种拐着弯儿的思路,更加熟练地运用二叉树的基本操作。
最后提醒一句:**上面的总结代码一定不要直接抄!**一共187行的代码,如果完全一样,你就等着原地去世吧!