蒙特卡洛粒子滤波定位算法_论文推荐 | 基于Huber MCKF的UUV目标跟踪算法

点击”公众号首页-论文导读-微刊”或页面下端“阅读原文”可在线浏览文章全文，如果你喜欢本文，请分享到朋友圈。 2020年第28卷第1期 基础研究 基本信息

作者: 王  斌¹,  温  泉²,  范世东¹

单位：1. 武汉理工大学 能源与动力工程学院, 湖北 武汉, 430063; 2. 长江航道规划设计研究院, 湖北 武汉, 430010

基金项目: 中央高校基本科研业务费专项资助项目(195205013).

摘要

针对无人水下航行器(UUV)目标跟踪精度不高的问题, 文中将一种鲁棒性较强的M极大似然估计代价函数引入Huber-容积卡尔曼滤波(H-CKF)并应用于UUV的目标跟踪定位算法中, 通过改变归一化新息协方差的方法对CKF矩阵进行线性化求解。建立了UUV运动模型及观测模型, 在不同的非高斯噪声干扰下与转换测量卡尔曼滤波、CKF和扩展卡尔曼滤波3种滤波算法进行对比试验, 验证了HM-CKF的滤波精度和稳定性优于传统算法。

    

无人水下航行器(unmanned undersea vehicle, UUV)技术在军事领域、渔业以及海底探测等方面正在扮演着越来越重要的角色^[1]。目前UUV的目标跟踪主要通过检测目标的有效辐射(例如声辐射和电磁辐射), 以获取目标相对于UUV的连续方位角^[2]。但是在水下恶劣情况下被动声呐的测量精度很低, 且海洋情况(海水温度、密度和盐度变化等)复杂, 噪声统计特性(平均值和协方差)未知, 估计的准确性未知。同时, 非线性的测量量存在于UUV的目标跟踪中, 给滤波算法带来了极大的困难, 因此精算滤波算法对于UUV的目标跟踪来说具有极大的工程意义^[3-5]。

目前UUV的目标跟踪方法主要有粒子滤波(particle filter, PF)、扩展卡尔曼滤波(extended Kalman filter, EKF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)及容积卡尔曼滤波(cubature Kalman fllter, CKF)等。PF依据蒙特卡洛仿真思想, 通过随机产生大量粒子来近似后验概率密度。因此粒子滤波计算量相当大, 对于实时性的要求很难满足, 且有粒子退化和贫化等问题^[6]。边信黔等^[7]将EKF算法应用到UUV的航迹推算上, 取得较好效果, 但EKF对高非线性系统的预测准确性较差, 而且需要计算雅可比矩阵, 导致计算系统复杂, 应用性不强^[8]。许多学者也提出了基于UKF的状态估计算法, 该算法的性能优于EKF, 且无需计算雅克比矩阵, 但UKF使用权值为负的Sigma点来更新矩阵, 在高维系统中准确度低, 计算复杂在工程中难以实现^[9]。Arasaratnam等^[10]提出了基于容积变换的CKF方法, 其具有编号稳定, 计算复杂度低, 操作简单等优点, 但是也不能很好地解决非高斯白噪声问题。

为此, 文中利用具有鲁棒性的M极大似然估计函数^[11]来改造Huber-CKF(H-CKF), 先通过重建CKF的测量信息, 对非线性测量信息进行滤波, 再利用高阶容积准则对该滤波框架进行近似计算, 进而得到量测噪声下的Huber M-CKF(HM-CKF)算法。这样就无须使用传统的算法来避免噪声对信息的干扰, 从而实现了滤波算法的鲁棒性。在不同的非高斯噪声干扰下与CKF、EKF、转换测量卡尔曼滤波(converted measurement Kalman filter, CMKF)进行了仿真对比试验, 验证了HM-CKF的滤波精度和稳定性更优于传统算法。

　 1   UUV运动模型建立　

1.1  运动方程

1.2  量测方程

　 2  算法描述　

2.1  EKF

2.2  CKF

2.3  HM-CKF

3   仿真结果与分析   

3.1  轨迹图对比

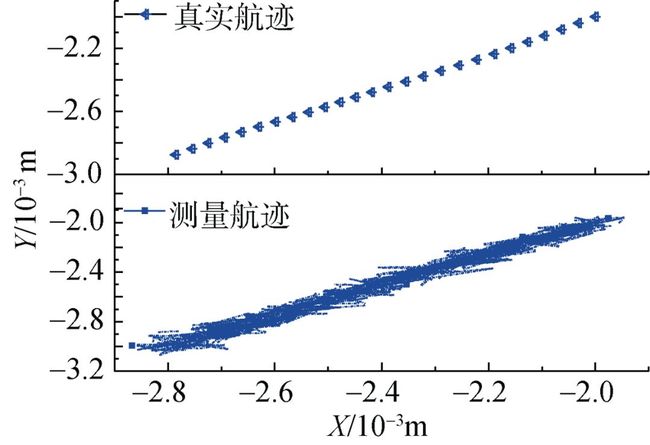
式(1)~式(5)模拟产生UUV的真实轨迹, 所得数据称之为真值, 由于此模型中所假设UUV在Z方向上速度为0, 在X-Y平面上做匀速直线运动; 但是实际应用中的声呐无法直接得到真实值, 只能得到测量值, 也就是文中数学模型中添加的噪声测量值, 由于噪声误差的存在, 声呐得到的数据可能与真实值差别很大, 其中真实轨迹和测量轨迹如图1所示, 图中, 横、纵坐标分别为大地坐标系的X和Y方向。

图1  无人水下航行器仿真航迹

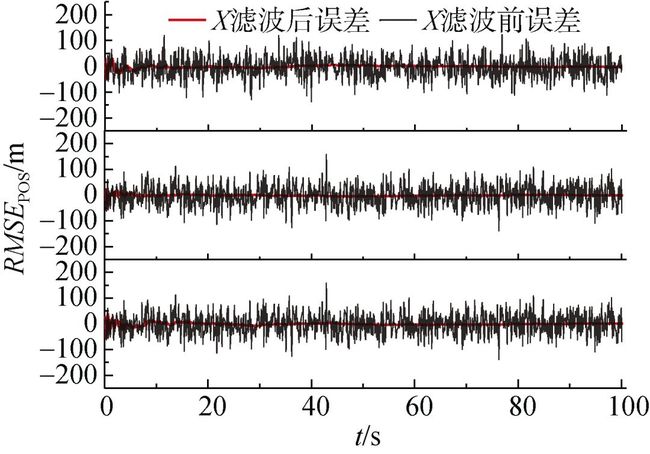
3.2  误差对比 1) 线性系统

文中在X、Y、Z这3个方向进行了仿真试验, 得到线性系统下误差对比如图2所示。

图2  各方向滤波前后误差比较

由图2可知, 滤波前的误差值(黑色曲线)在0值上下波动很大, 但经过滤波后的误差值(红色曲线)在15 s过后非常稳定, 保持在0值附近, 即在线性系统内经过卡尔曼滤波后误差显著减小。

2) 非线性系统

在高非线性系统中, 文中为突显各种滤波算法的优劣, 在3种典型的声呐工况下将4种滤波方法进行对比, 每组进行50次蒙特卡洛仿真试验。状态方程过程噪声协方差和转换测量噪声的标准差取值如表2所示^[4]。

表2  3种工况下状态方程过程噪声协方差和标准差

表中, v_r、v_β和v_ε 分别为转换测量噪声的目标距离标准差、高低角标准差和方位角标准差。

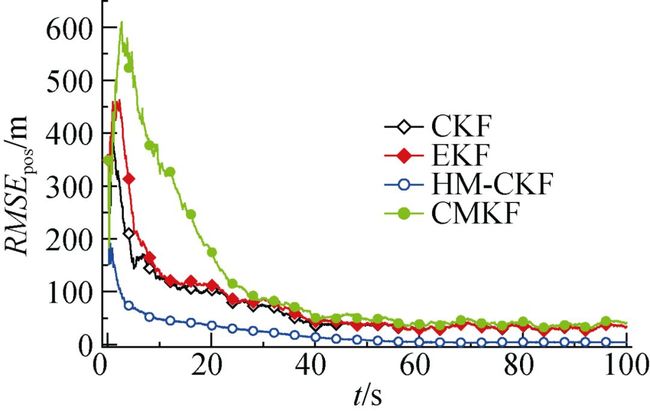
图3~图8分别给出了UUV直航情况下各滤波算法RMSE_pos对比图。

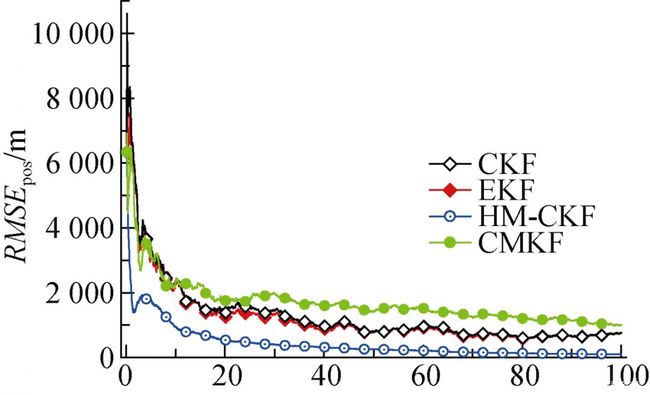
图3  工况1下各滤波算法位置均方根误差(RMSE_pos)对 比曲线

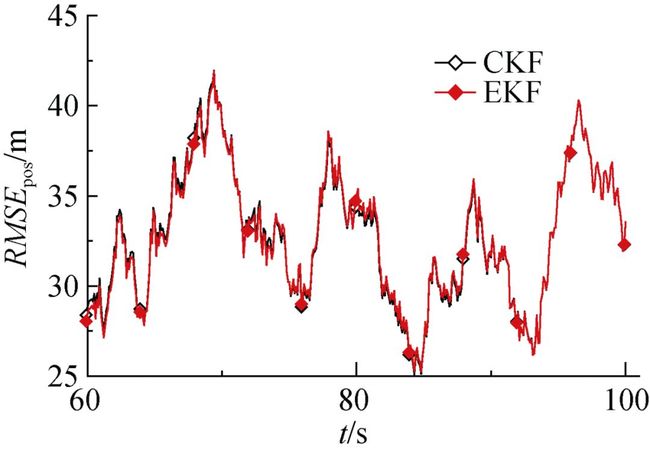
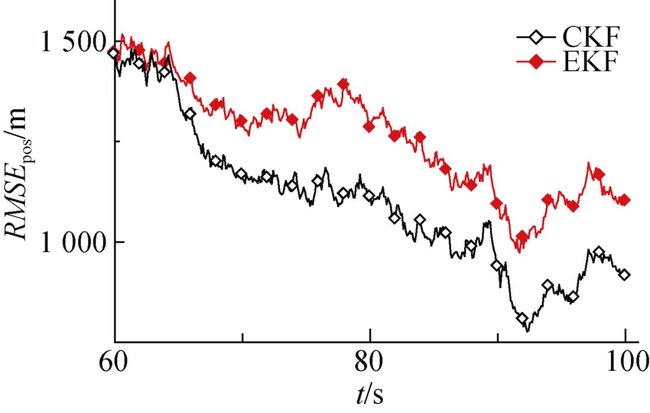
图4  工况1下容积卡尔曼滤波和扩展卡尔曼滤波的RMSE_pos放大曲线

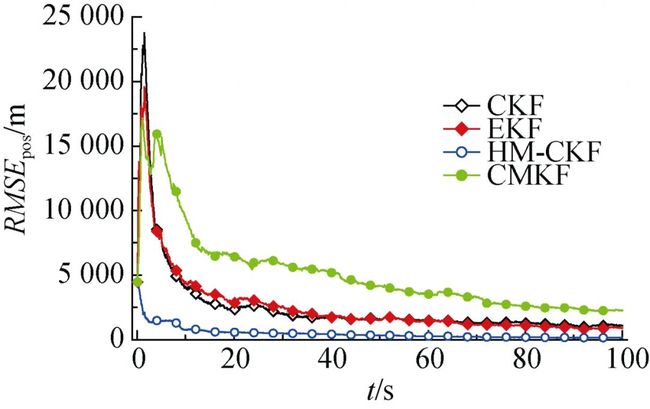
图5  工况2下各滤波算法RMSE_pos对比曲线

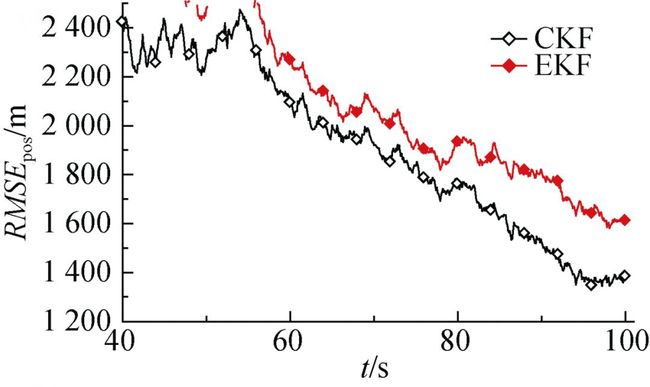
图6  工况2下CKF和EKF的RMSE_pos放大曲线

图7  工况3下各滤波算法RMSE_pos对比曲线

图8  工况3下CKF和EKF的RMSE_pos放大曲线

由上图可知, 在高非线性系统内CMKF已经发散, 位置误差值偏大, 在工程应用上表现不佳。相比较于CMKF, EKF和CKF收敛速度明显加快, 数值也比较稳定, 在低噪声条件下平均位置误差值稳定在50 m内, 在高噪声条件下平均位置误差值稳定在1 000 m以内, 工程上表现良好; 但EKF和CKF还是存在很大不足, 2种滤波算法在高噪声条件下的平均位置误差超过500 m, 无法再减小, 性能不如HM-CKF。

从收敛速度方面分析, HM-CKF从20 s左右已经开始收敛, EKF和CKF则从30 s左右才开始收敛, 前者收敛速度明显更快; 从平均位置误差值方面分析, HM-CKF最后收敛的误差值明显小于EKF和CKF的收敛误差值。

通过前面理论分析和仿真案列, 可得到如下结论:

1) 卡尔曼滤波在处理线性系统误差方面性能优异, 但在非线性系统内性能不佳;

2) 在低噪声状况下, CKF无论在收敛速度或是位置误差值方面都优于EKF, 但在高噪声条件下二者性能差别不明显;

3) HM-CKF在水下目标的信号收集处理方面表现良好, 极大地减小了位置误差, 且比CKF和EKF收敛速度更快, 位置误差数值更小, 同时HM-CKF的数值稳定性和跟踪精度更高。

4   结束语   

文中基于鲁棒性较强的Huber M极大似然估计代价函数, 针对H-CKF算法在复杂的非高斯噪声环境下估计精度不高的问题, 进行了求解优化和仿真验证。仿真结果显示, 在含复杂非高斯噪声的环境下, HM-CKF较CMKF、CKF和EKF,的数据曲线明显收敛更快、更稳定, 误差更小, 在非线性系统中其适用性更强。但在实际工程中, 有色噪声干扰往往比较大, HM-CKF虽比传统滤波算法表现得更为稳定, 但绝对精度却并不太高, 接下来的研究将着重优化HM-CKF算法的精度。

参考文献

[1] 李永龙, 王皓冉, 张华. 水下机器人在水利水电工程检测中的应用现状及发展趋势[J]. 中国水利水电科学研究院学报, 2018, 16(6): 586-590.

Li Yong-long, Wang Hao-ran, Zhang Hua. Application St- atus and Development Trend of Underwater Robot in Wat- er and Hydropower Engineering Detection[J]. Journal of China Institute of Water Resources and Hydropower Research, 2018, 16(6): 586-590.

[2] 庞硕, 纠海峰. 智能水下机器人研究进展[J]. 科技导报, 2015, 33(23): 66-71.

Pang Shuo, Jiu Hai-feng. Current Statue of Autonomous Underwater Vehicles Research and Development[J]. Science & Technology Review, 2015, 33(23): 66-71.

[3] 张铁栋, 万磊, 王博, 等. 基于改进粒子滤波算法的水下目标跟踪[J]. 上海交通大学学报, 2012, 46(6): 943- 948.

Zhang Tie-dong, Wan Lei, Wang Bo, et al. Underwater Object Tracking Based on Improved Particle Filter[J]. Jo- urnal of Shanghai Jiaotong University, 2012, 46(6): 943- 948.

[4] Xu J, Xu M, Zhou X. The Bearing Only Target Tracking of UUV Based on Cubature Kalman Filter with Noise Es-timator[C]//2017 36th Chinese Control Conference(CCC). Dalian, China: IEEE, 2017: 5288-5293. 

[5] 王艳艳, 刘开周, 封锡盛. 基于强跟踪平方根容积卡尔曼滤波的纯方位目标运动分析方法[J]. 计算机测量与控制, 2016, 24(11): 136-140.

Wang Yan-yan, Liu Kai-zhou, Feng Xi-sheng. Bearings Only Target Motion Analysis Based on Strong Tracking Square-Root Cubature Kalman Filter[J]. Computer Meas-urement & Control, 2016, 24(11): 136-140.

[6] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45.

[7] 边信黔, 周佳加, 严浙平, 等. 基于EKF的无人潜航器航位推算算法[J]. 华中科技大学学报: 自然科学版, 2011, 39(3): 100-104.

Bian Xin-chan, Zhou Jia-jia, Yan Zhe-ping, et al. Dead Reckoning Method for Autonomous Underwater Vehicles Based on EKF[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(3): 100-104.

[8] Leong P H, Arulampalam S, Lamahewa T A, et al. A Gaussian-sum Based Cubature Kalman Filter for Bearings-only Tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1161-1176. 

[9] Li P, Zhang T, Bo M. Unscented Kalman Filter for Visual Curve Tracking[J]. Image & Vision Computing, 2004, 22(2): 157-164.

[10] Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[11] 邓先瑞, 聂雪媛, 刘国平. WSNs下移动机器人HuberM-CKF离散滤波定位[J]. 计算机应用研究, 2016, 33(6):  1839-1842.

Deng Xian-rui, Nie Xue-yuan, Liu Guo-ping. Discrete HuberM-CKF Filter Based Mobile Robot Positioning in WSNs[J]. Application Research of Computers, 2016, 33 (6): 1839-1842.

[12] Donoho D L, Montanari A. Variance Breakdown of Huber (M)-estimators: n/p→m∈(1, ∞)[J]. Annals of Statistics, 2015. arXiv: 1503.02106vl.

[13] Li W, Swetits J J. The Linear L1 Estimator and the Huber m-estimator[J]. SIAM Journal on Optimization, 1998, 8 (2): 457-475.

[14] 刘星成, 袁东升, 梁平元, 等. 基于代价函数的WSN能R效路由协议性能分析[J]. 通信学报, 2011, 32(6): 132- 140.

Liu Xing-cheng, Yuan Dong-sheng, Liang Ping-yuan, et al. Performance Analysis of Cost Function Based energy-efficient Routing Protocol in WSN[J]. Journal on Communications, 2011, 32(6): 132-140.

[15] 李晓兰. 我国引进深海水下机器人“海狮”号[J]. 海洋石油, 2009, 29(4): 103.

 原文刊登于《水下无人系统学报》2020年第28卷第1期

  武汉加油！中国加油！ E ND 水下无人系统学报

通信地址：陕西省西安市锦业路96号

E-mail：[email protected]

官方网站：www.yljszz.cn

QQ：767358370

电话：029-88327279