力扣刷题 | 双指针
文章目录
-
-
-
- 3 无重复字符的最长子串
- 11 盛更多水的容器
- 15 三数之和
- 16 最接近的三数之和
- 19 删除链表的倒数第 N 个节点
- 26 删除排序数组中的重复项
- 30 串联所有单词的子串
- 76 最小覆盖子串
- 80 删除排序数组中的重复项 II
- 86 分隔链表
- 88 合并两个有序数组
- 125 验证回文串
-
-
3 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
解法: 双指针,分别指向当前最长子串的开始和结尾,每次将后面的指针向后移动一格,检查是否重复,如有重复,将前面的指针向后移动,直至无重复为止,比较每次子串长度,记录最大值
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if len(s) == 0:
return 0
i = 0
j = 0
ans = 0
str_map = {
}
while j < len(s):
if s[j] not in str_map:
ans = max(ans, j-i+1)
str_map[s[j]] = j
j += 1
else:
del str_map[s[i]]
i += 1
return ans
11 盛更多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
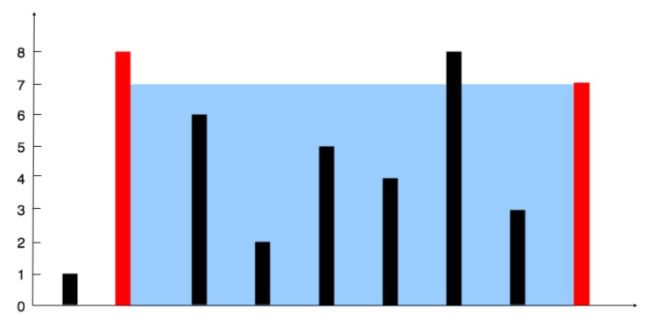
示例:下图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
解法: 双指针,分别从两边向中间移动,每次移动对应高度较小的那个,比较盛水的多少,记录最大值,直至两个指针相遇。
移动对应高度较小的指针是因为,这个较小的指针不可能和两个指针之间的柱子一起组成盛更多水的容器。盛水量=盛水高度*盛水宽度,盛水高度由边界中的较小值决定,如果移动较大的指针,无论移动后对应的柱子多高,盛水高度都不可能增加,只可能减少,且盛水宽度减少,故盛水量减少。
class Solution:
def maxArea(self, height: List[int]) -> int:
i, j = 0, len(height)-1
ans = min(height[i], height[j]) * (j-i)
while j > i+1:
if height[i] < height[j]:
i += 1
else:
j -= 1
ans = max(ans, min(height[i], height[j]) * (j-i))
return ans
15 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
解法: 采用双指针,首先固定第一个元素,然后移动另外两个指针,找满足条件的三元组。注意在移动第一个元素和移动指针时,重复元素应跳过
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
if len(nums) < 3:
return [] # 注意此处不是返回 None,而是空列表
nums.sort()
ans = list()
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i-1]:
continue
j = i+1
k = len(nums)-1
while k > j:
if nums[i] + nums[j] + nums[k] > 0:
k -= 1
while k > j and nums[k] == nums[k+1]:
k -= 1
elif nums[i] + nums[j] + nums[k] < 0:
j += 1
while k > j and nums[j] == nums[j-1]:
j += 1
else:
ans.append([nums[i], nums[j], nums[k]])
k -= 1
while k > j and nums[k] == nums[k+1]:
k -= 1
return ans
16 最接近的三数之和
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示:
3 <= nums.length <= 10^3
-10^3 <= nums[i] <= 10^3
-10^4 <= target <= 10^4
解法: 采用双指针,首先固定第一个元素,然后移动另外两个指针,找三元组并记录结果
class Solution:
def threeSumClosest(self, nums: List[int], target: int):
nums.sort()
bias = abs(sum(nums[0:3])-target)
ans = sum(nums[0:3])
for i in range(len(nums)-2):
if i > 0 and nums[i-1] == nums[i]:
continue
j = i+1
k = len(nums)-1
while k > j:
bias_temp = nums[i] + nums[j] + nums[k] - target
if abs(bias_temp) == 0:
return bias_temp + target
elif abs(bias_temp) < bias:
ans = bias_temp + target
bias = abs(bias_temp)
if bias_temp > 0:
k -= 1
else:
j += 1
return ans
19 删除链表的倒数第 N 个节点
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。给定的 n 保证是有效的。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
解法: 利用双指针,先移动第一个到第 n 个位置,再同步移动两个指针,直到第一个指针到头。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int):
p = ListNode(-1)
p.next, a, b, m = head, p, p, 0
while m < n:
b = b.next
m += 1
while b.next:
a = a.next
b = b.next
a.next = a.next.next
return p.next
26 删除排序数组中的重复项
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
解法: 双指针,遇到重复值后面的指针向后移动,否则前面的指针向后移动,并将后面的指针对应的值复制到前面
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
if len(nums) <= 1:
return len(nums)
i = 0
j = 1
while j < len(nums):
if nums[j] == nums[i]:
j += 1
else:
i += 1
nums[i] = nums[j]
return i+1
30 串联所有单词的子串
给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 words 中的单词完全匹配,中间不能有其他字符,但不需要考虑 words 中单词串联的顺序。
示例 1:
输入:
s = “barfoothefoobarman”,
words = [“foo”,“bar”]
输出:[0,9]
解释:
从索引 0 和 9 开始的子串分别是 “barfoo” 和 “foobar” 。
输出的顺序不重要, [9,0] 也是有效答案。
示例 2:
输入:
s = “wordgoodgoodgoodbestword”,
words = [“word”,“good”,“best”,“word”]
输出:[]
解法: 滑动窗口,逐一检查字符串是否满足条件
待优化:
- 可以采用哈希表的方式来判断子串中每个单词出现了几次
- 可以将窗口每次滑动一个单位改为每次滑动单词长度个单位
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
if len(words) == 0 or len(words[0]) == 0:
return list(range(len(s)))
if len(s) < len(words[0]):
return []
words_num, word_len = len(words), len(words[0])
i = 0
ans = list()
while i < len(s)-words_num*word_len+1:
words_temp = words[:]
j = 0
while words_temp and s[(i+j*word_len):(i+(j+1)*word_len)] in words_temp:
words_temp.remove(s[(i+j*word_len):(i+(j+1)*word_len)])
j += 1
if j == words_num:
ans.append(i)
i += 1
return ans
76 最小覆盖子串
给你一个字符串 S、一个字符串 T 。请你设计一种算法,可以在 O(n) 的时间复杂度内,从字符串 S 里面找出:包含 T 所有字符的最小子串。
示例:
输入:S = “ADOBECODEBANC”, T = “ABC”
输出:“BANC”
提示:
如果 S 中不存这样的子串,则返回空字符串 “”。
如果 S 中存在这样的子串,我们保证它是唯一的答案。
解法: 双指针,左右指针都从0位置开始,每次右指针向后移动一个,如左右指针之间的字符串满足条件,则将左指针向后移动一个,指针移动过程中记录答案
class Solution:
def minWindow(self, s: str, t: str) -> str:
def check(cnt, ori):
for k, v in ori.items():
if k not in cnt.keys() or cnt[k] < v:
return False
return True
if len(s) == 0 or len(t) == 0:
return ""
cnt, ori = {
}, {
}
l, r, l_ans, r_ans, len_ans = 0, 0, 0, 0, len(s)
find_label = False
for t1 in t:
ori[t1] = (ori[t1] + 1) if t1 in ori.keys() else 1
while r < len(s):
cnt[s[r]] = (cnt[s[r]] + 1) if s[r] in cnt.keys() else 1
while check(cnt, ori) and l <= r:
if r-l+1 <= len_ans:
l_ans, r_ans, len_ans = l, r, r-l+1
find_label = True
cnt[s[l]] -= 1
l += 1
r += 1
return s[l_ans:(r_ans+1)] if find_label else ""
80 删除排序数组中的重复项 II
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素最多出现两次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定 nums = [1,1,1,2,2,3],
函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,1,2,3,3],
函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。
你不需要考虑数组中超出新长度后面的元素。
解法: 双指针,右指针维护当前判断的值的位置,左指针维护无重复项的数组的终点,通过布尔型变量 repeat 记录左指针当前项是否重复过,若左右指针的值不相等或二者值相等但左指针的值未重复过,则将左指针向后移动一格,右指针的值存入左指针所在的位置
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
if len(nums) <= 2:
return len(nums)
l, r, repeat = 0, 1, False
while r < len(nums):
if nums[r] == nums[l]:
if not repeat:
l += 1
nums[l] = nums[r]
repeat = True
else:
l += 1
nums[l] = nums[r]
repeat = False
r += 1
return l+1
86 分隔链表
给定一个链表和一个特定值 x,对链表进行分隔,使得所有小于 x 的节点都在大于或等于 x 的节点之前。
你应当保留两个分区中每个节点的初始相对位置。
示例:
输入: head = 1->4->3->2->5->2, x = 3
输出: 1->2->2->4->3->5
解法: 双指针,右指针维护当前判断的值的上一位置,左指针维护最右的小于x的值的位置,如果右指针下一位置的值小于x,则调整链表
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
if not head or not head.next:
return head
l = ListNode(x-1)
l.next = head
ans, r = l, l
while r.next:
if r.next.val < x:
if r.val >= x:
l_next, r_next, r_next_next = l.next, r.next, r.next.next
r_next.next, r.next = ListNode(), r_next_next
l.next = r_next
l.next.next = l_next
l = l.next
else:
r = r.next
l = l.next
else:
r = r.next
return ans.next
88 合并两个有序数组
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
解法: 双指针,比较大小存入对应位置,注意,指针从尾部逐渐向前移动,可以避免额外的 O ( m ) O(m) O(m)空间复杂度
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
p, q = m-1, n-1
while p >= 0 or q >= 0:
if q < 0:
break
elif p < 0:
nums1[q] = nums2[q]
q -= 1
else:
if nums1[p] < nums2[q]:
nums1[p+q+1] = nums2[q]
q -= 1
else:
nums1[p+q+1] = nums1[p]
p -= 1
125 验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: “A man, a plan, a canal: Panama”
输出: true
示例 2:
输入: “race a car”
输出: false
解法: 双指针
class Solution:
def isPalindrome(self, s: str) -> bool:
l, r = 0, len(s)-1
while r-l > 0:
while l <= len(s)-1 and not s[l].isalnum():
l += 1
while r >= 0 and not s[r].isalnum():
r -= 1
if l <= len(s)-1 and r >= 0 and s[l].lower() != s[r].lower():
return False
l += 1
r -= 1
return True