2020 蓝桥杯 C/C++实现 7月C组省赛
题目列表
- 试题 A: 指数计算
- 试题 B: 解密
- 试题 C: 跑步训练
- 试题 D: 合并检测
- 试题 E: REPEAT 程序
- 试题 F: 分类计数
- 试题 G: 整除序列
- 试题 H: 走方格
- 试题 I: 字符串编码
- 试题 J: 整数小拼接
试题 A: 指数计算
本题总分:5 分
问题:
请计算:7 ^ 2020 mod 1921,其中 A mod B 表示 A 除以 B 的余数。
思路: 快速幂。
答案: 480
#include试题 B: 解密
本题总分:5 分
问题:
小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的字符 Tc。下表给出了字符变换的规则:
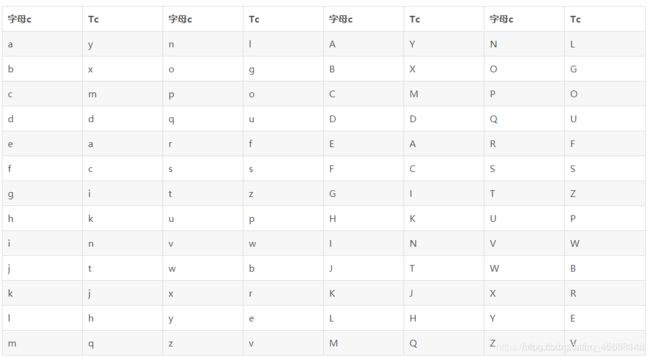
例如,将字符串 YeRi 加密可得字符串 EaFn。小明有一个随机的字符串,加密后为EaFnjISplhFviDhwFbEjRjfIBBkRyY(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符串,后面 52 行依次为表格中的内容。)
思路: 因为我没有文本形式的这个对照表。。。所以用的最笨的方法。
答案: YeRikGSunlRzgDlvRwYkXkrGWWhXaA
#include试题 C: 跑步训练
本题总分:10 分
问题:
小明要做一个跑步训练。
初始时,小明充满体力,体力值计为 10000。如果小明跑步,每分钟损耗600 的体力。如果小明休息,每分钟增加 300 的体力。体力的损耗和增加都是均匀变化的。
小明打算跑一分钟、休息一分钟、再跑一分钟、再休息一分钟……如此循环。如果某个时刻小明的体力到达 0,他就停止锻炼。
请问小明在多久后停止锻炼。为了使答案为整数,请以秒为单位输出答案。
答案中只填写数,不填写单位。
思路: 简单循环即可。
答案: 3880
#include试题 D: 合并检测
本题总分:10 分
问题:
新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准 备给大量民众进病毒核酸检测。
然而,用于检测的试剂盒紧缺。 为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k 个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k 个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明 至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看, 如果检测前 k−1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中 不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用 了 k + 1 个试剂盒完成了 k 个人的检测。
A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能 最节省试剂盒?
思路: 假设有一共检测m个人,则第一批检测需要m/k个试剂盒(向上取整)。由于感染率为1%,且均匀分布,则有0.01 * m个试剂盒会有阳性反应。这时进行第二批挨个检测,检测盒数量即为0.01 * m * k个。
则总需求盒子数即为m/k+0.01 * m * k个(m/k向上取整)。
答案: 10
#include试题 E: REPEAT 程序
本题总分:15 分
问题:
附件 prog.txt 中是一个用某种语言写的程序。
prog.txt 附件下载地址
其中 REPEAT k 表示一个次数为 k 的循环。循环控制的范围由缩进表达,从次行开始连续的缩进比该行多的(前面的空白更长的)为循环包含的内容。
例如如下片段:

A = A + 4 所在的行到 A = A + 8 所在的行都在第一行的循环两次中。
REPEAT 6: 所在的行到 A = A + 7 所在的行都在 REPEAT 5: 循环中。
A = A + 5 实际总共的循环次数是 2 × 5 × 6 = 60 次。
请问该程序执行完毕之后,A 的值是多少?
思路: 可以建立一个栈来存放循环的信息,一个变量times存放当前行数被执行的次数。通过对文本的观察我们发现,可以通过每一行前面的空格数量来判断当前行数的“等级”,4个空格代表一个等级。如果当前行等级比上一层循环的等级低则说明退出了上一层循环,对栈和times进行改变即可。随后我们发现整个文本里面,所有数字都为单位数,所以我们直接用循环找到一个数字即可提取出该行的有效数字。
答案: 241830
#include试题 F: 分类计数
时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
问题:
输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字母,多少个数字。
输入:
输入一行包含一个字符串。
输出:
输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
样例输入:
1+a=Aab
样例输出:
1
3
1
思路: 简单循环。
代码:
#include试题 G: 整除序列
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
问题:
有一个序列,序列的第一个数是 n,后面的每个数是前一个数整除 2,请输出这个序列中值为正数的项。
输入:
输入一行包含一个整数 n。
输出:
输出一行,包含多个整数,相邻的整数之间用一个空格分隔,表示答案。
样例输入:
20
样例输出:
20 10 5 2 1
评测用例规模与约定:
对于 80% 的评测用例,1 ≤ n ≤ 10的9次方。
对于所有评测用例,1 ≤ n ≤ 10的18次方。
思路: 简单循环即可。
代码:
#include试题 H: 走方格
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
问题:
在平面上有一些二维的点阵。这些点的编号就像二维数组的编号一样,从上到下依次为第 1 至第 n 行,从左到右依次为第 1 至第 m 列,每一个点可以用行号和列号来表示。现在有个人站在第 1 行第 1 列,要走到第 n 行第 m 列。只能向右或者向下走。
注意,如果行号和列数都是偶数,不能走入这一格中。问有多少种方案。
输入:
输入一行包含两个整数 n, m。
输出:
输出一个整数,表示答案。
样例输入1:
3 4
样例输出1:
2
样例输入2:
6 6
样例输出2:
0
评测用例规模与约定:
对于所有评测用例,1 ≤ n ≤ 30, 1 ≤ m ≤ 30。
思路: dfs暴力搜索的话,当n=29,m=30的时候应该会超时。我们可以用dp把结果都记录下来然后直接输出。记得行号列号都是偶数的时候跳过,因为不能走入这种方格。
代码:
- dfs写法
#include- dp写法
#include试题 I: 字符串编码
时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分
问题:
小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, … Z →26。
这样一个字符串就能被转化成一个数字序列:
比如 ABCXYZ → 123242526。
现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字符串。
输入:
一个数字序列。
输出:
一个只包含大写字母的字符串,代表答案
样例输入:
123242526
样例输出:
LCXYZ
评测用例规模与约定
对于 20% 的评测用例,输入的长度不超过 20。
对于所有评测用例,输入的长度不超过 200000。
思路: 多条件判定,连着两个数和大于26的单个输出,后数第两个值为0的单个输出…大概要点好像就这么多,欢迎补充。
代码:
#include试题 J: 整数小拼接
时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分
问题:
给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i不等于 j),然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 可以拼成 12345 或 34512 。注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法,即便是 Ai = Aj 时。请你计算有多少种拼法满足拼出的整数小于等于 K。
输入:
第一行包含 2 个整数 n 和 K。
第二行包含 n 个整数 A1, A2, · · · , An。
输出:
一个整数代表答案。
样例输入:
4 33
1 2 3 4
样例输出:
8
评测用例规模与约定:
对于 30% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ K ≤ 10的8次方, 1 ≤ Ai ≤ 10的四次方。
对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ K ≤ 10的十次方,1 ≤ Ai ≤ 10的九次方。
思路: 暴力求解应该只能过30%样例。我的思路是在第一次接收数组的时候,直接再次按位数存到二维数组里。在接下来的判断中,两个数的位数相加小于K的位数的话,就是合法值。两个数的位数相加等于K的时候再相加准确计算,由于数据最大为十的十次方,所以用long long存。
这样的思路应该能比直接暴力快不少,评测点应该能多过几个,但是能不能AC我也不清楚,毕竟现在也没样例数据。如果大佬们有好的思路,麻烦指导下谢谢。
代码:
#include
if(array[now]*pow(10,k_count-temp)+mymap[k_count-temp][now1]<=k)//两数相加小于等于k
{
ans++;
}
}
if(temp==k_count-temp&&array[now]*pow(10,k_count-temp)+array[now]<=k)//重复计数 减一个
{
ans--;
}
}
printf("%d",ans);
return 0;
}