Python算法基础题目

border="0" width="330" height="86" src="//music.163.com/outchain/player?type=2&id=472149206&auto=1&height=66">

本篇文章内容是我从曾经的笔试题或者面试题中筛选出来的
时间有点久远-------------------

苹果2014年笔试题

“逻辑学家们围成一圈坐着，他们的额头上面画有数字……”
又来一个逻辑学家围成一圈的问题，这次是这样的，三个拥有完美逻辑推理能力的人围成一圈坐在一个房间里，每个人的额头上都画着一个大于0的数字，三个人的数字各不相同，每个人都看得见其他两个人的数字，看不见自己的。
这三个数字的情况是，其中一个数字是其他两个数字的和，已知的情况还有，其中一个逻辑学家的数字是20，一个是30。
游戏组织者从这三个逻辑学家后面走过，并问三个人各自额头上的数字是什么。但第一轮每个逻辑学家都回答他们无法推测自己的数字是什么。游戏组织者只好进行第二轮的发问，这是为什么?你能据此猜出三个逻辑学家的数字吗?

答案：
结果由第三个逻辑学家的答案而定。他们三个的数字分别是20，30和50。
假设第二个和第三个逻辑学家额头上的数字是20和30，这时候如果第一个逻辑学家的数字是10，那么第二个逻辑学家看到其他两个人一个是10，一个是30，会想：“我要么是20，要么是40.”
第三个逻辑学家看到其他两个人一个是10，一个是20，会想：“我要么是30，要么是10，但我不会是10，因为每个数字都不一样，所以我应该是30.”
这样第三个逻辑学家就会猜出自己的数字是30了，但他没有，第一轮谁也没有准确推测出自己的数字，这说明我们的前提不正确，第一个逻辑学家的数字不是10，那么他只能是50。

2012年360笔试题

输出一个随机数。使用 random 模块。随机生成4到5的随机数和随机整数

import random
print(random.uniform(4, 5))
print(random.randint(4, 5))

华为python面试题

Python是如何进行内存管理的:

Python内存空间是以Python私有堆的形式进行管理的。所有的Python对象和数据结构都存放在一个私有堆中。解释器可以访问私有堆，而程序员不可以。
将Python堆空间中的内存分配给Python对象的工作是由Python内存管理器完成的。而内核API则会提供给程序员一些相关的工具来完成涉及到内存的编码工作。
Python还内置垃圾回收器，从而进行回收释放内存到堆空间。

苹果2014笔试题

你有一个横6竖6的方格……
你现在在左上第一个格子里，你的任务是移动到最右下脚的格子里，你每次只能向右或者向下移动，不能斜向移动，也不能后退。
你能找出几种方法移动到最右下脚的格子?

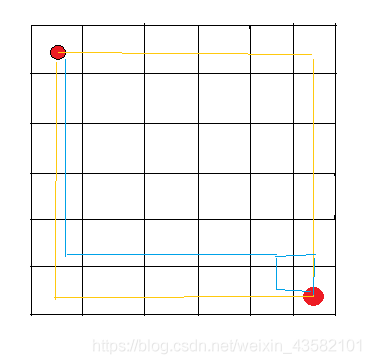
答案：
252种。
　　从对称的角度思考这个问题。
　　随便挑选一个格子，假设你从出发点有n种方法从到达与所选格子上边相邻的格子，m种方法到达与它左边相邻的格子。
　　想想看，从出发点到达一个格子的方法与到达它左边和上边的格子的方法有什么关系?说对了，由于你只能向右和向下移动，到达一个格子，不是从它左边来，就是从它上边来。
　　所以你从出发点到达一个格子的方法等于到达它上边格子的方法好到达它左边格子的方法的和相同，也就是n+m.

苹果2014年笔试题

“你有一个立方体，立方体的边长是3……”
　　这个问题比前面那个从左上格子走到右下格子的问题难，因为那毕竟是个平面问题。如图所示，这次的任务是从立方体的背面左上的小立方体走到完全相对的正面右下小立方体。
　　你可以往上移，也可以往下移，还可以往前移。
　　问题还是，你共有几种走法?

答案：
90种，思路是将这个立方体分成“三层”。
上面平面图的那道题的思路就是个最好的提示。你可以将这个立方体分成“三层”，粉红色代表最上面那层，紫色代表中间那层，橘红色代表下面那层。
现在，我们把问题变成了：从左边、右边和上边到达目标小立方体的走法共有多少(如图所示，即到达紫色中间层最右下脚方块以及橘红色最右下脚左边以及上边相邻方块的方法)?假设从起点小立方体到达终点小立方体左边相邻小立方体共有m种方法，到达右边相邻小立方体共有n种方法，到达上边相邻小立方体有r种方法，那我们需要求出来的，就是n+m+r.

用python写杨辉三角

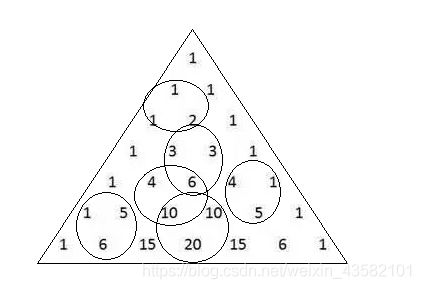
先看一下规律：
1、每行开始和结尾都是1
2、每行的数都是从两边都中间逐步变大（除第一、二行外）
3、从第三行开始，每个数都等于上方两个数之和
4、第n行有n个项
5、每行的数字之和为2的n-1次方

def angle(n):
    L=[1]
    while True:
        yield L
        L.append(0)
        L = [L[i-1]+ L[i] for i in range(len(L))]
        if len(L)>n:
            break
m = angle(7)
for i in m:
    print(i)

变态台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级…它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳发。
要求：一行代码完成
使用lambda方法
思路：
如果楼梯数已为0，则表明只有这一种跳法，也就是没有下一步的跳法了；若不为0，则设这一步会跳1、2、3~n阶，然后将跳完这一步的下一步跳法的跳法相加，返回结果。

f = lambda n: n if n < 2 else 2 * f(n - 1)

回数的查找

回数是指从左到右和从右到左的数值一样，例如：像12321这样的数，从左边1-2-3-2-1，从右边1-2-3-2-1.
要求：从100到1000的回数个数
思路：反转，列表中的三种反转分别是reversed(),sorted()，切片，而字符串中没有reverse函数，所以使用切片比较方便点。
对比切片后的，并进行判断这里用到了filter起到过滤的作用，后面在统计。

def fn(n):
    if str(n)[::-1]==str(n):
        return True
    else:
        return False
c = 0
for i in (filter(fn, range(100, 1000))):
    c+=1
print(c)

列表求和

题目：一行代码实现对列表中的偶数位置的元素进行加4后求和？
要求：一行代码实现

a = [11, 22, 33, 44, 55]
print(sum([i + 4 for i in a[1::2]]))

百度面试题

以下的代码的输出将是什么? 说出你的答案并解释？
def div1(x,y):
print("%s/%s = %s" % (x, y, x/y))

def div2(x,y):
print("%s//%s = %s" % (x, y, x//y))

div1(5,2)
div1(5.,2)
div2(5,2)
div2(5.,2.)
答案：在 Python 3中。

5/2 = 2.5
5.0/2 = 2.5
5//2 = 2
5.0//2.0 = 2.0

矩形覆盖

我们可以用 2 * 1 的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2 * 1的小矩形无重叠地覆盖一个2 * n的大矩形，总共有多少种方法？

第2*n个矩形的覆盖方法等于第2*(n-1)加上第2*(n-2)的方法。
f = lambda n: 1 if n < 2 else 2*(n - 1) + 2*(n - 2)

百度面试

题目：去除列表中的重复元素
要求：使用集合，字典，列表等方法实现
答案：

用集合

list(set(l))

用字典

l1 = ['b','c','d','b','c','a','a']
l2 = {}.fromkeys(l1).keys()

列表推导式

l1 = ['b','c','d','b','c','a','a']
l2 = []
[l2.append(i) for i in l1 if not i in l2]

Python 字典 fromkeys() 函数用于创建一个新字典，以序列 seq 中元素做字典的键，value
为字典所有键对应的初始值。该方法返回列表

fromkeys()方法语法：

dict.fromkeys(seq[, value])

百度面试

题目：有9个正方形，边长分别为1，4，7，8，9，10，14，15，18将他们拼成一个长方形，请问最长的宽为多少?
答案：
可以考虑总面积为1的平方+4的平方+7的平方 +18的平方=1056然后找能整除的数，然后再看能不能用上面的正方形的边长加出来，找到的是33和32所以这个长方形长33,宽32

阿里巴巴面试题（分类：基础）

题目：有一家公司要提高利润，有三个方案，第一个是先提高m%,再此基础上再提高n%。第二个方案是先提高n%,再此基础上再提高m%,第三个方案是每次都提高(m+n)/2%，请问哪种方 案提高利润最多?
思路：
设原来的利润为x，则第一种的结果是x(1+m%)(1+n%)
第二种的结果是x(1+n%)(1+m%)
这两种结果一样
第三种是x(1+(m+n)/2)(1+(m+n)/2)
随便假设m=2,n=4，代进去算看出第三种结果最大，所以选第三种，当然答题的时候最好简化下第三个式子，然后用它减去前面两种的结果，答案大于0就说 明他最大

解析完全平方数

题目：一个整数，它加上100和加上268后都是一个完全平方数
提问：请问该数是多少？
分析：在10000以内判断，将该数加上100后再开方，加上268后再开方，如果开方后的结果满足如下条件，即是结果。
答案：

import math
for i in range(10000):
    x = int(math.sqrt(i + 100))
    y = int(math.sqrt(i + 268))
    if x*x ==(i + 100) and y*y ==(i + 268):
        print(i)

Python回推与递推

题目：已知有五位朋友在一起。第五位朋友他说自己比第4个人大2岁；问第4个人岁数，他说比第3个人大2岁；问第三个人，又说比第2人大两岁；问第2个人，说比第一个人大两岁；最后问第一个人，他说是10岁。
要求：
求第5个人的年龄是多少。
思路：这里又是要用到利用递归的方法来解决这道题了。递归分为回推和递推两个阶段。要想知道第五个人岁数，需知道第四人的岁数，依次类推，推到第一人是10岁。这样再往回推。
答案：

def age(n):
    if n == 1: c = 10
    else: c = age(n - 1) + 2
    return c
print(age(5))

携程2016年面试题

输入一个不多于5位的正整数，要求：一、求它是几位数，二、逆序打印出各位数字。
答案：

a=int(input("请输入小于5位的数:"))
if len(str(a))>5:print("输入有误")
else:print("%s位数"%(len(str(a))),str(a)[::-1])

谷歌2014年算法题

题目:
有个8×8棋盘，其中对角的角落上，两个方格被切掉了。给定31块多米诺骨牌，一块骨牌恰好可以覆盖两个方格。用这31块骨牌能否盖住整个棋盘？请证明你的答案（提供范例，或证明为什么不可能）。

答案：
不能。
尝试用骨牌盖住第1行，而第1行只有7个方格，因此有一块骨牌必须铺至第2行。而用骨牌盖住第2行时，我们又必须将一块骨牌铺至第3行。
要盖住每一行，总有一块骨牌必须铺至下一行。无论尝试多少次、多少种方法，我们都无法成功铺下所有骨牌。
其实，还有更简洁更严谨的证明说明为什么不可能。棋盘原本有32个黑格和32个白格。将对角角落上的两个方格（相同颜色）切掉，棋盘只剩下30个同色的方格和32个另一种颜色的方格。为方便论证起见，我们假定棋盘上剩下30个黑格和32个白格。

放在棋盘上的每块骨牌必定会盖住一个白格和一个黑格。因此，31块骨牌正好盖住31个白格和31个黑格。然而，这个棋盘只有30个黑格和32个白格，所以，31块骨牌盖不住整个棋盘。

百度面试题

题目:
有5个海盗，按照等级从5到1排列，最大的海盗有权提议他们如何分享100枚金币。
但其他人要对此表决，如果多数反对，那他就会被杀死。
他应该提出怎样的方案，既让自己拿到尽可能多的金币又不会被杀死？
（提示：有一个海盗能拿到98%的金币）

答案：
从后向前推，如果1－3号强盗都喂了鲨鱼，只剩4号和5号的话，5号一定投反对票让4号喂鲨鱼，以独吞全部金币。所以，4号惟有支持3号才能保命。3号知道这一点，就会提（100，0，0）的分配方案，对4号、5号一毛不拔而将全部金币归为已有，因为他知道4号一无所获但还是会投赞成票，再加上自己一票，他的方案即可通过。不过，2号推知到3号的方案，就会提出（98，0，1，1）的方案，即放弃3号，而给予4号和5号各一枚金币。由于该方案对于4号和5号来说比在3号分配时更为有利，他们将支持他而不希望他出局而由3号来分配。这样，2号将拿走98枚金币。不过，2号的方案会被1号所洞悉，1号并将提出（97，0，1，2，0）或（97，0，1，0，2）的方案，即放弃2号，而给3号一枚金币，同时给4号（或5号）2枚金币。由于1号的这一方案对于3号和4号（或5号）来说，相比2号分配时更优，他们将投1号的赞成票，再加上1号自己的票，1号的方案可获通过，97枚金币可轻松落入囊中。这无疑是1号能够获取最大收益的方案了

华为2012算法题

题目:
有栋建筑物高100层。若从第N层或更高的楼层扔下来，鸡蛋就会破掉。若从第N层以下的楼层扔下来则不会破掉。给你2个鸡蛋，请找出N，并要求最差情况下扔鸡蛋的次数为最少。

答案：
我们发现，无论怎么扔鸡蛋1（Egg 1），鸡蛋2（Egg 2）都必须在“破掉那一层”和下一个不会破掉的最高楼层之间，逐层扔下楼（从最低的到最高的）。例如，若鸡蛋1从5层和10层楼扔下没破掉，但从15层扔下时破掉了，那么，在最差情况下，鸡蛋2必须尝试从11、12、13和14层扔下楼。
具体做法
首先，让我们试着从10层开始扔鸡蛋，然后是20层，等等。
如果鸡蛋1第一次扔下楼（10层）就破掉了，那么，最多需要扔10次。
如果鸡蛋1最后一次扔下楼（100层）才破掉，那么，最多要扔19次（10、20、…、90、100层，然后是91到99层）。
这么做也挺不错，但我们只考虑了绝对最差情况。我们应该进行“负载均衡”，让这两种情况下扔鸡蛋的次数更均匀。
我们的目标是设计一种扔鸡蛋的方法，使得扔鸡蛋1时，不论是在第一次还是最后一次扔下楼才破掉，次数越稳定越好。
(1) 完美负载均衡的方法应该是，扔鸡蛋1的次数加上扔鸡蛋2的次数，不论什么时候都一样，不管鸡蛋1是从哪层楼扔下时破掉的。
(2) 若有这种扔法，每次鸡蛋1多扔一次，鸡蛋2就可以少扔一次。
(3) 因此，每丢一次鸡蛋1，就应该减少鸡蛋2可能需要扔下楼的次数。例如，如果鸡蛋1先从20层往下扔，然后从30层扔下楼，此时鸡蛋2可能就要扔9次。若鸡蛋1再扔一次，我们必须让鸡蛋2扔下楼的次数降为8次。也就是说，我们必须让鸡蛋1从39层扔下楼。
(4) 由此可知，鸡蛋1必须从X层开始往下扔，然后再往上增加X1层……直至到达100层。
(5) 求解方程式X + (X1) + (X2) + … + 1 = 100，得到X (X + 1) / 2 = 100 → X = 14。
我们先从14层开始，然后是27层，接着是39层，依此类推，最差情况下鸡蛋要扔14次。

正如解决其他许多最大化/最小化的问题一样，这类问题的关键在于“平衡最差情况”。

拉勾网2014年面试题

题目:

1. 你首先说出三个不同的特殊数，要求必须是个位数，比如3、5、7。
2. 让所有学生拍成一队，然后按顺序报数。
3. 学生报数时，如果所报数字是第一个特殊数（3）的倍数，那么不能说该数字，而要说Fizz；如果所报数字是第二个特殊数（5）的倍数，那么要说Buzz；如果所报数字是第三个特殊数（7）的倍数，那么要说Whizz。
4. 学生报数时，如果所报数字同时是两个特殊数的倍数情况下，也要特殊处理，比如第一个特殊数和第二个特殊数的倍数，那么不能说该数字，而是要说FizzBuzz, 以此类推。如果同时是三个特殊数的倍数，那么要说FizzBuzzWhizz。
5. 学生报数时，如果所报数字包含了第一个特殊数，那么也不能说该数字，而是要说相应的单词，比如本例中第一个特殊数是3，那么要报13的同学应该说Fizz。如果数字中包含了第一个特殊数，那么忽略规则3和规则4，比如要报35的同学只报Fizz，不报BuzzWhizz。

现在，我们需要你完成一个程序来模拟这个游戏，它首先接受3个特殊数，然后输出100名学生应该报数的数或单词。

def check(a, dic, d):
    answer = ''
    if str(a) in str(d):
        return dic[a]
    for x in dic:
        if not (d % x):
            answer = answer + dic[x]
    if not answer:
        return d
    return answer
if __name__ == '__main__':
    a = int(input('input u a: '))
    b = int(input('input u b: '))
    c = int(input('input u c: '))
    dic = {a: 'Fizz', b: 'Buzz', c: 'Whizz'}
    for x in range(1, 101):
        print(check(a, dic, x))