leetcode第189题. 旋转数组----五种解法
目录
- 189. 旋转数组
- 解法一:暴力求解(依次旋转K轮)
- 解法二:额外空间法
- 解法三:三次翻转
- 解法四:环状替换
-
- 递归法
- 循环迭代法
189. 旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
进阶:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
解法一:暴力求解(依次旋转K轮)
思想:每次旋转一个数字,将其他N-1个数据依次挪动,K个数据就K次。(超时)
//方法一:暴力法(k次旋转法)---超时。
//---------------------------------
/*k=k%numsSize;
int temp=0;
for(int i=0;i0;j--)
{
nums[j]=nums[j-1];
}
nums[0]=temp;
}*/
//---------------------------------
解法二:额外空间法
思想: 申请额外k个空间arr,存放原数组 后k 个数据,再往右挪动原数组的数据k步,再将arr填充到 前n-k 个数据里。
//方法2:额外空间法
//申请额外k个空间arr,存放原数组 后k 个数据
//再往右挪动原数组的数据k步,再将arr填充到 前n-k 个数据里。
k=k%numsSize;
int *arr=(int *)malloc(k*sizeof(nums[0]));
if(arr!=NULL)
{
int Size=0;
for(int i=numsSize-k;i<numsSize;i++)
{
*(arr+Size)=nums[i];
Size++;
}
for(int j=numsSize-1-k;j>=0;j--)
{
nums[j+k]=nums[j];
}
for(int m=0;m<k;m++)
{
nums[m]=*(arr+m);
}
}
//可以申请好k个int的空间,然后用三次memcpy搞定。
解法三:三次翻转
思想:
第一次:将整个数组翻转逆置。
第二次:将前K个数据翻转逆置。
第三次:将后面一组n-k个数据翻转逆置。
void reverse(int *arr, int arrSize)
{
int temp = 0;
arrSize = arrSize - 1;
for (int i = 0; i < arrSize / 2 + arrSize % 2; i++)
{
temp = *(arr + arrSize - i);
*(arr + arrSize - i) = *(arr + i);
*(arr + i) = temp;
}
}
//方法四:三次反转
k=k%numsSize;
//第一次反转:整个数组反转。
reverse(nums,numsSize);
//第二次反转:反转k个数字。
reverse(nums,k);
//第三次反转:反转numsize-k个。
reverse(nums+k,numsSize-k);
解法四:环状替换
递归法
先看下面这种交换方式:
替换线指向的是对应数字,不是对应位置!!!
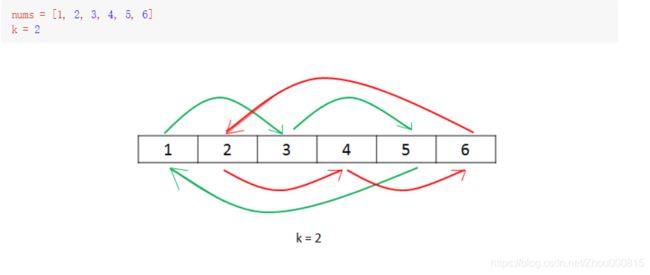
交换完成后,就是旋转2次的结果,5,6,1,2,3,4。
再来看下面这种:
//方法三:环状替换
//递归法
//-------------------------------------------------
k=k%numsSize;
if(k==0)
{
return ;
}
int times=0;
while(times<k)
{
for(int i=times;i<numsSize;i+=k)
{
if(i+k<numsSize)
{
swap(&nums[times],&nums[i+k]);
}
else
{
break;
}
}
times++;
}
int nextk=0;
if(numsSize%k==0)
{
return;
}
else
{
nextk=k-numsSize%k;
rotate(nums,k,nextk);
}
//-------------------------------------------------
循环迭代法
递归法是先旋转,消除余数。
而循环迭代法,我们直接求n和k的最大公约数count,分count组,直接消除余数的存在,最后一个替换数字的下一个(会数组越界,取余数拿到正确的数组下标)就是该组的起始位置,首尾相接,一个组的替换完成退出。
外面再讨厌一个循环,控制组数。
图解:

代码:
void swap(int *num1,int *num2)
{
int temp=*num1;
*num1=*num2;
*num2=temp;
}
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
//循环迭代法
//-------------------------------------------------
k=k%numsSize;
if(k==0)
{
return ;
}
int count=gcd(numsSize,k);
int group=0;
while(group<count)
{
for(int i=group+k;1;i+=k) //group下标是每组的第一个下标,用第一个位置保存下一个数据,不必再开单独的空间。i+group则是要交换的位置下标
{
if(i%numsSize!=group)
{
swap(&nums[group],&nums[i%numsSize]);
}
else
{
break;
}
}
group++;
}
//-------------------------------------------------
