Codeforces Round #700 (Div. 2)全部题解

题目链接：https://codeforces.com/contest/1480

---

A.Yet Another String Game

贪心
题目大意为给定若干个字符串，Alice和Bob轮流对字符串每一位进行改变操作，每一位只能被改变一次，Alice先手，Alice要使字符串字典序尽可能小，Bob要使字符串字典序尽可能大，求最后结果。
贪心策略，一定是优先更改靠前的字符，Alice回合，若当前字符不为最小，则将其改为最小’a’，否则将其改为’b’，Bob同理，若当前字符不为最大，则将其改为最大’z’，否则将其改为’y’。

#include
#define ll long long
#define next next_
#define y1 yy
using namespace std;
int _,len;
string s;
int main(){
     
	scanf("%d",&_);
	while(_--){
     
		cin>>s;
		len=s.size();
		for(int i=0;i<len;i++){
     
			if(i&1){
     
				if(s[i]=='z') s[i]='y';
				else s[i]='z';
			}
			else{
     
				if(s[i]=='a') s[i]='b';
				else s[i]='a';
			}
		}
		cout<<s<<'\n';
	}
	return 0;
}

B.The Great Hero

排序，数学
题意要求判断对于给定的所有怪物与英雄的攻击力和血量，判断英雄能否击败所有怪物（包括同归于尽）。
先对所有怪物按照攻击力升序进行排序（攻击力大的怪物放在最后，可以与其同归于尽），再分别算出击败每个怪物所需的攻击次数，并再整个过程中扣除英雄相应的血量，最后一只怪物特判能否与其同归于尽。

#include
#define ll long long
#define next next_
#define y1 yy
using namespace std;
ll _,A,B,n;
struct p{
     
	ll a;
	ll b;
}a[100010];
bool cmp(p x,p y){
     
	if(x.a!=y.a) return x.a<y.a;
	return x.b<y.b;
}
int main(){
     
	scanf("%lld",&_);
	while(_--){
     
		bool ok=true;
		scanf("%lld%lld%lld",&A,&B,&n);
		for(ll i=1;i<=n;i++) scanf("%lld",&a[i].a);
		for(ll i=1;i<=n;i++) scanf("%lld",&a[i].b);
		sort(a+1,a+1+n,cmp);
		for(ll i=1;i<=n;i++){
     
			if(i==n){
     
				ll num1=B/a[i].a+(B%a[i].a!=0),num2=a[i].b/A+(a[i].b%A!=0);
				if(num1<num2) ok=false;
				break;
			}
			ll num=a[i].b/A+(a[i].b%A!=0);
			B-=num*a[i].a;
			if(B<=0){
     
				ok=false;
				break;
			}
		}
		if(ok) printf("YES\n");
		else printf("NO\n");
	}
	return 0;
}

C.Searching Local Minimum

二分，交互
题意为给出一个排列的长度，每次你可以询问得到一个下标元素的值，要求在100次询问内找出满足a[i] 二分查找即可，对于每次查找的mid，求出a[mid],a[mid-1],a[mid+1]并判断a[mid],a[mid-1],a[mid+1]是否满足条件，满足则输出，若不满足，若a[mid]>a[mid-1]，则更新r=mid-1，反之则更新l=mid+1。
这里可以理解为二分查找一直往元素小的方向走，假设a[mid]>a[mid-1]，若[l,mid-2]区间内元素都比a[mid]大，则mid即为答案，若[l,mid-2]区间内元素都比a[mid]小，且为严格升序，则答案在边界的位置，否则在区间中间一定存在a[i]

#include
#define ll long long
#define next next_
#define y1 yy
int n,a[100010];
int q(int t){
     
	printf("? %d\n",t);
	fflush(stdout);
	int x;
	scanf("%d",&x);
	return x;
}
int main(){
     
	scanf("%d",&n);
	if(n==1) return printf("! 1"),0;
	int l=1,r=n;
	while(l<=r){
     
		int mid=l+r>>1;
		if(!a[mid]) a[mid]=q(mid);
		if(mid-1>=1&&!a[mid-1]) a[mid-1]=q(mid-1);
		if(mid+1<=n&&!a[mid+1]) a[mid+1]=q(mid+1);
		if(mid==1){
     
			if(a[mid]<a[mid+1]) return printf("! %d",mid),0;
			else l=mid+1;
		}
		else if(mid==n){
     
			if(a[mid]<a[mid-1]) return printf("! %d",mid),0;
			else r=mid-1;
		}
		else{
     
			if(a[mid]<a[mid-1]&&a[mid]<a[mid+1]) return printf("! %d",mid),0;
			else{
     
				if(a[mid]>a[mid-1]) r=mid-1;
				else l=mid+1;
			}
		}
	}
	return 0;
}

D1.Painting the Array I

贪心
题意为给定一个数列，要求将其分为2个子序列，并将子序列中相邻且相同的元素合并，求最后两个子序列中的元素个数之和的最大值。
用a，b表示两个子序列中的最后一个元素的位置下标，pos[i]表示下标为i的元素之后离它最近的与它相同的元素位置。
遍历数列中的元素，若当前数与两个序列中的最后一个数都相同，则只能将其合并，并将pos[c[i]]尾元素弹出，若两个子序列末尾数有一与当前数相同，则将当前数压入末尾数不同的序列中，并更新下标，若两个子序列末尾数都与当前数不同，则比较与两个序列末尾数相同的下一个数的距离，若a序列末尾数的下一个数的距离比b序列近，则对接下来结果影响较大的是a序列末尾数，则将当前数压入序列a中，因为要使长度尽量长，要尽量避免相同的两个数相邻，反之，则将当前数压入b序列中，最后将pos[c[i]]尾元素弹出。
最后统计数的个数。

#include
#define ll long long
#define next next_
#define y1 yy
using namespace std;
vector<int> pos[100010];
int n,c[100010],next[100010],a,b,ans;
int main(){
     
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&c[i]);
	for(int i=n;i>=1;i--)
		pos[c[i]].push_back(i);
	for(int i=1;i<=n;i++){
     
		if(c[a]==c[i]){
     
			if(c[b]!=c[i]){
     
				ans++;
				b=i;
			}
			pos[c[i]].pop_back();
		}
		else if(c[b]==c[i]){
     
			if(c[a]!=c[i]){
     
				ans++;
				a=i;
			}
			pos[c[i]].pop_back();
		}
		else{
     
			if(!pos[c[a]].size()){
     
				ans++;
				b=i;
			}
			else if(!pos[c[b]].size()){
     
				ans++;
				a=i;
			}
			else if(pos[c[a]].back()<pos[c[b]].back()){
     
				ans++;
				a=i;
			}
			else{
     
				ans++;
				b=i;
			}
			pos[c[i]].pop_back();
		}
	}
	cout<<ans;
	return 0;
}

D2.Painting the Array II

贪心
题意与D1相同，只是改为求最小值。
遍历一遍输入数列，若当前两个序列有一末尾数与当前数相同，则直接合并，若都不相同，则比较与两个序列末尾数相同的下一个数的距离，若a序列末尾数的下一个数的距离比b序列近，则将当前数压入b中，因为要使长度尽量短，要尽量使得相同的两个数相邻，反之，则将当前数压入a序列中，最后将pos[c[i]]尾元素弹出。
最后统计数的个数。

#include
#define ll long long
#define next next_
#define y1 yy
using namespace std;
vector<int> pos[100010];
int n,c[100010],next[100010],a,b,ans;
int main(){
     
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&c[i]);
	for(int i=n;i>=1;i--)
		pos[c[i]].push_back(i);
	for(int i=1;i<=n;i++){
     
		if(c[a]==c[i]||c[b]==c[i]) pos[c[i]].pop_back();
		else{
     
			if(!pos[c[a]].size()){
     
				ans++;
				a=i;
			}
			else if(!pos[c[b]].size()){
     
				ans++;
				b=i;
			}
			else if(pos[c[a]].back()>pos[c[b]].back()){
     
				ans++;
				a=i;
			}
			else{
     
				ans++;
				b=i;
			}
			pos[c[i]].pop_back();
		}
	}
	cout<<ans;
	return 0;
}

E.Continuous City

二进制，图论
题意为给你一个区间[l,r]，要求你构造一个有向图，图中的边只能从序号小的点指向序号大的点，并且图中从节点1到达节点n的所有路径中，路径的长度恰好分布在区间[l,r]中且每种长度出现且仅出现一次。
在解决多重背包问题时曾经运用到又给二进制优化的方法，即将相同的物品个数拆分成若干个二的整数次幂的和的形式，这里也自然会想到二进制拆分，但因为要求每种长度出现且仅出现一次，所以有一点变化。
首先特判l=r的情况。
考虑l=1的情况，若不考虑r，初始时放置2个点①，②，从①到②建立一条权值为1的边，此时图中覆盖了区间[1,1]内的所有值。

继续加入点③，并建立一条从①到③的边，权值为1，再建立一条从②到③的边，权值为2，这时我们从1①出发，依照三条路径经过②和③分别能得到1，2，3，此时图中覆盖了区间[1,3]内的所有值。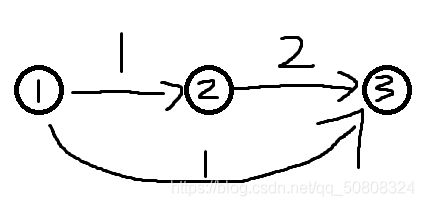
如此往复加点，最终我们从①出发经过图中的每个点时能分别得到区间[1,2ⁿ-1]中的所有值。

此时我们再从每个点上都引出一条指向终点的边，便可得到区间[1,2ⁿ]中的所有值。

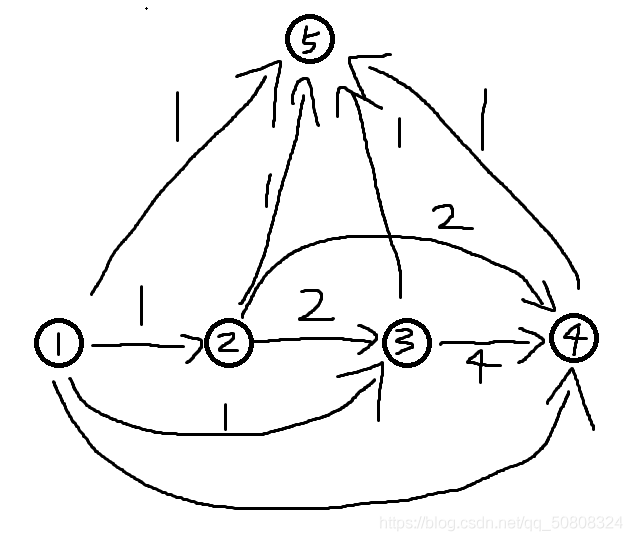
但这仅仅只是r为2的整数次幂的情况下，若r不为2的整数次幂，这种情况就行不通，而我们想到可以通过2的整数次幂来表示一个连续区间内的所有值，那么对这个区间边界进行加减，就可以表示出其余的区间，于是自然想到将一个能够表示区间[1,2ⁱ]的子图末尾接上一条特定权值的边再连向终点。但上图的表示方式仅仅是在特定的点上能够表示出特定的几个值，我们需要构造一个图，使其从①开始，经过中间的点最后到达终点时能够表示出区间[1,2ⁱ]的所有值，如下图。

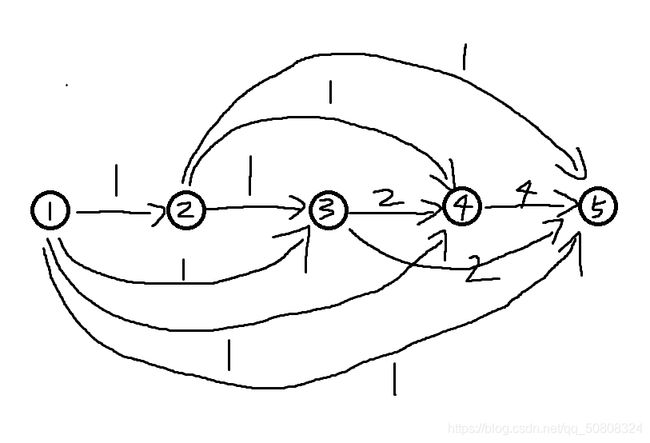
只要从①出发，经过中间若干个点，最后到达⑤的所有路径长度中完全覆盖了区间[1,2³]内的所有数。此时再从⑤在引出一条边，即可起到区间平移的作用。
那么最终的策略已经出来了，找出比r小且离r最近的2ⁿ，先仿照上图构造出一个能够表示区间[1,2ⁿ]内所有数的图，再将r减去2ⁿ，多出来的一部分区间利用从中间点引出新边来产生。
以上图为例若l=1，r=11，在点⑤的右侧添加一条权值为1的边，指向点⑥，同时从点①引出一条权值为1的边，指向点⑥，此时图中表示出了区间[1,2³+1]内的所有数，此时r-9=2，2即为2¹，所以从点②引出一条权值为9的边连接到点⑥上即可。

#include
#define ll long long
#define next next_
#define y1 yy
using namespace std;
vector<tuple<ll,ll,ll> >app;
ll l,r,maxn,sum,wn,pos;
void work(ll l,ll r){
     
	ll num=1;
	maxn=1;
	while(num*2<=r) num<<=1,maxn++;
	maxn++;
	for(ll i=1;i<=maxn;i++)
		for(ll j=i+1;j<=maxn;j++) app.push_back({
     i,j,max(1ll,1ll<<(i-2))});
	sum=num;
	if(sum==r) return;
	else{
     
		maxn++;
		app.push_back({
     1,maxn,1ll});
		app.push_back({
     maxn-1,maxn,1ll});
		sum++;
		while(sum<r){
     
			num=1;
			pos=1;
			while(num*2<=r-sum) num<<=1,pos++;
			pos++;
			app.push_back({
     pos,maxn,sum});
			sum+=num;
		}
	}
}
int main(){
     
	scanf("%lld%lld",&l,&r);
	if(l==r) return printf("YES\n%lld %lld\n%lld %lld %lld",2ll,1ll,1ll,2ll,l),0;
	wn=l-1;
	l-=wn;
	r-=wn;
	work(l,r);
	if(wn) app.push_back({
     maxn,maxn+1,wn}),maxn++;
	printf("YES\n%lld %lld\n",maxn,(ll)app.size());
	for(auto [x,y,z]:app) printf("%lld %lld %lld\n",x,y,z);
	return 0;
}