C#实现字符串匹配算法
最近在学习算法。刚学习完字符串匹配的几种算法:BF算法、MP算法:KMP算法,BM算法和BMH算法。参考的书籍是算法之美,原书的代码都是用C++写的。我不懂C++,只学过C#,这里就用C#做个总结(自己是个菜鸟,表达错误的地方,希望大家指正)。
1、BF算法
BF算法实现原理是:从主串和模式串的首位置开始,依次比较主串和模式串的各个位置,如果匹配错误,主串就返回第二个位置,模式串返回首位置,重新匹配。以此类推,直到模式串匹配成功,返回匹配成功的位置。如果没有发生匹配就返回-1。
代码如下:
public static int MatchStr(string s1, string s2,int n)
{
int i = n-1, j = 0; //n为匹配的起始位置
bool IsMatch=false ;
while (!IsMatch)
{
if (s1[i] == s2[j])
{
i++;
j++;
}
else
{
i = i - j + 1;
j = 0;
}
//如果模式串匹配成功,j++,就会得到模式串长度的值。
if (j == s2.Length)
{
IsMatch = true;
n = i - j+1;
}
}
if (IsMatch)
{
Console.WriteLine("普通方法匹配成功");
}
else
{
n = -1;
Console.WriteLine("普通方法匹配失败");
}
return n;
}
2、MP算法
BF算法一旦匹配失败,i,j的值就会频繁的回溯,导致复杂度增大。MP算法避免的i值回溯,只利用j值的回溯进行匹配。
MP算法原理:模式串与主串进行匹配,进行到i处(模式串在j处)发现不匹配,如果模式串j处之前有前缀n个字符与主串i处
之前n个字符相匹配,则可将模式串j移动到n处,重新与i进行匹配(此时i的位置不变)即可。依次类推,直到匹配结束。
现在的问题就是求n的值为多少。
假设模式串与主串在i处不匹配(模式串在j处),那么说明主串的s1[i-j~i-1]的子串与模式串的s2[0~j-1]是匹配成功的。那么寻找
主串i之前的n个字符,等价于寻找模式串j之前的n个字符与模式串的前缀n个字符是相匹配的,即n的值与主串无关,只与模式串自
身的j位置有关。n的计算方法计算如下:假定模式串为(ababcabababc)
{
int[] next = new int[s1.Length + 1]; //数组的长度可以为s1.length,这里为s1.length+1,在多次匹配中才有意义。
int i = 1, j = 0;
next[0] = -1;
next[1] = 0;
while (i < s1.Length)
{
if (j==-1||s1[i] == s1[j]) //j==-1的条件是为了避免i=0时候,next[0]=-1,造成的下标越界
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j];
}
}
return next;
}
{
int[] next = MpNext(s2);
int i = n - 1,j = 0;
bool IsMatch = false ;
while (!IsMatch)
{
if (j == -1 || s1[i] == s2[j])
{
i++;
j++;
}
else
{
j = next[j];
}
if (j == s2.Length)
{
IsMatch = true;
n = i - j + 1;
}
}
if (IsMatch)
{
Console.WriteLine("MP方法匹配成功");
}
else
{
n = -1;
Console.WriteLine("MP方法匹配失败");
}
return n;
}
{
int[] next = new int[s1.Length + 1];
int i = 1, j = 0;
next[0] = -1;
next[1] = 0;
while (i < s1.Length)
{
if (j == -1 || s1[i] == s1[j])
{
i++;
j++;
if (i < s1.Length && s1[i] == s1[j])
{
next[i] = next[j];
}
else
{
next[i] = j;
}
}
else
{
j = next[j];
}
}
return next;
}
{
int[] bmBc = new int[256]; //这里为ASCII码中的256个字符,因为不能预知模式串中的字符
for (int i = 0; i < bmBc .Length ; i++)
{
bmBc[i] = s1.Length; //首先把所有值赋值为模式串的长度。
}
for (int i = 0; i < s1.Length-1 ; i++)
{
bmBc[s1[i]] = s1.Length - i -1; //依次计算模式串中字符的bmBc值。
}
return bmBc;
}
{
int[] bmGs = new int[s1.Length] ;
for (int i = s1.Length -1; i > 0; i--)
{
for (int s = i - 1; s >= 0; s--) //对于第一种情况,s代表出现好后缀的位置
{
if (s1[s] != s1[i]) //s1[i]处与主串是不匹配的,所以要找与s1[i]不同的值
{
if (i ==s1.Length - 1) //此时是末尾第一个字符就不匹配
{
bmGs[i] = i - s;
}
for (int k = i+1; k
if (s1[k - i + s] != s1[k]) break; /
else
{
if (k ==( s1.Length - 1)) //好后缀匹配成功
{
bmGs [i] =i - s;
}
}
}
}
if (bmGs[i] > 0) break; //表示已经取得了一个好后缀的最小移动位置,就不用继续循环了
}
if (bmGs[i] == 0) //对应于第二种情况。第二种情况是第一种情况失败后开始的
{
for (int k = Math.Min(s1.Length - 1 - i, i); k > 0; k--) //k代表好后缀长度,好后缀一定比 s1.Length-1-i、i都小
{
int x = s1.Length - 1, y = k - 1; //x,表示模式串尾部。
while (s1[x] == s1[y])
{
if (y == 0) //好后缀匹配成功
{
bmGs[i] = s1.Length - k;
break;
}
x--;
y--;
}
}
if (bmGs[i] == 0) //代表第三种情况。一二种情况都没出现。
{
bmGs[i] = s1.Length;
}
}
}
return bmGs;
}
{
int[] bmBc = BmbmBc(s2);
int[] bmGs = BmbmGs(s2);
int x=n+s2.Length -2;
int y=s2.Length -1;
bool IsMatch = false;
while (!IsMatch)
{
if (s1[x] == s2[y])
{
if (y == 0)
{
IsMatch = true;
n = x+1;
}
x--;
y--;
}
else
{
int offset = Math.Max(bmBc[s1[x]], bmGs[y]); //偏移的最大值
x += offset;
y = s2.Length - 1;
}
}
if (IsMatch)
{
Console.WriteLine("BM方法匹配成功");
}
else
{
n = -1;
Console.WriteLine("BM方法匹配失败");
}
return n;
}
{
string s1 = "GCATCGCAGAGAGTATACAGTACG";
string s2 = "GCAGAGAG";
int n = Program.MatchStr(s1, s2, 1);
Console.WriteLine("普通方法匹配的位置为:" + n);
int m = Program.MpMatchStr(s1, s2, 1);
Console.WriteLine("MP方法匹配的位置为:" + m);
int x = Program.MpMatchStr(s1, s2, 1);
Console.WriteLine("KMP方法匹配的位置为:" + x);
int y = Program.BmMatchStr(s1, s2, 1);
Console.WriteLine("BM方法匹配的位置为:" + y);
}
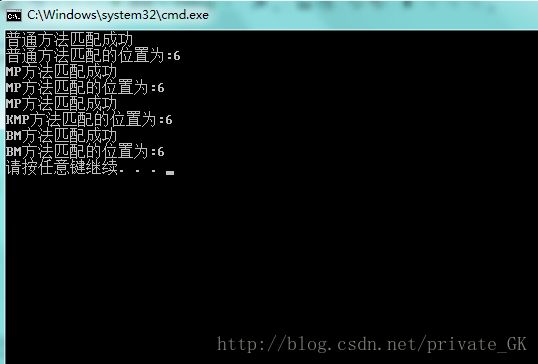
结果如下: