神经网络学习笔记(一)——卷积神经网络CNN

卷积神经网络 CNN

一、概述

  卷积神经网络（Convolutional Neural Network, CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。
  卷积神经网络由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。

二、卷积的概念

  微积分中卷积的表达式为：
$$S(t)=\int x(t-a)w(a)da$$
  离散形式表示为：
$$s(t)=\sum _{a}x(t-a)w(a)$$
  用矩阵形式可以表示为：
$$s(t)=(X\ast W)(t),\ast 表示卷积$$
  二维的卷积表达式为：
$$s(i,j)=(X\ast W)(i,j)=\sum _m\sum _{n}x(i-m,j-n)w(m,n)$$
  在CNN中，二维卷积形式与上式稍有差别，表达为：
$$s(i,j)=(X\ast W)(i,j)=\sum _m\sum _{n}x(i+m,j+n)w(m,n)$$

  其中，$W$为卷积核，而X则为输入。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵；如果X是多维张量，那么W也是一个多维的张量。

三、CNN原理

  CNN有三个基本思想，局部感受野(local receptive fields)、权值共享(shared weights)、池化(pooling)。

3.1 卷积层

  卷积层是一组平行的特征图（feature map），它通过在输入矩阵上滑动不同的卷积核并运行一定的运算而组成。卷积核的尺寸要比输入矩阵小得多，且重叠或平行地作用于输入图矩阵，一张特征图中的所有元素都是通过一个卷积核计算得出的，也即一张特征图共享了相同的权重和偏置项。局部感受野和权值共享都在这一层进行实现。

  如下图所示，输入是一个二维的$3\times 4$的矩阵，而卷积核是一个$2\times 2$的矩阵。假设卷积是一次移动一个像素来卷积的，对输入的左上角$2\times 2$的局部和卷积核卷积，得到的输出矩阵$S$的$S_{00}$的元素为$aw+bx+ey+fz$。同样的方法以得到输出矩阵的其它元素。

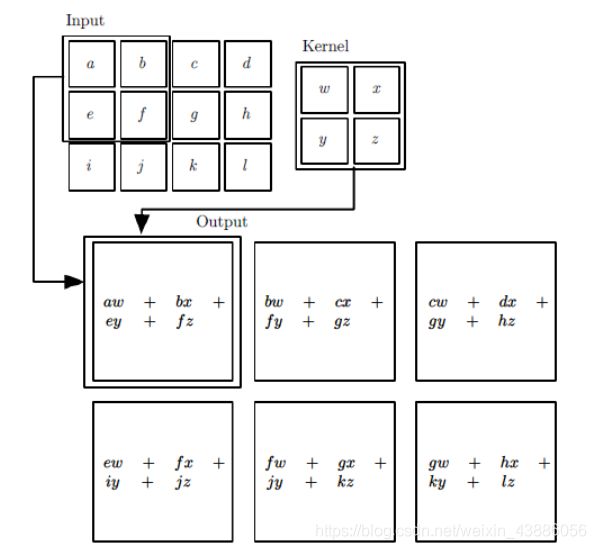
  对于多维输入的卷积，应当对各个子矩阵分别进行卷积求和之后再加上偏置$b$：
$$s(i,j)=(X\ast W)(i,j)+b=\sum _{k=1}^n(X_k\ast W_k)(i,j)+b$$

  激活函数

  常用的激活函数有sigmoid（$f(x)=\frac{1}{1+e^{-z}}$）、tanh（$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$）、relu（$f(z)=\max (0,x)$）等等，前两者sigmoid/tanh比较常见于全连接层，后者relu常见于卷积层。ReLU函数更受青睐可以将神经网络的训练速度提升数倍，而并不会对模型的泛化准确度造成显著影响。

  线性整流子层
  线性整流子层（Rectified Linear Units layer, ReLU layer）使用线性整流ReLU：$f(x)=\max (0,x)$ 作为这一层神经的激励函数。它可以增强判定函数和整个神经网络的非线性特性，而本身并不会改变卷积层。ReLU的优点是收敛快，求梯度简单。

  权值共享

$$\sigma (b+\sum _{m=0}^M\sum _{n=0}^N{w}_{m,n}{a}_{i+m,j+n})$$
  $\sigma$是激活函数，如sigmoid函数，ReLU函数等，b是偏移值，w是共享权值矩阵。
$$a^1=\sigma (b+w\ast a^0)$$
  $a^1$表示隐藏层的输出，$a^0$表示隐藏层的输入，而∗就表示卷积操作。

  由于权值共享，卷积核相同，从而第一个隐藏层所有的神经元从输入层探测到的是同一种特征，只是探测到的位置不同。如果想要学习更多的特征，就需要更多的窗口，即使用多个卷积核。卷积核之间的w和b是不共享的，从而能够从输入层的各个位置学到多种不同的特征。
  权值共享减少重复的卷积核，可以大大减少模型参数的个数。

3.2 池化层

  池化（Pooling）是卷积神经网络中另一个重要的概念，实际上是一种非线性形式的降采样。有多种不同形式的非线性池化函数，而其中“最大池化（Max pooling）”是最为常见的。它是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。

  这种机制能够有效地原因在于，一个特征的精确位置远不及它相对于其他特征的粗略位置重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。

  池化层每次在一个池化窗口（depth slice）上计算输出，然后根据步幅移动池化窗口。目前最常用的池化层，步幅为2，池化窗口为 $2\times 2$的二维最大池化层。每隔2个元素从图像划分出 $2\times 2$的区块，然后对每个区块中的4个数取最大值。这将会减少75%的数据量。

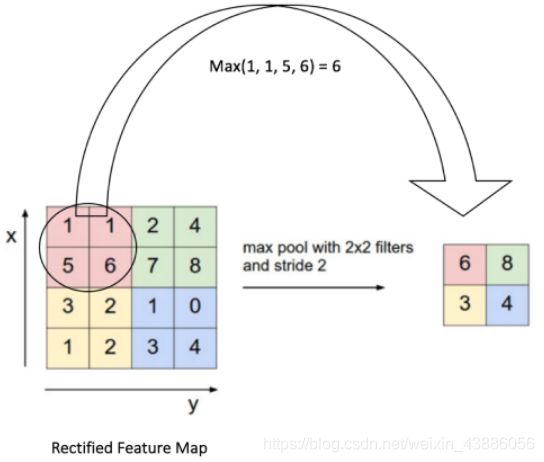
  除了最大池化之外，池化层也可以使用其他池化函数，例如“平均池化”，“L2-范数池化”（池化窗口扫过的区域里所有神经元平方后求和再开根号）等。

3.3 完全连接层

  最后，在经过几个卷积和最大池化层之后，神经网络中的高级推理通过完全连接层来完成。就和常规的非卷积人工神经网络中一样，完全连接层中的神经元与前一层中的所有激活都有联系。因此，它们的激活可以作为仿射变换来计算，也就是先乘以一个矩阵然后加上一个偏差(bias)偏移量。

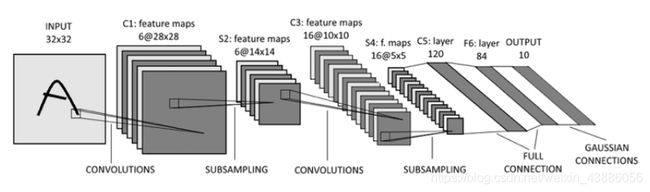
  典型的CNN并是多层结构，例如LeNet-5的结构就如下图所示：

  卷积层 – 池化层- 卷积层 – 池化层 – 卷积层 – 全连接层

3.4 权值矩阵BP算法

• $a^l$ :第$l$层神经元的输出
• $z^l$:第$l$层神经元的输入
• $W^l$:从$l-1$层mapping到$l$层权值矩阵
• $b^l$:与上面参数对应的偏移值
• $x$:train data的输入
• $y$:train data正确的label

  假设输出层为第L层，利用均方差来标定损失，对应损失函数如下：
$$J(W,b,x,y)=\frac{1}{2}||a_L-y|{|}_2^2$$

  卷积的正向传播公式如下：
$$\{\begin{array}{l}{a}^l=\sigma (z^l)=\sigma (a^{l-1}\ast W^l+b^l)\\ z^l=a^{l-1}\ast W^l+b^l=\sigma (z^{l-1})\ast W^l+b^l\end{array}$$

  带入损失函数，得到
$$J(W,b,x,y)=\frac{1}{2}||a_L-y|{|}_2^2=\frac{1}{2}||\sigma (a^{L-1}\ast W^L+b^L)-y|{|}_2^2$$

  将上式对W，b求梯度，令${\delta }^l=\frac{\partial J(W,b,x,y)}{\partial z^l}$

  得到传递公式如下：
$${\delta }^{l-1}={\delta }^l\frac{\partial z^l}{\partial z^{l-1}}={\delta }^l\ast rot180(W^l)\odot {\sigma }^{\prime }(z^{l-1})$$

  从而利用卷积求导推出
$$\frac{\partial J(W,b)}{\partial W^l}=\frac{\partial J(W,b)}{\partial z^l}\frac{\partial z^l}{\partial W^l}={\delta }^l\ast rot180(a^{l-1})$$

  而对于池化层，前向传播时池化层一般的操作是MAX或Average等，因此要从压缩过的误差${\delta }^l$来还原一个较大区域的误差：unsample。其具体操作是把所有子矩阵各个池化局部的值放在之前做前向传播时所作贡献的位置。
  以Max-Pooling为例，若${\delta }^l$的第k个子矩阵为${\delta }_k^l=\left(\begin{array}{cc}1& 5\\ 3& 7\end{array}\right)$，池化窗口大小为$2\times 2$，且前向传播时记录的最大值的位置分别是左上，左下，右下，右上，unsample还原后的矩阵为：
$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 5& 0\\ 0& 0& 0& 7\\ 0& 3& 0& 0\end{array}\right)$$

  由于池化层是对卷积层的输出做池化，因此求$\delta$的公式为：
$${\delta }_k^{l-1}=\frac{\partial J(W,b)}{\partial a_k^{l-1}}\frac{\partial a_k^{l-1}}{\partial z_k^{l-1}}=unsample({\delta }_k^l)\odot {\sigma }^{\prime }(z_k^{l-1})$$

3.5 层的尺寸设置

• 输入层：一般采用2的高次幂。
• 卷积层：使用小尺寸滤波器（比如3x3或最多5x5），使用步长S=1。还有一点非常重要
• 池化层：常用的设置是用2x2的最大值汇聚，步长为2（S=2）。注意这一操作将会把输入数据中75%的激活数据丢弃。不太常用的设置是使用3x3的矩阵，步长为2。最大值汇聚的感受野尺寸很少超过3，因为汇聚操作过于激烈，易造成数据信息丢失，会导致算法性能变差。

四、CNN简单使用

  在自然语言处理中，使用CNN进行文本分类可以取得不错的效果。将每个单词作为一个特征向量，使用了二维的卷积核进行Filter。利用CNN模型对语料进行了文本分类的处理。

  首先从文件中读取相应训练集和测试集的语料，利用jieba对文本进行分词，然后利用nltk去停用词。这里nltk_data中并没有中文的停用词，我从网上找了一个中文的停用词文件放在对应的stopwords目录下，并命名为chinese。

def tokenizer(text):
    sentence = jieba.lcut(text, cut_all=False)
    stopwords = stopwords.words('chinese')
    sentence = [_ for _ in sentence if _ not in stopwords]
    return sentence

  利用torchtext包处理预处理好的语料，将所提供的语料集转化为相应的词向量模型。由于每一个词均为一个向量，即一维矩阵，多个词便可以拼接成为二维矩阵，作为CNN的输入。

train_set, validation_set = data.TabularDataset.splits(
            path='corpus_data/',
            skip_header=True,
            train='corpus_train.csv',
            validation='validation.csv',
            format='csv',
            fields=[('label', label), ('text', text)],
        )
text.build_vocab(train_set, validation_set)

  将处理好的词向量输入到CNN模型中进行处理。

def forward(self, x):
    # 输入x的维度为(batch_size, max_len)
    x = self.embedding(x) # 经过embedding,x的维度为(batch_size, max_len, embedding_dim)
    x = x.view(x.size(0), 1, x.size(1), self.args.embedding_dim)

    # 经过卷积运算, x中每个运算结果维度为(batch_size, out_chanel, w, h=1)
    x = [F.relu(conv(x)) for conv in self.convs]
    # 经过最大池化层, 维度变为(batch_size, out_chanel, w=1, h=1)
    x = [F.max_pool2d(input=x_item, kernel_size=(x_item.size(2), x_item.size(3))) for x_item in x]
    # 将卷积核运算结果维度（batch，out_chanel,w,h=1）展平为（batch, outchanel*w*h）
    x = [x_item.view(x_item.size(0), -1) for x_item in x]
    # 将不同卷积核提取的特征组合起来
    x = torch.cat(x, 1)
    # dropout层
    x = self.dropout(x)
    # 全连接层
    out = self.linear(x)
    return out

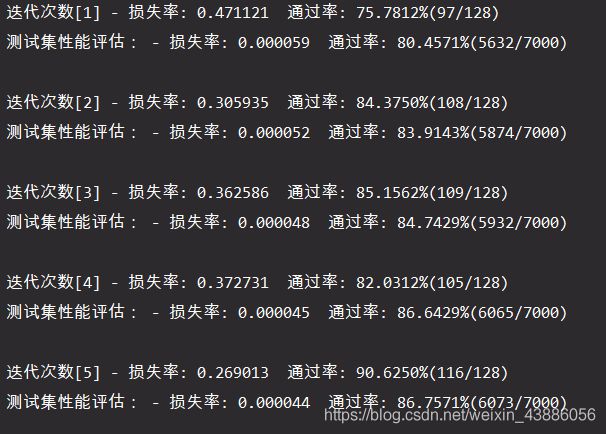
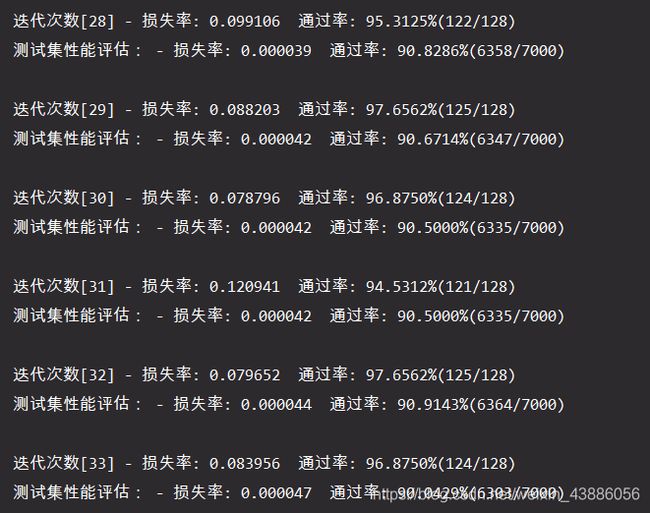
  利用训练集对模型进行训练，同时评估训练效果，并利用测试集对模型的准确性进行评估。为了防止偶然性产生的不确定，每一轮迭代会产生100个模型，分别评估其效率，进行调优后再用测试集测试其效率。

  在训练初期，准确率大概在80%左右。

  多轮迭代之后，模型的准确率可以达到90%以上。

五、总结

• CNN的核心思想
  • 局部感知(local field)，
  • 权值共享(Shared Weights)
  • 池化(Pooling)
• CNN的基本原理：
  • 卷积层：保留输入特征
  • 池化层：降维，防止过拟合
  • 全连接层：根据不同任务输出结果
• CNN的价值：
  • 将大数据量的输入有效的降维成小数据量，并不影响结果
  • 能够保留输入的特征，类似人类的视觉原理
• CNN的实际应用
  • 图片分类、检索
  • 目标定位检测
  • 人脸识别
  • 文本分类