word2vec 原理（二）基于 Hierarchical Softmax 的模型

1. negative sampling and hierarchical softmax

由于softmax运算考虑了背景词可能是词典 V 中的任一词，以上损失包含了词典大小数目的项的累加。在上一节中我们看到，不论是skip-gram模型还是cbow模型，由于条件概率使用了softmax运算，每一步的梯度计算都包含词典大小数目的项的累加。对于含几十万或上百万词的较大词典，每次的梯度计算开销可能过大。为了降低该计算复杂度，提出了2种优化，即负采样（negative sampling）或层序softmax（hierarchical softmax），这一节，将主要讲解基于 Hierarchical Softmax 的cbow和skip-gram模型

2. CBOW model

2.1 原理图

cbow是在已知当前中心词$w_t$的上下文$w_{t-2},w_{t-1},w_{t+1},w_{t+2}$的情况下来预测当前词$w_t$。
图为cbow的网络结构：

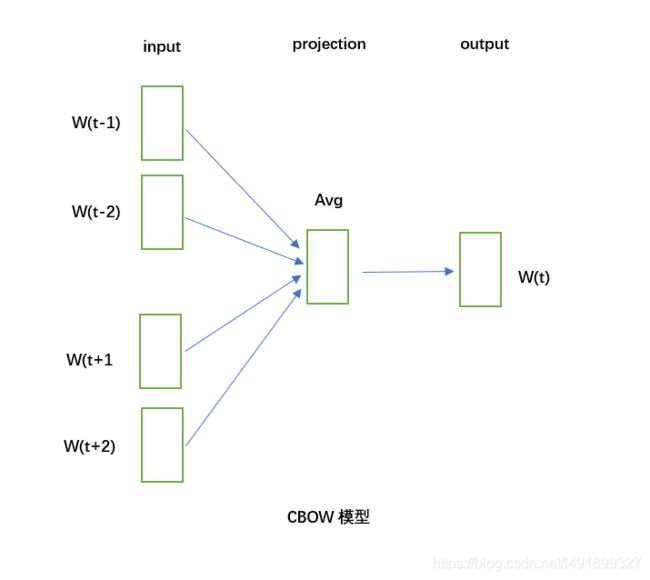
可以看到，cbow分为输入层，隐藏层和输出层，以（contenxt(w),w）为例，其中context(w)包含w的上下文，假设窗口长度为c,则context(w)包含了w前c个词和后c个词的词向量。
这里将对输入、隐藏、输出层做出解释：
输入层：context(w)，由于包含2c个向量，此处假设context(w) = ($v_1,v_2,...,v_c,v_{c+1},...,v_{2c}，v\in {\mathbb{R}}^m$，此处m为词向量长度)
隐藏层:将输入层的2c个向量作求和平均,$x_w=\frac{{\sum }_{i=1}^{2c}{v}_i}{2c},x_w\in {\mathbb{R}}^m$

输出层：一棵Huffman树,它是以语料库中出现过的词作为叶子节点，词的出现次数作为叶子节点的权重。在huffman树中，叶子节点个数$N=|D|$,分别对应词典D中的词，非叶子节点数为$|D-1|$

2.2 梯度计算

2.2.1 参数

Hierarchical Softmax是word2vec中用于提高性能的一项关键技术。为了描述方便，引入若干符号。考虑到Huffman树种的某个叶子结点，假设对应词典D中的词w，记

1. $p^w$:从根结点出发到达w对应的叶子结点的路劲。
2. $l^w$：路径$p^w$中包含结点的个数。
3. $p_1^w,p_2^w,...,p_{l^w}^w$:路径$p^w$中的$l^w$个结点，其中$p_1^w$表示根结点，$p_{l^w}^w$表示词$w$对应的结点。
4. $d_1^w,d_2^w,...,d_{l^w}^w\in [0,1]$:词$w$的Huffman编码，它由$l^w-1$位编码组成，$d_j^w$表示路径$p_w$中第j个结点对应的编码(根结点不对应编码)。
5. $${\theta }_1^w,{\theta }_2^w,...,{\theta }_{l^w-1}^w\in {\mathbb{R}}^m：路径p^w中非叶子结点对应的向量，{\theta }_j^w表示路径p^w中第j个非叶子结点对应的向量。$$

2.2.2 举例说明

既然引入了一堆符号，那么现在通过一个简单的例子来说明下
图1中由4个橙色边连起来的5个结点构成路径$p^w$，其长度$l^w$ = 5. $p_1^w,p_2^w,p_3^w,p_4^w,p_5^w$成为路劲$p^w$上的5个结点，其中$p_1^w$对应根结点。$d_1^w,d_2^w,d_3^w,d_4^w$分别为1,0,0,1,即“足球”的huffman编码为1001，此外，${\theta }_1^w,{\theta }_2^w,{\theta }_3^w,{\theta }_4^w$分别表示路径$p^w$上4个非叶子结点对应的向量。

那么，如何计算$p(w|context(w))呢$，或者说该如何计算$p(w|x_w)$,以$w="足球"$为例，从根结点到达"足球"这个叶子结点，中间总共经历了4词分支，也可以看做进行了4次2分类，在Word2vec源码中，定义左边叶子为1，右边为0，同时定义1为负类，0为正类。
此处引用sigmoid函数来计算概率，即一个结点被分为正类的概率为
$$\sigma (x_w^T\theta )=\frac{1}{1+e^{-x_w^T\theta }}$$
分为负类的概率为
$$1-\sigma (x_w^T\theta )$$
那么从根结点到达"足球"这个叶子结点所经历的4次二分类，每次分类对应的概率记为

1. 第一次：$p(d_2^w|x_w,{\theta }_1^w)=1-\sigma (x_w^T{\theta }_1^w)$
2. 第二次：$p(d_3^w|x_w,{\theta }_2^w)=\sigma (x_w^T{\theta }_2^w)$
3. 第三次：$p(d_4^w|x_w,{\theta }_3^w)=\sigma (x_w^T{\theta }_3^w)$
4. 第四次：$p(d_5^w|x_w,{\theta }_4^w)=1-\sigma (x_w^T{\theta }_4^w)$

所以 $p(足球|content(足球))={\prod }_{j=2}^{5}p(d_j^w|x_w,{\theta }_{j-1}^w)$

2.2.3 loss and 梯度上升法

cbow实现的是：在已知w的背景词的情况下，预测中心词为w的概率最大。
即：最大化 $p(w|content(w))={\prod }_{j=2}^{l_w}p(d_j^w|x_w,{\theta }_{j-1}^w)$
其中
$$p(d_j^w|x_w,{\theta }_{j-1}^w)=\{\begin{array}{ll}\sigma (x_w^T{\theta }_{j-1}^w)& d_j^w=0\\ 1-\sigma (x_w^T{\theta }_{j-1}^w)& d_j^w=1\end{array}$$
则
$$p(d_j^w|x_w,{\theta }_{j-1}^w)={\sigma (x_w^T{\theta }_{j-1}^w)}^{1-d_j^w}\cdot [1-\sigma (x_w^T{\theta }_{j-1}^w){]}^{d_j^w}$$
将此公式运用到字典C中，即希望最大化
$$\prod _{w\in C}p(w|content(w))=\prod _{w\in C}\prod _{j=2}^{l_w}{\sigma (x_w^T{\theta }_{j-1}^w)}^{1-d_j^w}\cdot [1-\sigma (x_w^T{\theta }_{j-1}^w){]}^{d_j^w}$$
此公式取log，引入对数似然函数，使得
$$L=\sum _{w\in C}\sum _{j=2}^{l^w}(1-d_j^w)\cdot log[\sigma (x_w^T{\theta }_{j-1}^w)]+d_j^w\cdot log[1-\sigma (x_w^T{\theta }_{j-1}^w)]$$
为了求导方便，将上式中2个求和下的公式简记为:

$$L=\sum _{w\in C}\sum _{j=2}^{l^w}l(w,j)$$
即
$$l(w,j)=(1-d_j^w)\cdot log[\sigma (x_w^T{\theta }_{j-1}^w)]+d_j^w\cdot log[1-\sigma (x_w^T{\theta }_{j-1}^w)]$$
至此，已经推导出对数似然函数L为cbow模型的目标函数，word2vec中采用随机梯度上升法来求解目标函数
随机梯度上升法：每取一个样本(context(w),w),就对目标函数中的所有相关参数做一次更新，每次循环更新的参数包括
$$x_w,{\theta }_{j-1}^w,w\in C，j=2,3,...,l_w$$
为此，先给出$l(w,j)$关于这些向量的梯度
$l(w,j)关于{\theta }_{j-1}^w的梯度计算：$
$$\begin{array}{rl}\frac{\partial l(w,j)}{\partial {\theta }_{j-1}^w}& =\frac{\partial }{\partial {\theta }_{j-1}^w}\{(1-d_j^w)\cdot log[\sigma (x_w^T{\theta }_{j-1}^w)]+d_j^w\cdot log[1-\sigma (x_w^T{\theta }_{j-1}^w)]\}\\ & =(1-d_j^w)[1-\sigma (x_w^T{\theta }_{j-1}^w)]x_w-d_j^w\sigma (x_w^T{\theta }_{j-1}^w)x_w\\ & =\{(1-d_j^w)[1-\sigma (x_w^T{\theta }_{j-1}^w)]-d_j^w\sigma (x_w^T{\theta }_{j-1}^w)\}{x}_w\\ & =[1-d_j^w-\sigma (x_w^T{\theta }_{j-1}^w)]x_w\end{array}$$
于是，${\theta }_{j-1}^w$的更新公式为
$${\theta }_{j-1}^w:={\theta }_{j-1}^w+\eta [1-d_j^w-\sigma (x_w^T{\theta }_{j-1}^w)]x_w$$
其中$\eta$表示学习率，下同。
可得
$$\frac{\partial l(w,j)}{\partial x_w}=[1-d_j^w-\sigma (x_w^T{\theta }_{j-1}^w)]{\theta }_{j-1}^w$$
我们的最终目的是要求词典D中每个词的词向量，而这里的$x_w$表示的是context(w)中各词词向量的均值，那么如何利用$\frac{\partial l(w,j)}{\partial x_w}$来对$v(w),w\in context(w)$进行更新？
word2vec的做法很简单，直接取
$$v(w):=v(w)+\eta \sum _{j=2}^{l^w}\frac{\partial l(w,j)}{\partial x_w},w\in context(w)$$
即把${\sum }_{j=2}^{l^w}\frac{\partial l(w,j)}{\partial x_w}$贡献到context(w)的每一个词的词向量上。因为$x_w$本身就是有context(w)中每个词的词向量的均值，求完梯度也应该讲此梯度贡献到每个分量上去。

2.2.4 cbow参数更新伪代码

1. e=0
2. $x_w={\sum }_{u\in context(w)}v(u)$
3. For $j=2:l^w$
   {
   3.1 $q=\sigma (x_w^T{\theta }_{j-1}^w)$
   3.2 $g=\eta (1-d_d^w-q)$
   3.3 $e:=e+g{\theta }_{j-1}^w$
   3.4 ${\theta }_{j-1}^w:={\theta }_{j-1}^w+g{x}_w$
   }
4. For $u\in context(w)$
   {
   $v(u):=v(u)+e$
   }
   注释：结合伪代码，给出与word2vec源码中的对应关系如下:syn0对应$v(\cdot )$,syn1对应${\theta }_{j-1}^w$,neu1对应$x_w$,neu1e对应e

3. skip-gram模型

skip-gram模型的网络结构同cbow的差不多，都是分为3层：输入层、投影层和输出层。但是与cbow不同，cbow的将背景词的词向量求平均在投影层生成$x_w$向量，输出也是一颗huffman树。

3.1 原理图

skip-gram：在已知中心词$v_w$的情况下，预测背景词context(w)。
首先先看3个层：

1. 输入层： 只包含当前样本中心词w的词向量$v_w\in {\mathbb{R}}^m$
2. 投影层：当前样本中心词w的词向量$v_w\in {\mathbb{R}}^m$，这是个恒等投影，只是为了和cbow的网络结构作对比。
3. 输出层： huffman树

3.2 梯度计算

对于skip-gram来说，已知当前词w，需要对其上下文context(w)中的词做预测。因此目标函数应该是中心词w对每个背景词的条件概率，skip-gram模型将其定义为
$$p(context(w)|w)=\prod _{u\in context(w)}p(u|w)$$
然而，如果使用此目标函数，每次迭代都只能更新$v(w)$这一个输入的向量,并不能对背景词中词向量进行更新。
所以skip-gram在Word2vec源码中做出了修改
我们在希望最大化
$$\prod _{u\in context(w)}p(u|w))$$
的同时，我们也希望
$$\prod _{u\in context(w)}p(w|u)$$
可以得到最大化，这与cbow的思想一摸一样，只是从更新背景词中2c个词向量的均值$x_w$变为直接更新背景词中的2c个输出的词向量，也就是损失函数直接对$u(i),i=1,2,3,4,...2c$进行求导。
也可变相理解为:cbow的输入是2c个背景词的均值向量，而skip-gram的输入直接是2c个背景词词向量，这样可以直接对2c个背景词的词向量单独计算梯度进行向量更新，效果远好于单独对一个字w的词向量进行更新。

3.2.1 伪代码

{
for i =1 to 2c：
$e=0$
\qquad for   j = 2   to   $l^w$：
$q=\sigma (u_i^T{\theta }_{j-1}^w)$
$g=\eta (1-d_j^w-q)$
$e:=e+g{\theta }_{j-1}^w$
${\theta }_{j-1}^w:={\theta }_{j-1}^w+g{u}_i$
$u_i:=u_i+e$
}