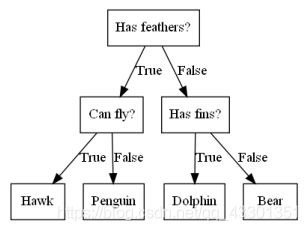
【6】决策树

决策树广泛用于分类和回归问题。比如我们要区分四种动物：鹰、企鹅、海豚、熊，我可以由几个if/else来判断，

import numpy as np
import pandas as pd
import mglearn
import matplotlib.pyplot as plt
import graphviz
from sklearn.model_selection import train_test_split

mglearn.plots.plot_animal_tree()

注意，如果报错 python导入graphviz报错：failed to execute [‘dot’, ‘-Tpdf’, ‘-O’, ‘network.gv’], make sure the Graphviz… ，解决方法如下：
（1）首先pip，
pip install -i https://pypi.doubanio.com/simple/ graphviz
（2）然后去graphviz官网下载对应自己电脑系统的graphviz程序，将graphviz程序安装在电脑上，
（3）先添加用户变量PATH，注意不要删除PATH原有的内容，在原有内容后边加一个英文状态的;，然后将安装后的graphviz程序对应的路径粘贴在;后，点击确定。
（4）然后添加系统变量，因为我的系统变量里没有PATH，所以我新建了PATH，同样的，将安装后的graphviz程序对应的路径粘贴进去，点确定。
（5）然后关掉jupyter notebook，重新打开一次，就可以了。

如果树中某个结点所包含的数据点的目标值都相同，那么这个叶结点就是“纯的”。如果要对新数据点预测，首先判定这个点位于特征空间划分的哪个区域，然后将该区域的多数目标值（如果是纯的叶结点，就是单一目标值）作为预测结果。同样，决策树也可以用于回归任务，方法相同，基于每个结点的测试进行遍历，最终找到新数据点所属的叶结点，这一数据点的输出即为此叶结点中所有训练点的平均目标值。

如果所有叶结点都是纯的叶结点，这样的模型会非常复杂，模型高度过拟合。防止过拟合有两种策略：一种是及早停止树的生长，叫“预剪枝”;另一种是先构造树，然后删除或折叠信息量很少的结点，叫“后剪枝”。

在乳腺癌数据集上详细看一下预剪枝的效果，默认将树完全展开，

from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier
cancer=load_breast_cancer()
X_train,X_test,y_train,y_test=train_test_split(
    cancer.data,cancer.target,stratify=cancer.target,random_state=42)
tree=DecisionTreeClassifier(random_state=0)
tree.fit(X_train,y_train)
print('训练集准确度：{:.3f}'.format(tree.score(X_train,y_train)))
print('测试集准确度：{:.3f}'.format(tree.score(X_test,y_test)))

训练集准确度：1.000
测试集准确度：0.937

不出所料，训练集的精度为100%，这是因为叶结点都是纯的。所以我们要在过拟合之前阻止树的完全展开，一种选择是在达到一定的深度之后停止树的展开，这里我们设置max_depth=4，这意味着这可以连续问4个问题，

tree=DecisionTreeClassifier(max_depth=4,random_state=0)
tree.fit(X_train,y_train)
print('训练集准确度：{:.3f}'.format(tree.score(X_train,y_train)))
print('测试集准确度：{:.3f}'.format(tree.score(X_test,y_test)))

训练集准确度：0.988
测试集准确度：0.951

我们可以使用tree模块的export_graphviz函数来将树可视化，这个函数会生成一个.dot格式的文件，

from sklearn.tree import export_graphviz
export_graphviz(tree,out_file="tree.dot",class_names=["malignant","benign"],
               feature_names=cancer.feature_names,impurity=False,filled=True)

读取这个.dot文件，使其可视化，

import graphviz
with open("tree.dot") as f:
    dot_graph=f.read()
graphviz.Source(dot_graph)

此处结果图无法展示

树的可视化有助于解释，不过，这里树的深度只有4层，也有点大了；一种可用的观察树的方法是，找出大部分数据的实际路径。除此之外，我们还可以利用一些有用的属性来总结树的工作原理，其中最常用的是“特征重要性”，它为每个特征对树的决策的重要性进行排序，对于每个特征来说，它都是一个介于0和1之间的数字，其中0表示根本没用到，1表示完美预测目标值。特征重要性的求和始终为1.

print("特征重要性：\n{}".format(tree.feature_importances_))

特征重要性：
[0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.01019737 0.04839825
 0.         0.         0.0024156  0.         0.         0.
 0.         0.         0.72682851 0.0458159  0.         0.
 0.0141577  0.         0.018188   0.1221132  0.01188548 0.        ]

我们可以将特征重要性可视化，

def plot_feature_importances_cancer(model):
    n_features=cancer.data.shape[1]
    plt.barh(range(n_features),model.feature_importances_,align='center')
    plt.yticks(np.arange(n_features),cancer.feature_names)
    plt.xlabel("Feature importance")
    plt.ylabel("Feature")
plot_feature_importances_cancer(tree)

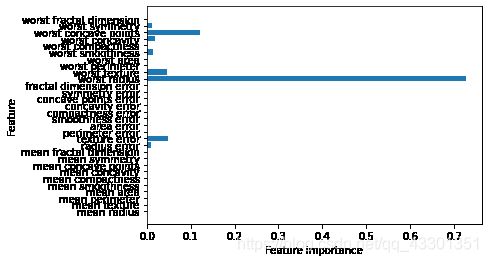
如果某个特征很小，并不能说明这个特征没有提供任何信息，只能说明该特征没有被树选中，可能是因为另一个特征也包含同样的信息。
与线性模型的系数不同，特征的重要性始终为正数，也不能说明该特征对应哪个类别。它只是告诉我们某个特征很重要，但并未告诉我们该特征大对应的是哪一类。在特征和类别之间可能没有简单的关系。

tree=mglearn.plots.plot_tree_not_monotone()
display(tree)

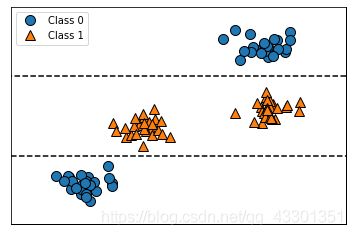
我们可以看出，特征和类别之间并不是单调关系。
回归树和分类树类似，但需要注意的是，所有的基于树的回归模型，都不能外推。

ram_prices=pd.read_csv("ram_price.csv")
plt.semilogy(ram_prices.date,ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")

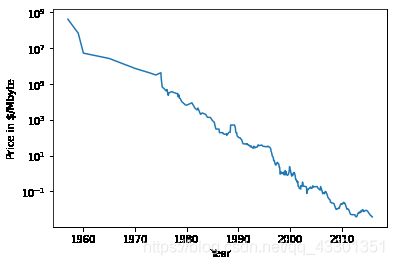
在用对数坐标绘图时，二者的线性关系看起来非常好。
我们利用2000年前的历史数据来预测2000年后的价格，只使用日期作为特征，对两个简单的模型进行对比：DecisionTreeRegressor和LinearRegression。对价格取对数，使得两者的线性关系相对较好。这对DecisionTreeRegressor影响不大，却对LinearRegression影响很大。训练模型并作出预测之后，我们来做对数逆运算来使数据恢复原貌。

from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
#利用历史数据来预测2000年后的价格
data_train=ram_prices[ram_prices.date<2000]
data_test=ram_prices[ram_prices.date>=2000]

#基于日期来预测价格
X_train=np.array(data_train.date).reshape(-1,1)#变为1列


#我们利用对数变换得到数据和目标之间更简单的关系
y_train=np.log(data_train.price)
tree=DecisionTreeRegressor().fit(X_train,y_train)
linear_reg=LinearRegression().fit(X_train,y_train)

#对所有数据进行预测
X_all=np.array(ram_prices.date).reshape(-1,1)#变为1列
pred_tree=tree.predict(X_all)
pred_lr=linear_reg.predict(X_all)

#对数变换逆运算
price_tree=np.exp(pred_tree)
price_lr=np.exp(pred_lr)

plt.semilogy(data_train.date,data_train.price,label="Training data")
plt.semilogy(data_test.date,data_test.price,label="Test data")
plt.semilogy(ram_prices.date,price_tree,label="Tree prediction")
plt.semilogy(ram_prices.date,price_lr,label="Linear prediction")
plt.legend()

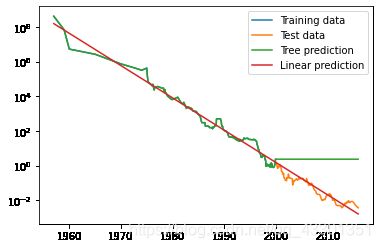
两个模型之间的差异非常明显，线性模型对数据的近似很好，预测也很好。树模型则完美预测了训练集，由于没有规定树的复杂度，因此它记住了整个数据集。但一旦预测数据范围超过了训练数据的范围，树变得无法预测，即树无法再训练集外进行预测。
决策树优点：模型容易可视化，专家容易理解；算法不受数据缩放的影响。
决策树缺点：即使做了预剪枝，也容易过拟合，泛化性能比较差。