Python 刷题笔记:贪心算法专题一
LeetCode 每月都会搞每日一题活动,昨天的题目是贪心算法类型,折腾好久才做出来,索性今天就围绕贪心算法多看几道。
首先明确下贪心算法概念:
贪心算法从问题的某个初始解出发,逐步逼近给定的目标,以便尽快求出更好的解。当达到算法中的某一步不能再继续前进时,就停止算法,给出一个近似解。
《Python 算法详解》张玲玲
贪心算法的基本思路如下:
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每一子问题求解,得到子问题的局部最优解
- 把子问题的局部最优解合并成原来问题的一个解
实现该算法的基本过程如下:
- 从问题的某一初始解出发
- while能向给定总目标前进一步
- 求出可行解的一个解元素
- 由所有解元素组合成问题的一个可行解
空洞的文字说明总是难以准确描述,我们直接看题。
题目一
第 45 题:跳跃游戏 II
难度:困难
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
#来源:力扣(LeetCode)
#链接:https://leetcode-cn.com/problems/jump-game-ii
说明: 假设你总是可以到达数组的最后一个位置。
题目分析
按照贪心算法的基本思路,题目中要求最小跳跃次数,可以转化为设计跳跃路线问题,再具体到每一步的话就是下一次跳跃的位置选择问题。只要我们每一次跳跃都是当前最好的选择,那么跳到最后次数应该会是最优解。
但注意,贪心算法是存在缺陷的:它并不能保证最后的解是最优的;也适合用来求最大解或最小解问题;只能求满足某些约束条件的可行解的范围。我们初接触贪心算法,只能通过不断的题目练习才能体会其中的道理。
思路尝试
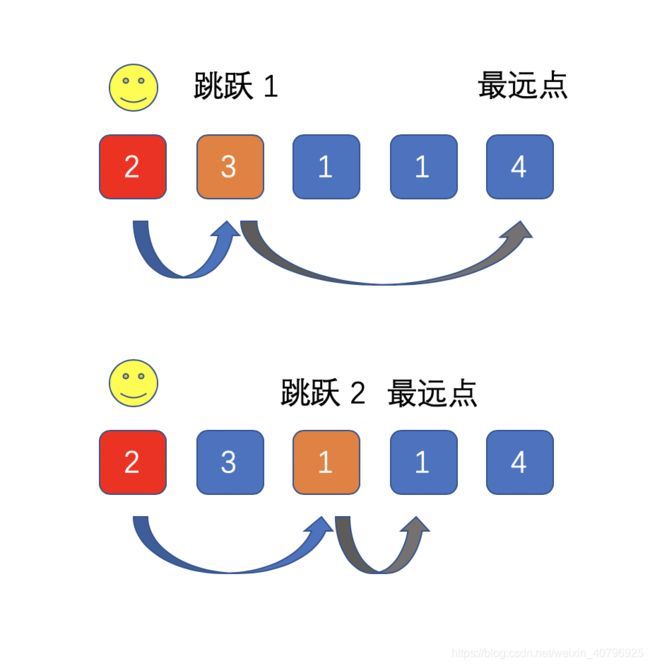
认定贪心算法做思路,我们来设计算法,直接看示例:[2,3,1,1,4],我们位于首位 2,可跳的距离范围是 1 到 2。我们的目标是最少次数到最后,所以选择跳的点所能触及距离越远越好:
如图,只要我们选择所能接触距离最远的位置来跳跃,便可能达到最优解,这个最远位置是要跳的位置坐标 j 与其值 nums[j] 的和。基于此,我们可以设计代码。当然其中还会遇到特殊情况,比如我能接触最远范围的点上值为 0,这就导致选择了这点相当于进了死胡同,后面就没法跳了,这些额外情况可能最初写代码并不会兼顾到,需要不断测试优化才能解决。
代码实现
class Solution:
def jump(self, nums: List[int]) -> int:
# 列表长度
length = len(nums)
# 只有一个元素的列表,不用跳
if length<=1:
return 0
# 首位值就能跳到最后的列表,直接返回 1
if nums[0]>=length-1:
return 1
# count 用于统计跳跃次数
count = 0
# i 即此时我们所处位置
i = 0
# 用于记录比较不同选择间所能接触的最大距离
max_step = 0
# 记录要跳跃的距离
jump = 0
# 只要我们位置没有到最后一位,就进入 while 循环
while i<length - 1:
# 位于 i 位置,可选的跳跃距离是 1 到 nums[i],for循环遍历比较
for j in range(1,nums[i]+1):
# j是我们要跳的距离,nums[i+j]即目标位置所能跳的最大距离
# step 即我们的选择所能触及的最大距离
step = j + nums[i+j]
# 如果跳完直接到达最后或超出,那么返回次数+1
if i+j>=length-1:
return count+1
# 如果跳完位置还没到最后,检查最大距离能不能到达,若能,连跳两次完成任务
elif step>=length-1:
return count+2
# 如果最大距离还没到最后,我们就需要比较不同选择间的最大距离
else:
# 注意,排除掉目标位置上值为 0 的死路情况
if nums[i+j]!=0:
# max_step 处于 for 循环中记录遍历到的较大值
max_step = max(max_step,step)
# 如果此时与最大值情况相符
if step==max_step:
# jump 记录最大情况下要跳的距离
jump=j
# for 循环结束,我们要跳 jump 距离
i+=jump
# 跳跃次数 +1
count+=1
# 要把刚记录的距离较大值清零,方便下一次循环重新计算
max_step = 0
# 返回记录的次数
return count
提交测试结果:
执行用时 : 76 ms, 在所有 Python3 提交中击败了 46.10% 的用户
内存消耗 : 15.1 MB, 在所有 Python3 提交中击败了 12.50% 的用户
别看代码中考虑的额外情况不算多,但这是接近修改了 20 此才通过的代码。如若不是题目带着贪心算法标签,可以肯定这思路能拿到答案,半道都要放弃了。
题目二
第 1282 题:用户分组
难度:中等
有 n 位用户参加活动,他们的 ID 从 0 到 n - 1,每位用户都 恰好 属于某一用户组。给你一个长度为 n 的数组 groupSizes,其中包含每位用户所处的用户组的大小,请你返回用户分组情况(存在的用户组以及每个组中用户的 ID)。
你可以任何顺序返回解决方案,ID 的顺序也不受限制。此外,题目给出的数据保证至少存在一种解决方案。
示例 1:
输入:groupSizes = [3,3,3,3,3,1,3]
输出:[[5],[0,1,2],[3,4,6]]
解释:
其他可能的解决方案有 [[2,1,6],[5],[0,4,3]] 和 [[5],[0,6,2],[4,3,1]]。
示例 2:
输入:groupSizes = [2,1,3,3,3,2]
输出:[[1],[0,5],[2,3,4]]
#来源:力扣(LeetCode)
#链接:https://leetcode-cn.com/problems/group-the-people-given-the-group-size-they-belong-to
题目分析
这题虽然挂着个贪心算法的标签,但没有能明显感受到贪心算法的应用。即使解决完题目后去翻看题解,因为是比较靠后的题目,题解不多且对贪心算法的说明也不太明显。
这题比较好理解,按示例 1 看,一共 7 个人,第 6 个是单人组,其余 6 个是两个三人组,所以输出结果中只要保证坐标为 5 的第六个人单独一组即可。
思路尝试
我们可以遍历这个 groupSizes 列表,比如第一位是 3,我们就用字典来记录 dic[3]=[],并将第一人的坐标塞入该列表,这样得到了 dic={3:[0]};
当我们遍历第二位时,又是 3,我们先检查字典中是否有键为 3 的列表,dic[3] 是存在的,且长度才为 1 还不满,那么就可以继续往里添加第二位。以此类推,当遍历到第四人时目前三个人已经组满 3 人小组了,就需要将成型的三人小组记录到最终结果,并将字典中的列表清空来重新记录。
代码实现
class Solution:
def groupThePeople(self, groupSizes: List[int]) -> List[List[int]]:
# 记录最终结果的列表
result = []
# 记录小组人数为键-小组成员列表为值的字典
dic={
}
# 遍历 groupSizes
for i,c in enumerate(groupSizes):
# 若不存在该键值,将其初始化为 dic[c]=[]
dic.setdefault(c,[])
# 如果 dic[c] 对应的成员列表长度已经达到了 c,即小组满员
if len(dic[c])>=c:
# 将满员小组记录到最终结果中
result.append(dic[c])
# 清空之前小组,将当前成员添加到新的列表中
dic[c]=[i]
# 若仍未满员
else:
# 在该小组列表中添加当前成员
dic[c].append(i)
# 上述过程已经将当前成员添加完毕
# 若此时小组成员满员,将小组记录到结果中,清空小组
if len(dic[c])>=c:
result.append(dic[c])
dic[c]=[]
# 返回结果
return result
提交测试表现:
执行用时 : 52 ms, 在所有 Python3 提交中击败了 98.10% 的用户
内存消耗 : 13.8 MB, 在所有 Python3 提交中击败了 12.50% 的用户
结论
贪心算法,目前我的理解是问题如果可以分步考虑,每次取最优。但还是没能理解倘若取不到最优解,是在此基础上继续补窟窿,还是重新用别的算法来做?
今天时间不太够,明天继续探索贪心算法~