用tensorflow实现线性回归案例

1、案例介绍
本次学习的目的是如何用tensorflow实现线性回归，最重要的是熟悉如何搭建一个神经网络框架，接下来这个例子的神经网络有三层，输入层-中间层-输出层。先上代码:

 import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()
import numpy as np
import matplotlib.pyplot as plt

x_data=np.linspace(-0.5,0.5,200)[:,np.newaxis]#200行一列
noise=np.random.normal(0,0.02,x_data.shape)#正态分布（均值，方差，输出）
y_data=np.square(x_data)+noise

x=tf.placeholder(tf.float32,[None,1])
y=tf.placeholder(tf.float32,[None,1])

#定义神经网络中间层
Weights_L1=tf.Variable(tf.random_normal([1,10]))#1行十列，1个输入，十个中间层神经元
biases_L1=tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1=tf.matmul(x,Weights_L1)+biases_L1
L1=tf.nn.tanh(Wx_plus_b_L1) #激活函数，中间层输出L1
#定义输出层
Weights_L2=tf.Variable(tf.random_normal([10,1]))#从服从正态分布的序列随机取出指定个数的值
biases_L2=tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2=tf.matmul(L1,Weights_L2)+biases_L2
prediction=tf.nn.tanh(Wx_plus_b_L2)

loss=tf.reduce_mean(tf.square(y-prediction))

train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
#定义会话
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(2000):
        sess.run(train_step,feed_dict={
     x:x_data,y:y_data})
    #获得预测值    
    prediction_value=sess.run(prediction,feed_dict={
     x:x_data})
        
    plt.figure()
    plt.scatter(x_data,y_data)#样本点
    plt.plot(x_data,prediction_value,'r-',lw=5)
    plt.show()

2、结果如下：

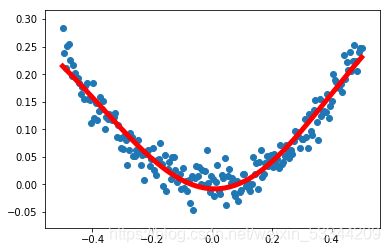
图中蓝色的散点是生成的200个样本点，红色是训练出来的拟合这些点的最佳曲线，可以看出误差很小。
其实从这里我们可以发现其中的神奇，上篇博客中我们是用线性模型拟合直接那些点，然而这里是一个类似于y=x*x的曲线，且有噪声，这是用线性模型无法拟合的，然而神经网络有这个能力，虽然其中内部的模型也是类似于y=kx+b(矩阵形式)加上激活函数,这就很神奇，神经网络可以用线性模型来拟合非线性模型，其中的道理我不详细解释了，大家可以上网搜搜。

3、具体分析
我们需要先知道两个相似的函数，np.random.normal(0,0.02,x_data.shape)，其中0代表均值，0.02代表方差，最后一个参数是输出形式，这个函数生成了200个符合该正态分布的噪音点。
tf.random_normal([1,10]),从服从正态分布的序列随机取出指定个数的值.
需要注意的是其中【1,10】代表了张量的形状[1,10]代表一个1行10列的矩阵，其实生成的是[[w1,w2,w3…w10]]。
第一层神经网络其实就是[[x]]*[[w1,w2,w3…w10]]+[[b1,b2…b10]]=
[[w1x+b1,w2x+b2,…w10x+b10]],然后加上一个激活函数，就是第一层的输出L1,第二层也是这样的推导，最后输出一个预测值，就是y的预测值。
神经网络里面的过程大致就是这样，我们通过2000次的训练，把样本丢进去，最小化误差，而最小化误差就要改变神经网络里面的一开始随机设置的权重和偏置w,b，他们都是变量。w,b都是朝着最小化误差loss的方向改变的,最终得到一个最佳的w,b。(w,b都是矩阵形式）。

到这里，我们就把这个案例背后神经网络基本的逻辑过程理清楚了，其中用到了随机梯度下降最小化误差，只需要调用就行，方便我们使用，背后的原理不难，但是要我们自己写代码的话就不简单了。
学习神经网络最好有点线性代数的基础，特别是矩阵运算，比如“左列=右行”等基本规则的熟悉。