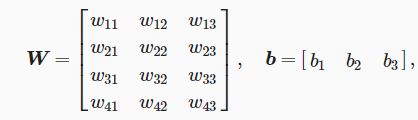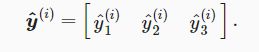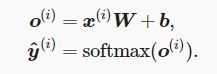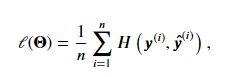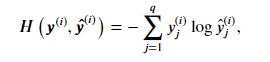深度学习-softmax回归原理和实现

softmax回归

输出单元为多个，单层神经网络，输出层为全连接层

神经网络图

运算

矢量计算表达式

softmax回归的权重和偏差参数分别为

样本特征features

输出层输出

概率分布为

矢量计算表达式为

小批量样本分类的矢量计算表达式

交叉熵损失函数

交叉熵

衡量两个概率分布的差异

图像分类数据集 Fashion-MNIST

from mxnet.gluon import data as gdata
import sys
import time

mnist_train=gdata.vision.FashionMNIST(train=True)  #训练数据
mnist_test=gdata.vision.FashionMNIST(train=False)  #测试数据

print('minist_train:',len(mnist_train))
print('minist_test:',len(mnist_test))

feature,label=mnist_train[0] #图像，标签

print('feature.shape:',feature.shape) # 大小
print('feature.dtype:',feature.dtype) # 数据类型

print('label:',label,type(label),label.dtype)

print('label的文本标签：',d2l.get_fashion_mnist_labels([2])) # 输入数组，返回文本标签

X,y = mnist_train[0:9]
d2l.show_fashion_mnist(X,d2l.get_fashion_mnist_labels(y)) # 画出标签和图像内容

softmax回归从零开始实现

import d2lzh as d2l
from mxnet import autograd,nd

# 使用Fashion-MNIST数据集
batch_size=256 # 批量大小
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)

num_inputs=784 # 样本高和宽均为28像素，输入向量长度28*28=784
num_outputs=10 # 图像有10个类别，单层神经网络输出层的输出个数为10
W=nd.random.normal(scale=0.01,shape=(num_inputs,num_outputs)) # 权重矩阵
b=nd.zeros(num_outputs) # 偏差参数矩阵

# 为参数模型附上梯度
W.attach_grad()
b.attach_grad()

# softmax运算
def softmax(X):  # X行数为样本数，列为输出个数
    X_exp=X.exp()
    partition=X_exp.sum(axis=1,keepdims=True)  # 按行求和
    return X_exp/partition

# softmax回归模型
def net(X):
    return softmax(nd.dot(X.reshape(-1,num_inputs),W)+b) # -1 为未指定行数

# 损失函数
def cross_entropy(y_hat,y):
    return -nd.pick(y_hat,y).log()

# 准确率函数
def accuracy(y_hat,y):
    return (y_hat.argmax(axis=1)==y.astype('float32')).mean().asscalar() # .asscalar将向量转换为标量

# 训练模型
num_epochs, lr = 5, 0.1 # 迭代周期数，学习率

# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter: # 样本和标签
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum() # l是有关小批量的损失
            l.backward() # 小批量的损失对模型参数求梯度
            if trainer is None:
                d2l.sgd(params, lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
            else:
                trainer.step(batch_size)  # “softmax回归的简洁实现”一节将用到
            y = y.astype('float32')
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n += y.size
        test_acc = d2l.evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,[W, b], lr)

for X, y in test_iter:
    break

true_labels = d2l.get_fashion_mnist_labels(y.asnumpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1).asnumpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]

d2l.show_fashion_mnist(X[0:9], titles[0:9])
d2l.plt.show()

softmax回归简洁实现

import d2lzh as d2l
from mxnet import gluon, init
from mxnet.gluon import loss as gloss, nn

batch_size=256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

net = nn.Sequential()
net.add(nn.Dense(10)) # 添加一个输出个数为10的全连接层
net.initialize(init.Normal(sigma=0.01)) # 使用均值为0、标准差为0.01的正态分布随机初始化模型的权重参数

loss = gloss.SoftmaxCrossEntropyLoss()

# 学习率为0.1的小批量随机梯度下降作为优化算法
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': 0.1})

num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
              None, trainer)