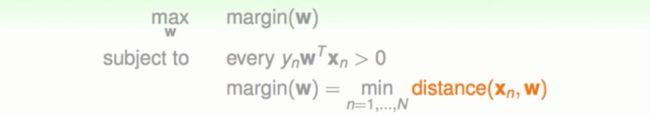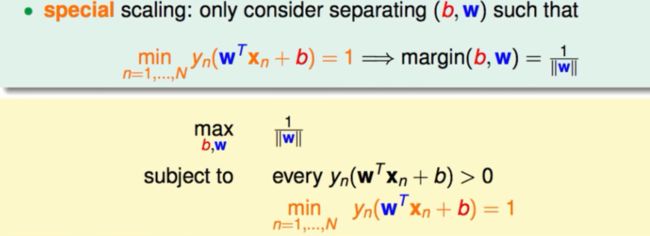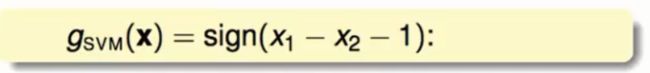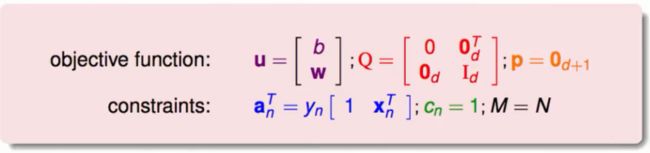机器学习之线性支持向量机(机器学习技法)
胖的就是好的(以二元分类为例)
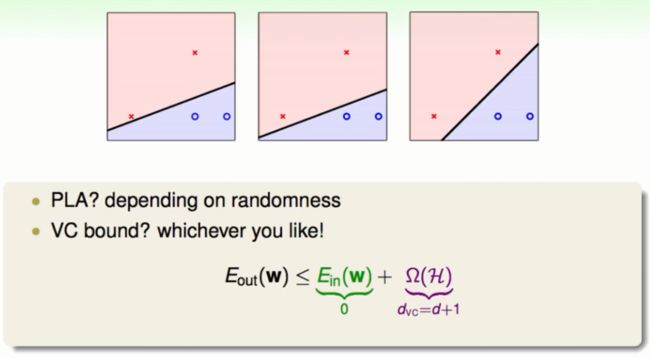
直觉的选择现在我们已经能够分割线性的资料了,但是由于以前的算法(PLA,Pocket,etc.)具有一些随机性所以我们得到的线性模型不尽相同。如下图:
在图中所有的模型(超平面)都能够分割样本中的资料,而且在VC上限的保证下这3个模型好像没有什么不同。但是仅仅凭借直觉我们可能会选择第3个仿佛有什么好处。
一个全新的角度
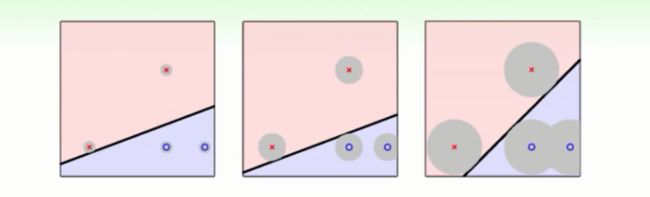
我们做机器学习的目标就是模型要在测试的资料上表现的好(Eout≈0),但是由于杂讯的随机性,测试的资料往往与训练的资料不尽相同它们可能会在训练的资料附近波动。如下图的灰色区域:
我们想要模型在判断灰色区域内的训练资料上不犯错误(在区域内的波动仅仅是代表一种资料),那么我们就要使得这个灰色区域的面积越大越好。面积越大就能够容忍更多的noise,反过来说就是模型有更好的容错性更加强固。
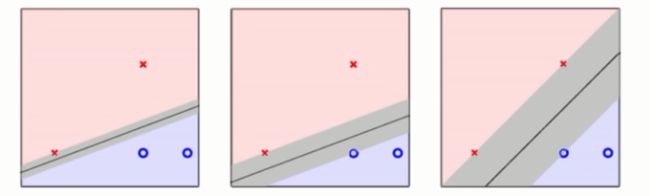
如上图,一个更加强固的模型具体体现在资料点到超平面隔很远,形象的来说是它有一个很胖的边界。具体来说就是即使离超平面最近的点也会有很长的距离。在一些文献上这个很胖的边界就叫外边距(margin)。
明确目标
所以我们现在要求这样的一个超平面它满足以下两点:
①必须能够完全正确的分割这笔资料。
②要求这个超平面的外边距最大。
同时外边距的计算方式就是计算所有资料点到超平面的距离的最小值。
总体的边界选择策略就是计算最小值选取最大值。如下图:
将问题细节化_距离的求解
距离的求解_向量分割
在距离的求解中0维的向量有着与其它向量不同的地位,为了方便计算我们将0维的向量分割出来。具体过程与改进后的假设模型如下图:
图中从0维分割出来的b的几何意义就是得分函数的截距。
距离的求解_超平面的法向量
中学时我们知道,平面外一点到平面的距离等于这一点到平面内任意一点连线的距离在该平面法向量上的投影的长度。所以我们先求解法向量。
如上图所示我们随便找到平面上的两点x`与x``,将这两点带入超平面的表达式得到①的两个式子,在将①中的两个式子相减得到②同时也得到了W就是平面的法向量。
距离的求解_终章
最后点x到超平面的距离如下:
将问题细节化_条件的转换
去掉绝对值
由于超平面严格的二分,我们资料的标签与我们的预测是相同的,则上图可以进一步表述为下图:
总结一下我们的问题如下图所示:
同比放缩
在数学上很多的等式在同比放缩之后会有相同的实质,所以我们把上面的式子进行同比放缩。我们令y*h(x) = 1这样的话每个点到超平面的距离就等于1/||W||。同时我们要解决的问题也发生了转换如下图:
这个新问题的条件想对于以前更加苛刻(以前是y*h(x)>0现在是y*h(x)=1)。
更为宽松的条件
在上图中我们的最终求解需要经过min y*h(x) = 1的过程和max 1/||W||的过程使得问题比较复杂。下面我们做的就是将最小化这个条件转化为一个非最小化的条件。新条件是y*h(x) >=1。以下是为什么min y*h(x) = 1可以转化成y*h(x) >=1的推导。
如果y*h(x) >1假设为n,则我们要求的最优解要想维持以前的值不变也需要同比的放缩,也就是现在的||W|| = ||W||/n那么在这种条件下我们现在的1/||W||会比起原来的最优解还大,矛盾了!所以结论是我们看起来去掉了最小化的过程但事实上在新条件y*h(x) >=1下我们最优化的结果与min y*h(x) = 1的条件下是一样的。然后我们将问题稍作变化得到一个新的问题,整个如下图:
转换后的问题我们一般称之为标准问题。
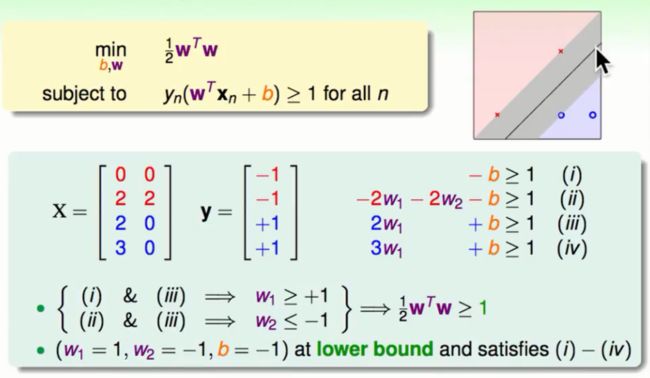
解决一个特别的问题
将空间中不同的四个点的坐标与对应的标签带入标准问题中,经过简单的化简会得到(1/2)W²>=1。再将一组特殊的解W1 = 1,W2 = -1,b = -1带入标准问题中会得到W²的最小值同时也得到了以下的学习模型:
这正是图中的那一条一次曲线,从直觉上来看这是一条比较胖的线。这个学习模型就是我们所推倒的SVM。
为什么叫做支撑向量机
在上述的例子中离超平面最近的点(是一个向量)唯一决定了这个超平面,而其它的点的存在对这个平面位置的决定没有任何的帮助。我们就可以想象这些离超平面最近的点支撑起了这个超平面,这些点就叫做支撑向量它们所支撑的这个模型叫做支撑向量机(support vector machine)。
解决一个普通的SVM问题
二次规划的引出
我们再次审视刚才的标准问题它有这些特征:
①它所最优化的问题是一个二次式
②它的限制条件是一个线性的一次式
有这样特性的最佳化问题就叫二次规划(quadratic programing 以下简称QP)。
QP问题通常会使用其它软件去轻松解决。
将标准问题转换成QP问题
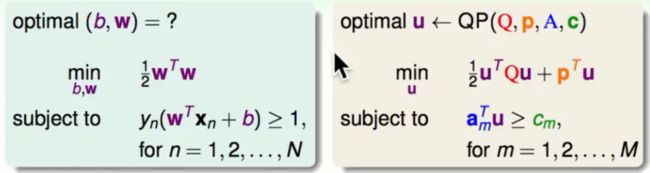
首先对照我们的标准问题与QP问题
左面是标准问题,右面是QP问题。以下为QP问题的参数详解:
u:我们要求得最优二次式(包括一次项与二次项)
Q:二次项系数
p:一次项系数
a:条件中u向量的一次式的系数
A:小a的集合
c:大于某一个常数的那个常数
C:小c的集合
M:有多少个一次式的条件
①我们最优化的二次式中包含W与b,所以u的向量中包含b与W
②有关二次项系数由于式子中只是(1/2)W²所以在Q矩阵中有关于b的部分都为0,有关于W的为单位矩阵。
③一次项系数为0,所以p为0向量
④在条件的一次式中经过移项之后会得到y[1 x]就是a的值
⑤c很简单就是1
⑥M很简单就是N
所有的转换就绪如下图:
实务上我们在使用QP的软件的时候要仔细读一下说明书有的转化略有不同,需要稍微的改动。
在得到上述的参数之后,我们做的就是将上述的参数丢到一个软件里最后得到一个支撑向量机,如下图:
小结
得到的模型我们称之为Linear hard-margin SVM
hard-margin:我们坚持将资料完全分开。
linear:我们的资料没有经过非线性的特征转换。
最后如果想要得到一个非线性的模型就可以像以前一样经过一些特征转换将原来的线性空间的资料转换到一个非线性空间去就可以解决。
SVM的好处与理论上的保障
SVM与正则化
SVM中的宽的边界与我们以前学过的正则化有很多相似的地方:
在正则化中我们的目标就是最小化Ein约束条件就是W²<=C,在SVM中我们目标就是最小化W²同时限制条件是Ein = 0。但是总结起来就是无论是正则化还是SVM的宽的边距都是同时在做好最小化Ein与W²,只是位置发生了交换。所以从某种程度上来说SVM的LargeMargin就是一种正则化。
SVM理论上的保障
在讨论VC维度的时候我们判定一个假设模型的复杂度的直观体现就是这个模型能够完全分割资料点的个数。能够分割的资料点越多说明这个模型的复杂度就越高,越有力量。
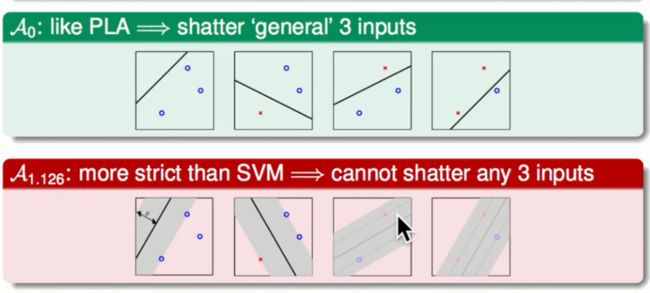
在SVM中我们的演算法想要找出胖胖的边界,我们会选择胖过某一个门槛值的模型,这样的话会使得我们的有效的模型的个数会减少。如下图:
上图是一些二元分类的模型,在不计较胖瘦边界的时候我们会得到所有的分割情况。在计较胖瘦的情况下我们就不能分割这些资料点的所有情况。在VC维度中的观点就是不能分割所有点的模型它的模型复杂度较低,有效的VC维度就月底会使得Eout与Ein越接近。
演算法的VC维度
事实上演算法的VC维度是没有严格的定义的。演算法的VC维度比普通的VC维度需要更多的条件:它会与我们拿到的资料有关。
比如在一个单位圆中如果不考虑胖瘦(ρ = 0)则演算法的复杂度为3,如果我们限制ρ>二分之根号三的话则演算法的复杂度会小于3。但所有的资料中必须有一些资料的距离小于根号三。
最后我们得到:我们可以通过调节模型边界的胖瘦来控制演算法的VC维度。
LargeMargin的好处
在以前不考虑胖瘦的情况下在VC维度很小的情况下它的复杂度较小Ein≈Eout但是它不能分割复杂的资料,当它的复杂度高的时候我们能够分割复杂的资料但是Ein会与Eout隔很远始终不能两全我们只能做一个适当的权衡。LargeMargin的复杂度会更加小一些Ein≈Eout但是它不能分割复杂的资料。但是我们把LargeMargin与特征转换结合起来的话我们既可以得到不太高的VC维度同时又能分割出一个复杂的边界:
从此我们又有了一个新的控制复杂度的方式。