使用全局形状正则化在3-D OCT图像中概率的视网膜内层分割
Probabilistic intra-retinal layer segmentation in 3-D OCT images using global shape regularization
使用全局形状正则化在3-D OCT图像中概率的视网膜内层分割
摘要
随着光谱域光学相干断层扫描(OCT)的引入,导致采集速度的显着提高,3-D OCT扫描的快速和准确分割变得越来越重要。本文提出了一种新的概率方法,模拟视网膜层的外观以及层边界的整体形状变化。给定OCT扫描,使用变分方法近似推断分割上的完全后验分布,从而能够在计算上易处理的模型组件方面实现有效的概率推断:分割完整的3-D体积需要大约一分钟。准确的分割证明了使用全局形状正则化的好处:我们分割了35个中心凹3-D体积,平均无符号误差为2:46 0:22 lm以及80个正常和66个青光眼2-D循环扫描,误差为分别是2:92 0:5 lm和4:09 0:98 lm。此外,我们利用推断的后验分布来评估分割的质量,指出潜在的错误区域并区别于病理扫描。不需要预处理或后处理,我们对所有数据集使用相同的参数集,强调了我们方法的稳健性和开箱即用性
1介绍
光学相干断层扫描(OCT)是一种体内成像技术,用于测量反向散射光的延迟和幅度。提供微米分辨率和毫米穿透深度到视网膜组织(Drexler和Fujimoto,2008),OCT非常适合眼科成像。由于没有其他方法可以用这样的分辨率进行非侵入性成像,OCT已成为临床眼科学的标准(Schuman等,2004)。一些研究表明适用于诊断青光眼或年龄相关性黄斑变性等疾病(Bowd等,2001; Zysk等,2007)。光谱域OCT的最近引入(de Boer等人,2003; Wojtkowski等人,2002)显着提高了成像速度并且能够获得包含数百个B扫描的3-D体积。由于视网膜层的手动分割是繁琐且耗时的,因此随着收集的数据量的增加,自动分割变得越来越重要。此外,除了分割结果之外,能够推断估计的不确定性的概率模型为从业者提供必要的信息。
已发表的有许多方法用于OCT图像中的视网膜分割任务。所有这些都有共同点,它们基于强度或梯度信息生成外观术语。 最重要的是应用正则化,这使得预测对于由血管引起的散斑噪声或阴影更加稳健。 为了对这一广泛的方法提供系统的概述,我们选择通过用于正规化的方法来区分它们。
一个主要类别是基于规则的启发式技术(Ahlers等人,2008;Fernández等人,2005; Ishikawa等人,2005; Mayer等人,2010),其例如应用异常值检测和线性 插值以解释错误的分段。 其他方法(Baroni等,2007; Yang等,2010)对每个边界的单个马尔可夫链使用动态规划,并约束相邻边界位置之间的最大垂直距离。 Vermeer等人。 (2011)使用支持向量机对像素进行分类,并使用水平集技术对输出进行调整。 这些方法都没有包含形状先验信息。
主动轮廓方法包括梯度和基于强度的方法(Mishra等,2009; Yazdanpanah等,2009,2011)。 Yazdanpanah等。 (2009,2011)通过简单的圆形形状在先增加经典主动轮廓功能。 所有三种方法仅在排除中心凹区域的OCT扫描上进行测试,因此主要包含具有相当简单形状的平坦边界。
一系列更先进的方法(Antony等人,2010; Dufour等人,2013; Garvin等人,2009; Song等人,2013)构建了一个几何图形,以同时分割三维OCT中的所有边界 体积。 与先前提出的方法不同,它们考虑了相邻边界的相互作用以相互限制它们的相对位置。 该形状先验信息作为硬约束被编码到图中(Antony等人,2010; Garvin等人,2009),或者如Song等人最近引入的那样。 (2013年),随后由Dufour等人延长。 (2013),作为概率软约束。 然而,由于计算限制,仅包括局部形状信息并且分阶段地划分边界。
最后,Kajic’等人。(2010)将与外观和形状的统计模型匹配的流行的主动外观模型应用于给定的OCT扫描。 尽管非局部形状建模在其方法的范围内,但它们仅使用地标,即稀疏采样的边界位置而不是完整的形状模型。 此外,仅推断出最大似然点估计,而不是形状上的分布。
1.1贡献
我们提出了一种新的OCT视网膜分割问题的概率方法。 我们的概率图形模型将外观模型与全局形状先验相结合,包括边界之间的局部和长程(long-range)相互作用。 模型的离散部分具有高度可并行化的柱状离散分割,但仍然考虑了所有其他图像列。 为了推断该模型的后验概率,我们利用变分推理,一种确定性近似框架。
据我们所知,这是唯一的工作,其中完整的全局形状先验被用于OCT视网膜分割的任务。 此外,我们还没有意识到任何其他分段方法可以推断出完整的概率分布。 我们的方法提供了出色的分割性能,优于依赖于局部或无形状正规化的方法,以及病理检测和分割质量评估。 图1显示了分段边界,但如果可以获得地面实况,则可以轻松地将外部限制膜(ELM)等附加边界纳入其中。
这项工作是根据先前的一份会议论文(Rathke等,2011)提出的初步想法发展而来的。
1.2组织
下一节将介绍我们的概率图形模型。 第3节通过变分推理评估后验分布,并且我们在有效可解凸凸问题方面解决了第4节中的相应优化问题。 第5和第6节介绍了我们用于评估的数据集和相应的结果。 我们在第7节中总结了未来工作的讨论和可能的方向。
2.图形模型
本节介绍了我们的概率图模型,分别对OCT扫描y及其分割b和c进行统计建模。 我们引入c,连续边界向量b的离散化版本,以在数学上明确y的离散像素域与b的连续边界域之间的连接。
我们的假定(ansatz)是由
![]() 因子
因子
| p(y丨c) | 外观,数据似然项, |
| p(c丨b) | 马尔可夫随机场正则化器,由形状先验和全局形状先验确定。 |
| p(b) | 全局形状先验 |
在下文中,我们将详细说明每个组件,从而完成我们的图形模型的定义。 图2根据各个模型层的连通性说明了我们的图形模型。
2.1。 符号
整篇论文使用以下符号:
| N,M | OCT扫描尺寸(行,列) |
| Nb | 分割边界的数量; 本文中Nb = 9; |
| i,j,k | 相应指数:i = 1, … ,N; j = 1, … ,M; k = 1, … , Nb |
| bk,j∈R | j列中边界k的实值位置; |
| ck,j ∈{1,…,N} | 整数值边界变量,类似于b,但指定像素网格上的行位置; |
| xi,j ∈ X | 表示图层或过渡类成员资格的类变量; |
| yi,j | 观察数据; 这里的像素(i,j)周围的斑块(patch)投射到低维流形上 |
| ∆N |
符号●表示相应索引的所有元素的集合,例如bk,● ∈ RM 是边界k的位置矢量。 通过b\j,我们表示集合b\b●,j,用类似的符号表示μ和∑。有关这里介绍的大多数符号的说明,请参见图3。
2.2外观模型
我们利用高斯分布来模拟视网膜层的外观以及边界。给定分段假设c,我们可以为每个像素分配类别标签xi; j∈ X,它们的范围由下式给出
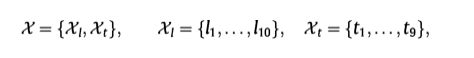
p的时刻由Eb和Vb给出。 同样,R也可以分解为W和r2I。 利用这些分解,可以降低与R或R1相关的大多数操作的复杂性以及存储器要求,因为只需要存储W和r2。 p的参数可以通过最大对数似然估计。 W由具有最大特征值的(加权的)qppca特征向量组成,从经验协方差矩阵计算。 有关详细信息,请参阅Tipping和Bishop(1999)。
对于符合(2)的c的所有配置,右边的概率分别使用条件边际密度p和pp计算。边际pbk提供了一种将全局形状知识引入我们的列式图形模型的方法pcjb。
其中qc是离散概率分布。 类似地,通过qk,我们表示变量对ckj上的离散概率分布。 要使qc成为有效分布,必须满足额外的边际化约束:
2.3形状先验
作为由于生物变异性和图像形成过程引起的层的典型形状变化的模型,我们采用联合高斯分布.2我们用NbM表示图像列j的所有边界k的连续高度值。 尺寸向量b=(b k,j)(k = 1…N,J = 1…M)。因此,
![]()
其中参数μ和∑是从标记的训练数据离线学习的。 我们通过概率主成分分析(PPCA)来规范∑的估计(Tipping和Bishop,1999)。 PPCA假设高维观测b是由一个低维潜在源s∈Rq产生的。通过
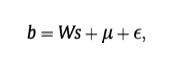
其中sN(0,1)和∈N(0,1)是各向同性高斯噪声. p(b)的矩阵由E[b] = μ和 V[b] = WW^T + σ ^2I = ∑给出。 同样,∑ ^-1也可以分解为W和σ ^2I. 利用这些分解,可以降低与∑或∑ ^-1相关的大多数操作的复杂性以及存储器要求,因为只需要存储W和σ ^2。可以通过最大对数似然估计p(b)的参数。 W由具有最大特征值的(加权的)qppca特征向量组成,从经验协方差矩阵计算。 有关详细信息,请参阅Tipping和Bishop(1999)。
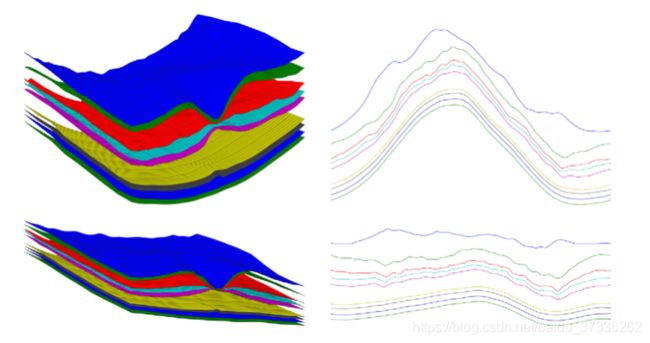
图4.由体积先验分布p(b)生成的样本在体积(左)和圆形扫描(右)上训练。 仅显示了一半的体积
图4显示了从p(b)绘制的样本,建立了以中心凹为中心的3-D体积(左)和圆形扫描(右)。 另外,作为补充材料,我们提供视频,其可视化W的每个组件的相关性,用于3-D设置,例如平移,旋转,层的厚度或中央凹的位置和形式。
2.4形状诱导的正则化器
我们模型的第三个组成部分包括离散边界分配的先验c,规范数据似然项p(y|c)。我们将p(c|b)定义为列式非循环图
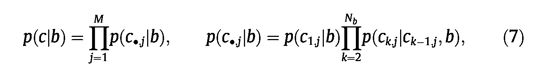
即,图像列j之间的模型的通信由形状先验p(b)控制。
为了定义(7)中的条件边界,我们需要一些先决条件。使用b.\j表示删除变量b.j后的j列b的变量子集,列j的 j,以及p(b.j|b.\j)表示从形状先验p(b)计算的相应条件高斯分布,然后边际分布用b表示通过
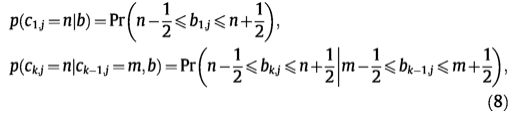
其中右侧的概率分别使用条件边际密度p(b1,j|b.,\j)和p(bk,j|b.,\j)p(bk,j|bk-1,j)计算,对于符合(2)的c的所有配置。边缘p(bk,j|b.,\j)提供了一种将全局形状知识引入我们的列式图形模型p(c|b)的方法。
2.5二维与三维
到目前为止,我们的描述被认为是OCT扫描维数二。尽管如此,我们的方法同样适用于三维。我们使用相同的表示法,因为添加额外的B扫描只会增加图像列的数量M.类似地,图形模型p(y,c,b)的连通性可以一对一地传递。
由于∑-1密集,完全连接的形状先验p(c|b)可以扩展到任意尺寸(维度)。我们利用∑和 ∑-1都具有明确的低秩分解(参见第2.3节)这一事实,这样内存消耗不是问题,操作的复杂性也会降低。对于形状正则化项p(c|b),每个节点ck,j连接到除当前列之外的所有列的节点b\j,其现在另外包括所有其他B扫描的列。 最后,数据似然性p(y|c)继续完全分解像素(i,j)。 每个像素(i,j)保持连接到来自同一列j的至多两个节点ck,j,确定它的标签xi,j。 此外,我们为卷中的每个B扫描使用单独(独立)的外观模型集来捕获可能的变化。
3.变分推断
基于前一节中给出的模型及观测数据y,我们希望推断出后验

一个主要问题是计算边际似然p(y)需要将p(y,c,b)整合到b和c上(积分)。 事实证明这是难以处理的,因为我们缺乏封闭形式的解决方案,而且手头的问题是高维的。 我们通过应用已建立的变分方法来处理这个问题:通过最小化Kullback-Leibler(KL)距离KL(q||p)相对于q(Attias(2000))来近似于易处理的分布q(b,c)。 我们指出,与相关工作(例如McGrory等人(2009))不同,其中推断离散决策变量的子问题也必须近似,我们的模型设计为通过正确选择q,所有子问题都易于处理, 可以有效地解决。
我们选择分解近似分布

这仅仅是对整体模型的连续形状先验和离散保序分割分量进行解耦,而对两个分量进行精确表示。q与p之间的Kullback-Leibler距离由
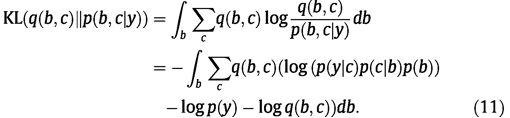
删除常数项log p(y),我们可以获得我们的目标函数。
或者,我们可以使用边际似然log p(y)将判别性外观项引入模型,使用logpðyjcÞpðylogpðyjcÞpðcÞpðylogpðclogpðcjylogpðcÞ。由于p(b)已经包含有关边界位置形状的先验知识,因此我们假设c的无信息先验。因此降低pðcÞ并考虑q的因式分解,我们得到目标函数
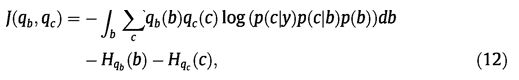
其中HpðxÞ表示分布p的熵。事实证明,有辨别力的外表术语产生了最佳表现。第5.2节将讨论这个问题。
3.1。 qc和qb的定义
对于qc©,我们采用与p(c|b)相同的因子分解,即
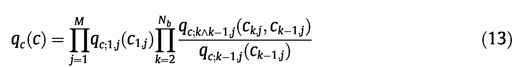
其中qckjN是离散概率分布。 类似地,通过qckk1j N2,我们表示变量对ck1,jckj上的离散概率分布。 要使qcc成为有效分布,必须满足额外的边际化约束: