李宏毅机器学习——课后作业2
文章目录
- 要求:
- 代码介绍:
-
- 1.加载库函数,设置路径
- 2.加载数据
- 3.进行数据标准化
- 4.建立模型
-
- 1.划分训练集
- 2.模型内部函数介绍
- 3.训练
- 5.完整代码:
要求:
运用逻辑回归的方法,根据性别、年龄、学历、婚姻状况、从事的行业等特征,预测居民的个人收入是否大于5万美元。
代码介绍:
1.加载库函数,设置路径
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
#添加文件路径
X_train_fpath = 'X_train'
Y_train_fpath = 'Y_train'
X_test_fpath = 'X_test'
output_fpath = 'output_{}.csv' #用于测试集的预测输出
2.加载数据
#加载数据
with open(X_train_fpath) as f:
next(f)
X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
with open(Y_train_fpath) as f:
next(f)
Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
with open(X_test_fpath) as f:
next(f)
X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
函数介绍:
该函数功能将数据去掉第一行,去掉第一列,然后按照’,'进行数据分割,并将数据类型变成float。
函数应用举例:
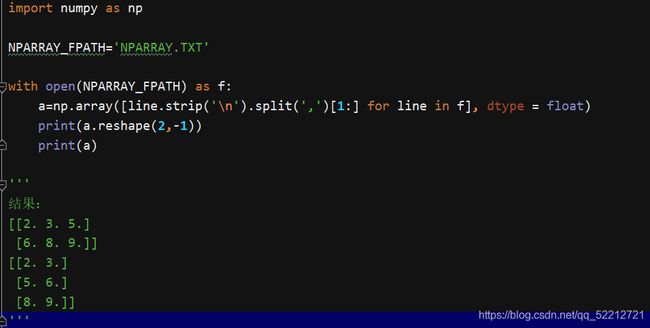
NPARRAY.txt文件如下:
1,2,3
4,5,6
7,8,9
NPARRAY.py文件如下:
import numpy as np
NPARRAY_FPATH='NPARRAY.TXT'
with open(NPARRAY_FPATH) as f:
a=np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
print(a)
结果如下:
[[2. 3.]
[5. 6.]
[8. 9.]]
加上next(f)后结果如下:
[[5. 6.]
[8. 9.]]
3.进行数据标准化
#数据标准化(Z标准化)
def _normalize(X, train = True, specified_column = None, X_mean = None, X_std = None):
# 参数:
# X: 需要标准化的数据
# train: 处理training data时为'True',处理testing data时为‘False'.
# specific_column: 数据中需要标准化的列(feature),所有列都需要标准化时为None
# X_mean:数据的均值
# X_std: 数据的标准差
# 结果:
# X: 标准化后的数据
# X_mean:数据的均值
# X_std: 数据的标准差
if specified_column == None:
specified_column = np.arange(X.shape[1])
if train:
X_mean = np.mean(X[:, specified_column] ,0).reshape(1, -1)
X_std = np.std(X[:, specified_column], 0).reshape(1, -1)
X[:,specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)
return X, X_mean, X_std
X_train, X_mean, X_std = _normalize(X_train, train = True)
X_test, _, _= _normalize(X_test, train = False, specified_column = None, X_mean = X_mean, X_std = X_std)
函数介绍:
- Z标准化:

图片来源于:数据规范化(归一化)、及Z-score标准化 - shape函数
函数功能:读取矩阵长度
函数举例:
- reshape函数:
函数功能:
1.当原始数组A[4,6]为二维数组,代表4行6列。
A.reshape(-1,8):表示将数组转换成8列的数组,具体多少行我们不知道,所以参数设为-1。用我们的数学可以计算出是3行8列
2当原始数组A[4,6]为二维数组,代表4行6列。
A.reshape(3,-1):表示将数组转换成3行的数组,具体多少列我们不知道,所以参数设为-1。用我们的数学可以计算出是3行8列
reshape函数不会改变原数组
函数举例:
- arange函数
函数功能:返回一个等差数组
函数举例:如因为X.shape[1]=510,所以specified_column是一个[0,1,…509]的数组 - mean函数
numpy.mean(a, axis, dtype, out,keepdims )
mean()函数功能:求取均值
经常操作的参数为axis,以m * n矩阵举例:
axis 不设置值,对 mn 个数求均值,返回一个实数
axis = 0:压缩行,对各列求均值,返回 1 n 矩阵
axis =1 :压缩列,对各行求均值,返回 m *1 矩阵 - std函数
numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)
这个函数是用来求标准差的。
axis=0时,表示求每一列标准差,axis=1时,表示求每一行标准差,当axis=None时,表示求全局标准差。
其次numpy计算的为总体标准偏差,即当ddof=0时,计算有偏样本标准差;一般在拥有所有数据的情况下,计算所有数据的标准差时使用,即最终除以n。
当ddo = 1时,表示计算无偏样本标准差,最终除以n-1
函数举例:
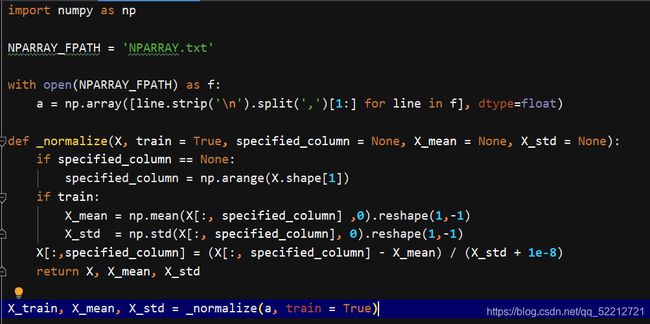
X_train结果:
[[-1.22474487 -1.22474487]
[ 0. 0. ]
[ 1.22474487 1.22474487]]
X_mean结果:
[[5. 6.]]
结果解释:(2+5+8)/3,(3+6+9)/3,计算每一列的均值
X_std结果:
[[2.44948974 2.44948974]]
结果解释:
根号下[ ( (2-5)**2+(5-5)**2+(8-5)**2 )/3 ]=根号6
根号下[ ( (3-6)**2+(6-6)**2+(9-6)**2 )/3 ]=根号6
基本上将整个函数给讲解了一遍,但是还有一个地方不太明白,为什么要X[:,specified_column]?有个地方说是因为为每个数据添加索值,不是特别懂,所以,如果有懂的朋友麻烦在评论中告诉我一声。(个人理解见下文_shuffle函数)
4.建立模型
1.划分训练集
training set:训练集是用来训练模型的。遵循训练集大,开发,测试集小的特点,占了所有数据的绝大部分。
development set:用来对训练集训练出来的模型进行测试,通过测试结果来不断地优化模型。
#分割训练集-验证集
def _train_dev_split(X, Y, dev_ratio = 0.25):
# This function spilts data into training set and development set.
train_size = int(len(X) * (1 - dev_ratio))
return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]
# 设置训练集-验证集
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio = dev_ratio)
train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]
print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))
2.模型内部函数介绍
_shuffle(X, Y)函数:
#打乱数据顺序,重新为minibatch分配
def _shuffle(X, Y):
# This function shuffles two equal-length list/array, X and Y, together.
randomize = np.arange(len(X))
np.random.shuffle(randomize)
return (X[randomize], Y[randomize])
什么是mini batch
我们已知在梯度下降中需要对所有样本进行处理,那么如果我们的样本规模的特别大的话效率就会比较低。假如有500万,甚至5000万个样本(在我们的业务场景中,一般有几千万行,有些大数据有10亿行)的话走一轮迭代就会非常的耗时。这个时候的梯度下降叫做full batch。
所以为了提高效率,我们可以把样本分成等量的子集。 例如我们把100万样本分成1000份, 每份1000个样本, 这些子集就称为mini batch。然后我们分别用一个for循环遍历这1000个子集。 针对每一个子集做一次梯度下降。 然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。
我们将遍历一次所有样本的行为叫做一个 epoch,也就是一个世代。 在mini batch下的梯度下降中做的事情其实跟full batch一样,只不过我们训练的数据不再是所有的样本,而是一个个的子集。 这样在mini batch我们在一个epoch中就能进行1000次的梯度下降,而在full batch中只有一次。 这样就大大的提高了我们算法的运行速度。
mini batch的效果:
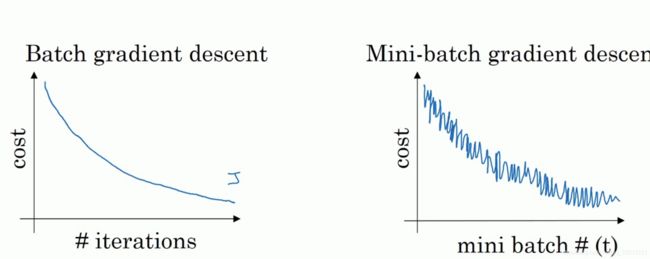
图片来源于:minibatch
函数作用:按行进行随机排列
而在这个函数当中使用了randomize,类似于上文提到的specile_conlume。
举例说明:
import numpy as np
NPARRAY_FPATH = 'NPARRAY.txt'
with open(NPARRAY_FPATH) as f:
a = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)
def _normalize(X, train=True, conlume=None, X_mean=None, X_std=None):
if conlume == None:
conlume = np.arange(X.shape[1])
if train:
X_mean = np.mean(X[:, conlume], 0).reshape(1, -1)
X_std = np.std(X[:, conlume], 0).reshape(1, -1)
X[:, conlume] = (X[:, conlume] - X_mean) / (X_std + 1e-8)
return X, X_mean, X_std
def _shuffle(X,Y):
randomize=np.arange(len(X))
np.random.shuffle(randomize)
return (X[randomize],Y[randomize])
b,c=_shuffle(a,a)
print(b)
print(c)
运行上述代码,会发现输出为:

感觉这就是给元素加索引的表现。
sigmoid函数:
def _sigmoid(z):
# Sigmoid function can be used to calculate probability.
# To avoid overflow, minimum/maximum output value is set.
return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))
向前传播函数:
调用sigmod函数计算前向传播值
def _f(X, w, b):
return _sigmoid(np.matmul(X, w) + b)
解释如下:
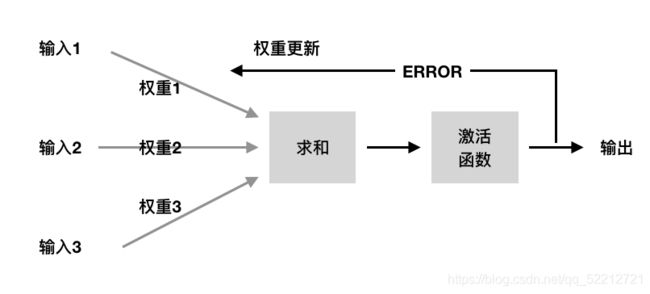
图片中的输入1、2、3便是X,只不过我们程序中的X使用的是矩阵表示,同理,权重1、2、3是w,也是使用矩阵表示。在求和阶段一般要加一个常数b,然后经过激活函数,得到一个输出。个人表述能力有限,不太懂的话推荐看一下李宏毅老师的视频课。
预测函数:
#预测
def _predict(X, w, b):
return np.round(_f(X, w, b)).astype(np.int)
使用sigmod进行一个分类,四舍五入,小于0.5是0,大于0.5是1,是否属于某个类。
交叉熵损失函数:
#交叉熵损失函数
def _cross_entropy_loss(y_pred, Y_label):
cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
return cross_entropy
交叉熵损失函数,其实就是损失函数。类似于线性回归中loss=∑(y-y^)**2,之所以在logistic Regresion中不使用loss函数而使用交叉熵,是因为在逻辑回归中我们使用的model set 是φ(wxi+b),是类伯努利模型(不知道这样说对不对),存在一个梯度消失的问题。
计算梯度函数:
def _gradient(X, Y_label, w, b):
# This function computes the gradient of cross entropy loss with respect to weight w and bias b.
y_pred = _f(X, w, b)
pred_error = Y_label - y_pred
w_grad = -np.sum(pred_error * X.T, 1)
b_grad = -np.sum(pred_error)
return w_grad, b_grad
计算交叉熵的梯度,并进行参数更新。
3.训练
接下来的这些便是使用前面一些函数进行组合,并利用一些比如参数更新公式来更新参数,应该还是比较容易懂的.
# 将w和b初始化为0
w = np.zeros((data_dim,))
b = np.zeros((1,))
# 设置其他超参数(迭代次数,分批次大小,学习率)
max_iter = 10
batch_size = 8
learning_rate = 0.2
# 创建列表用来保存训练集和验证集的损失值和准确度
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []
# 用来更新学习率
step = 1
# 训练
for epoch in range(max_iter):
# 每个epoch都会重新洗牌
X_train, Y_train = _shuffle(X_train, Y_train)
# 分批次训练
for idx in range(int(np.floor(train_size / batch_size))):
X = X_train[idx * batch_size:(idx + 1) * batch_size]
Y = Y_train[idx * batch_size:(idx + 1) * batch_size]
# 计算梯度值
w_grad, b_grad = _gradient(X, Y, w, b)
# 更新参数w和b
# 学习率随着迭代时间增加而减少
w = w - learning_rate / np.sqrt(step) * w_grad
b = b - learning_rate / np.sqrt(step) * b_grad
step = step + 1
# 参数总共更新了max_iter × (train_size/batch_size)次
# 计算训练集的损失值和准确度
y_train_pred = _f(X_train, w, b)
Y_train_pred = np.round(y_train_pred)
train_acc.append(_accuracy(Y_train_pred, Y_train))
train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)
# 计算验证集的损失值和准确度
y_dev_pred = _f(X_dev, w, b)
Y_dev_pred = np.round(y_dev_pred)
dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)
print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))
5.完整代码:
import numpy as np
import matplotlib.pyplot as plt
#确保跟博主生成相同的随机数
np.random.seed(0)
#添加文件路径
X_train_fpath = 'X_train'
Y_train_fpath = 'Y_train'
X_test_fpath = 'X_test'
output_fpath = 'output_{}.csv' #用于测试集的预测输出
#加载数据
with open(X_train_fpath) as f:
next(f)
X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
with open(Y_train_fpath) as f:
next(f)
Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype = float)
with open(X_test_fpath) as f:
next(f)
X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype = float)
#归一化
def _normalize(X, train = True, specified_column = None, X_mean = None, X_std = None):
if specified_column == None:
#为每个数据添加索值
specified_column = np.arange(X.shape[1])
if train:
#求取每个数据的平均值和标准差
X_mean = np.mean(X[:, specified_column] ,0).reshape(1,-1)
X_std = np.std(X[:, specified_column], 0).reshape(1,-1)
#归一化数据
X[:,specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)
#返回归一化后的数据,均值,标准差
return X, X_mean, X_std
# 归一化数据
X_train, X_mean, X_std = _normalize(X_train, train = True)
X_test, _, _= _normalize(X_test, train = False, specified_column = None, X_mean = X_mean, X_std = X_std)
#分割训练集-验证集
def _train_dev_split(X, Y, dev_ratio = 0.25):
# This function spilts data into training set and development set.
train_size = int(len(X) * (1 - dev_ratio))
return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]
# 设置训练集-验证集
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio = dev_ratio)
train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]
print('Size of training set: {}'.format(train_size))
print('Size of development set: {}'.format(dev_size))
print('Size of testing set: {}'.format(test_size))
print('Dimension of data: {}'.format(data_dim))
#打乱数据顺序,重新为minibatch分配
def _shuffle(X, Y):
# This function shuffles two equal-length list/array, X and Y, together.
randomize = np.arange(len(X))
np.random.shuffle(randomize)
return (X[randomize], Y[randomize])
#sigmoid函数
def _sigmoid(z):
# Sigmoid function can be used to calculate probability.
# To avoid overflow, minimum/maximum output value is set.
return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))
#向前传播然后利用sigmoid激活函数计算激活值
def _f(X, w, b):
return _sigmoid(np.matmul(X, w) + b)
#预测
def _predict(X, w, b):
return np.round(_f(X, w, b)).astype(np.int)
#准确度
def _accuracy(Y_pred, Y_label):
acc = 1 - np.mean(np.abs(Y_pred - Y_label))
return acc
#交叉熵损失函数
def _cross_entropy_loss(y_pred, Y_label):
cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
return cross_entropy
#计算梯度值
def _gradient(X, Y_label, w, b):
# This function computes the gradient of cross entropy loss with respect to weight w and bias b.
y_pred = _f(X, w, b)
pred_error = Y_label - y_pred
w_grad = -np.sum(pred_error * X.T, 1)
b_grad = -np.sum(pred_error)
return w_grad, b_grad
# 将w和b初始化为0
w = np.zeros((data_dim,))
b = np.zeros((1,))
# 设置其他超参数(迭代次数,分批次大小,学习率)
max_iter = 10
batch_size = 8
learning_rate = 0.2
# 创建列表用来保存训练集和验证集的损失值和准确度
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []
# 用来更新学习率
step = 1
# 训练
for epoch in range(max_iter):
# 每个epoch都会重新洗牌
X_train, Y_train = _shuffle(X_train, Y_train)
# 分批次训练
for idx in range(int(np.floor(train_size / batch_size))):
X = X_train[idx * batch_size:(idx + 1) * batch_size]
Y = Y_train[idx * batch_size:(idx + 1) * batch_size]
# 计算梯度值
w_grad, b_grad = _gradient(X, Y, w, b)
# 更新参数w和b
# 学习率随着迭代时间增加而减少
w = w - learning_rate / np.sqrt(step) * w_grad
b = b - learning_rate / np.sqrt(step) * b_grad
step = step + 1
# 参数总共更新了max_iter × (train_size/batch_size)次
# 计算训练集的损失值和准确度
y_train_pred = _f(X_train, w, b)
Y_train_pred = np.round(y_train_pred)
train_acc.append(_accuracy(Y_train_pred, Y_train))
train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)
# 计算验证集的损失值和准确度
y_dev_pred = _f(X_dev, w, b)
Y_dev_pred = np.round(y_dev_pred)
dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)
print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))
plt.plot(train_loss)
plt.plot(dev_loss)
plt.title('Loss')
plt.legend(['train', 'dev'])
plt.savefig('loss.png')
plt.show()
# Accuracy curve
plt.plot(train_acc)
plt.plot(dev_acc)
plt.title('Accuracy')
plt.legend(['train', 'dev'])
plt.savefig('acc.png')
plt.show()

