中科大-凸优化 笔记(lec25)-等价变换
全部笔记的汇总贴(视频也有传送门):中科大-凸优化
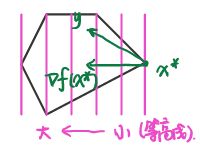
∇ f T ( x ∗ ) ( y − x ) ≥ 0 \nabla f^T(x^*)(y-x)\ge0 ∇fT(x∗)(y−x)≥0线性规划的解在边界上
一、等价变换
例:食谱问题
选择食谱,使得 m m m种营养元素分别不小于 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm
有 n n n种食物,单位食物营养为 a 1 j , a 2 j , ⋯ , a m j , ∀ j = 1 , ⋯ , n a_{1j},a_{2j},\cdots,a_{mj},\forall j=1,\cdots,n a1j,a2j,⋯,amj,∀j=1,⋯,n
目标:单位食物价格 C j C_j Cj,找出总价最小的食谱
设食物量分别为 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn
m i n ∑ j = 1 n C j x j s . t . ∑ j = 1 m C i j x j ≥ b j , i = 1 , ⋯ , m , x j ≥ 0 , j = 1 , ⋯ , n min\;\;\sum_{j=1}^nC_jx_j\\s.t.\;\;\sum_{j=1}^m C_{ij}x_j\ge b_j,i=1,\cdots,m,x_j\ge0,j=1,\cdots,n minj=1∑nCjxjs.t.j=1∑mCijxj≥bj,i=1,⋯,m,xj≥0,j=1,⋯,n
m i n [ C 1 , ⋯ , C n ] [ x 1 ⋮ x n ] s . t . [ a 11 ⋯ a 1 n ⋮ ⋮ a m 1 ⋯ a m n ] [ x 1 ⋮ x n ] = [ b 1 ⋮ b m ] , [ x 1 ⋮ x n ] ≥ 0 min\;\;[C_1,\cdots,C_n]\left[ \begin{array}{c}x_1\\\vdots\\x_n\end{array} \right] \\s.t.\left[ \begin{array}{c} a_{11}\cdots a_{1n}\\\vdots\;\;\;\;\;\;\;\;\;\vdots \\a_{m1}\cdots a_{mn} \end{array} \right]\left[ \begin{array}{c} x_1\\\vdots \\x_n \end{array} \right]=\left[ \begin{array}{c} b_1\\\vdots \\b_m \end{array} \right],\left[ \begin{array}{c} x_1\\\vdots \\x_n \end{array} \right]\ge0 min[C1,⋯,Cn]⎣⎢⎡x1⋮xn⎦⎥⎤s.t.⎣⎢⎡a11⋯a1n⋮⋮am1⋯amn⎦⎥⎤⎣⎢⎡x1⋮xn⎦⎥⎤=⎣⎢⎡b1⋮bm⎦⎥⎤,⎣⎢⎡x1⋮xn⎦⎥⎤≥0
例:线性分数规划(linear fractional programing)
( P 0 P_0 P0) min f 0 ( x ) \min f_0(x) minf0(x)线性分数函数(凸×拟凸√) f 0 ( x ) = C T x + d e T x + f d o m f 0 = { x ∣ e T x + f > 0 } f_0(x)=\frac{C^Tx+d}{e^Tx+f}\;dom\;f_0=\{x|e^Tx+f>0\} f0(x)=eTx+fCTx+ddomf0={ x∣eTx+f>0}
s . t . G x ≤ h , A x = b s.t.\;\;Gx\le h,Ax=b s.t.Gx≤h,Ax=b
不是标准的凸问题,需要转化
⇒ ( P 1 ) \Rightarrow(P_1) ⇒(P1)
min C T y + d z \min C^Ty+dz minCTy+dz
s . t . G y − h z ≤ 0 , e T x + f z = 1 , A y − b z = 0 , z ≥ 0 ( z > 0 等 价 ) s.t.\;Gy-hz\le0,e^Tx+fz=1,Ay-bz=0,z\ge0(z>0等价) s.t.Gy−hz≤0,eTx+fz=1,Ay−bz=0,z≥0(z>0等价)
证明
(1)若 x x x在 P 0 P_0 P0可行, y = x e T x + f , z = = 1 e T x + f y=\frac x{e^Tx+f},z==\frac 1{e^Tx+f} y=eTx+fx,z==eTx+f1
{ G x ≤ h A x = b e T x + f > 0 \left\{ \begin{array}{l} Gx\le h \\ Ax=b \\ e^Tx+f>0 \end{array} \right. ⎩⎨⎧Gx≤hAx=beTx+f>0
G y − h z = G x − h e T + f ≤ 0 , e T x + f z = e T x + f e T x + f = 1 , A y − b z = A x − b e T x + f = 0 z ≤ 0 Gy-hz=\frac{Gx-h}{e^T+f}\le0,e^Tx+fz=\frac{e^Tx+f}{e^Tx+f}=1,Ay-bz=\frac{Ax-b}{e^Tx+f}=0\;\;z\le0 Gy−hz=eT+fGx−h≤0,eTx+fz=eTx+feTx+f=1,Ay−bz=eTx+fAx−b=0z≤0
c T y + d z = c T x + d e T x + f = f 0 ( x ) c^Ty+dz=\frac{c^Tx+d}{e^Tx+f}=f_0(x) cTy+dz=eTx+fcTx+d=f0(x)
(2)若 y , z y,z y,z在 P 1 P_1 P1种可行,若 z > 0 z>0 z>0,则 x = y z x=\frac yz x=zy,则 x x x在 P 0 P_0 P0中可行且两问题目标函数值相同。
(3)(在下一小结将,笔记也做在这里算了)
若 y , z y,z y,z在 P 1 P_1 P1中可行,若 z = 0 z=0 z=0,设 x 0 x_0 x0为 P 0 P_0 P0的可行解
则 x = x 0 + t y x=x_0+ty x=x0+ty对 P 0 P_0 P0可行, ∀ t ≥ 0 \forall t\ge0 ∀t≥0
G y ≤ 0 , A y = 0 , e T y = 1 G x = G x 0 + G y ≤ h A x = A x 0 + t A h = b e T x + f = e T x 0 + f + t e T y > 0 f 0 ( x ) = f 0 ( x 0 + t y ) = C T x 0 + C T t y + d e T x 0 + e T y + f = ( t → ∞ ) C T y Gy\le0,Ay=0,e^Ty=1\\Gx=Gx_0+Gy\le h\\Ax=Ax_0+tAh=b\\e^Tx+f=e^Tx_0+f+te^Ty>0\\f_0(x)=f_0(x_0+ty)=\frac{C^Tx_0+C^Tty+d}{e^Tx_0+e^Ty+f}=(t\rightarrow \infty)C^Ty Gy≤0,Ay=0,eTy=1Gx=Gx0+Gy≤hAx=Ax0+tAh=beTx+f=eTx0+f+teTy>0f0(x)=f0(x0+ty)=eTx0+eTy+fCTx0+CTty+d=(t→∞)CTy
下一章传送门:中科大-凸优化 笔记(lec26)-二次规划