数据挖掘-数据离散化 python实现

数据挖掘-数据离散化 python实现

# -*-coding:utf-8-*-

"""
    Author: Thinkgamer
    Desc:
        代码4-2  基于信息熵的数据离散化
"""
import numpy as np
import math

class DiscreteByEntropy:
    def __init__(self, group, threshold):
        self.maxGroup = group  # 最大分组数
        self.minInfoThreshold = threshold  # 停止划分的最小熵
        self.result = dict()  # 保存划分结果

    # 准备数据
    def loadData(self):
        data = np.array(
            [
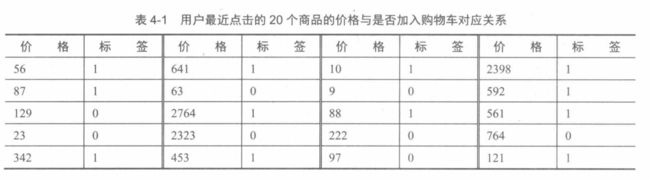
                [56, 1],   [87, 1],  [129, 0],  [23, 0],   [342, 1],
                [641, 1],  [63, 0],  [2764, 1], [2323, 0], [453, 1],
                [10, 1],   [9, 0],   [88, 1],   [222, 0],  [97, 0],
                [2398, 1], [592, 1], [561, 1],  [764, 0],  [121, 1],
            ]
        )
        return data

    # 计算按照数据指定数据分组后的香农熵
    def calEntropy(self, data):
        numData = len(data)
        labelCounts = {
     }
        for feature in data:
            # 获得标签
            oneLabel = feature[-1]
            # 如果标签不在新定义的字典里创建该标签值
            labelCounts.setdefault(oneLabel, 0)
            # 该类标签下含有数据的个数
            labelCounts[oneLabel] += 1
        shannonEnt = 0.0
        for key in labelCounts:
            # 同类标签出现的概率
            prob = float(labelCounts[key]) / numData
            # 以2为底求对数
            shannonEnt -= prob * math.log(prob, 2)
        return shannonEnt

    # 按照调和信息熵最小化原则分割数据集
    def split(self, data):
        # inf为正无穷大
        minEntropy = np.inf
        # 记录最终分割索引
        index = -1
        # 按照第一列对数据进行升序排序
        sortData = data[np.argsort(data[:, 0])]
        # 初始化最终分割数据后的熵
        lastE1, lastE2 = -1, -1
        # 返回的数据结构，包含数据和对应的熵
        S1 = dict()
        S2 = dict()
        for i in range(len(sortData)):
            # 分割数据集
            splitData1, splitData2 = sortData[: i + 1], sortData[i + 1 :]
            entropy1, entropy2 = (
                self.calEntropy(splitData1),
                self.calEntropy(splitData2),
            )  # 计算信息熵
            entropy = entropy1 * len(splitData1) / len(sortData) + \
                      entropy2 * len( splitData2) / len(sortData)
            # 如果调和平均熵小于最小值
            if entropy < minEntropy:
                minEntropy = entropy
                index = i
                lastE1 = entropy1
                lastE2 = entropy2
        S1["entropy"] = lastE1
        S1["data"] = sortData[: index + 1]
        S2["entropy"] = lastE2
        S2["data"] = sortData[index + 1 :]
        return S1, S2, entropy

    # 对数据进行分组
    def train(self, data):
        # 需要遍历的key
        needSplitKey = [0]
        # 将整个数据作为一组
        self.result.setdefault(0, {
     })
        self.result[0]["entropy"] = np.inf
        self.result[0]["data"] = data
        group = 1
        for key in needSplitKey:
            S1, S2, entropy = self.split(self.result[key]["data"])
            # 如果满足条件
            if entropy > self.minInfoThreshold and group < self.maxGroup:
                self.result[key] = S1
                newKey = max(self.result.keys()) + 1
                self.result[newKey] = S2
                needSplitKey.extend([key])
                needSplitKey.extend([newKey])
                group += 1
            else:
                break

if __name__ == "__main__":
    dbe = DiscreteByEntropy(group=6, threshold=0.5)
    data = dbe.loadData()
    dbe.train(data)
    print("result is {}".format(dbe.result))

• 结果

result is {
     0: {
     'entropy': 0.0, 'data': array([[9, 0]])}, 1: {
     'entropy': 0.0, 'data': array([[342,   1],
       [453,   1],
       [561,   1],
       [592,   1],
       [641,   1]])}, 2: {
     'entropy': 0.0, 'data': array([[129,   0],
       [222,   0]])}, 3: {
     'entropy': 1.0, 'data': array([[ 764,    0],
       [2323,    0],
       [2398,    1],
       [2764,    1]])}, 4: {
     'entropy': 0.9544340029249649, 'data': array([[ 10,   1],
       [ 23,   0],
       [ 56,   1],
       [ 63,   0],
       [ 87,   1],
       [ 88,   1],
       [ 97,   0],
       [121,   1]])}}

Process finished with exit code 0