基于深度优先算法实现的超高速的机器人未知环境（迷宫）探索，以及基于广度优先算法实现的最短路径搜索

这个项目其实是我的一项课后作业，经过一段时间的努力完成之后，颇有一番收获，所以在此分享，如有不对之处还请各位批评指正！

还有这个程序是用纯C编写的，所以在visual studio上运行起来可能会有一点问题，大家在codeblocks或Dev上运行就没问题了

考虑一个简单的移动机器人，它能够在平面上沿着可以行走的路径移动，并能够记录自身的运行轨迹。为简化问题，假定在每一个地点，机器人移动的方向只能是前、后、左、右、右前、右后、左前和左后八个方向，而且也只能感知到其周围局部八个位置的信息(是可行路径、不可达区域还是目标点)。

#include 
#include 
#include 
#include 
#include 
#include   //这里是为了导入音乐而设置的
#pragma comment(lib, "winmm.lib")  //这里是为了导入音乐而设置的
#define N 10000
#define row 55
#define colume 177
int min = 99999, target = 0, important_target = 0, g = 0, color = 10, speed, counter = 1, FLAG = 0, flag = 0, p = 0, q = 0, signal = 0, tx, ty, h, u;
int dir[8][2] = {
     {
     0, 1}, {
     1, 1}, {
     1, 0}, {
     1, -1}, {
     0, -1}, {
     -1, -1}, {
     -1, 0}, {
     -1, 1}};  //8个方向
int a[row][colume] = {
     0}, v[row][colume] = {
     0}, r[row][colume] = {
     0}, s[row][colume] = {
     0}, z[N][2] = {
     0}, mem[N][3];  //0表示未访问，1表示访问
long cstart,cends;
struct node  //定义了一个结构体用于实现顺序队列
{
     
    int x,y;
    int pre;
}que[10000];
void store(int s)  //存储坐标点
{
     
    if(que[s].pre!=-1)
    {
     
        store(que[s].pre);    //这里的递归非常精巧，可以实现对于路径的回溯，从而节省了几十行的代码量，实现逆序输出
        mem[signal][0] = que[s].x;
        mem[signal][1] = que[s].y;
        mem[signal][2] = que[s].pre;
        signal++;
    }
}
void bfs(int x,int y)  //广度优先搜索算法
{
     
    int head=1,tail=1;
    que[tail].x=x;  //定义的x，y坐标
    que[tail].y=y;
    que[tail].pre=-1;  //用于回溯的一个登记值
    tail++;
    while(head<tail)
    {
     
        for(int i=0;i<8;i++)
        {
     
            tx = que[head].x + dir[i][0];
            ty = que[head].y + dir[i][1];
            if(tx < 0 || tx >= row || ty<0 || ty >= colume)  //避免超出边界
            {
     
                continue;
            }
            if ((a[tx][ty] == 0 || a[tx][ty] == 2 || a[tx][ty] == 3 || a[tx][ty] == 4) && v[tx][ty] == 0)  //通过一个二维数组的遍历来实现8个方向的搜索
            {
     
            	if(a[tx][ty] == 3)
				{
     
					r[tx][ty] = 3;
				}
                v[tx][ty]=1;
                que[tail].x=tx;
                que[tail].y=ty;
                que[tail].pre=head;
                tail++;
            }
            if(tx==p&&ty==q)  //如果到达终点，就调用store函数来存储坐标值
            {
     
                store(head);
            }
        }
        head++;
    }
}
void Change()  //根据实际搜索到的数值来改变r数组中存储的路线图，进而在后面呈现最短路径
{
     
    int i;
    for(i=0;i<N;i++)
    {
     
        if(mem[i-1][2] > mem[i][2])
        {
     
            break;
        }
        switch(a[mem[i][0]][mem[i][1]])
		{
     
		case 0:
			r[mem[i][0]][mem[i][1]] = 4;
			break;
		case 2:
			r[mem[i][0]][mem[i][1]] = 2;
			break;
		case 3:
			r[mem[i][0]][mem[i][1]] = 3;
			break;
		}
        if(a[mem[i][0]][mem[i][1]] == 3)  //跳过后面修改该处的点为4，进而显示路径的操作，避免程序修改了必达点的数值，导致必达点的标记不可见
		{
     
			continue;
		}
        a[mem[i][0]][mem[i][1]] = 4;
        if (counter % speed == 0)  //通过确定一个标志值来设置探索的速度
		{
     
			system("cls");
			Show(a, row, colume);
		}
		counter++;
		if (counter == 10001)  //避免counter变量过大而溢出
		{
     
			counter = 1;
		}
    }
    signal = 0;  //该函数执行完毕后初始化，便于进行下一步探索新的点
    memset(v, 0, sizeof(v));
    memset(mem, 0, sizeof(mem));
    memset(que, 0, sizeof(que));
}
void ShortBFS()  //最短路径总函数，第一次设置第一个点为起点，最近的一个点为终点，探索他们之间的最短路径；第二次设置最近的那个点为起点，第二近的点为终点，探索他们之间的最短路径，依次循环执行···
{
     
	int i;
	h = 1;  //初始化起点
	u = 1;
	for (i = 0; i < important_target; i++)
	{
     
		p = z[i][0];  //设置终点，后面每一次都修改这个终点的坐标
		q = z[i][1];
		bfs(h, u);  //在这里每一次遍历必达点后调用
		Change();
		h = p;  //以刚刚的那个终点为起点再一次开始
		u = q;
	}
}
void setcolor(int color)  //设置控制台打印输出字符颜色的函数
{
     
    HANDLE
	hc=GetStdHandle(STD_OUTPUT_HANDLE);
    SetConsoleTextAttribute(hc,0|color);
}
void WritetoFile(int s[row][colume], int n)  //将遍历后的地图与路线图写入文件，通过不同的n来决定写入那一个文件之中
{
     
	FILE *fp;
	switch(n)
	{
     
	case 0:
		if ((fp = fopen("map.txt", "w")) == NULL)
		{
     
			printf("无法打开map.txt文件！\n");
			exit(0);
		}
		break;
	case 1:
		if ((fp = fopen("全图探索路线图.txt", "w")) == NULL)
		{
     
			printf("无法打开全图探索路线图.txt文件！\n");
			exit(0);
		}
		break;
	case 2:
		if ((fp = fopen("最短路径路线图.txt", "w")) == NULL)
		{
     
			printf("无法打开最短路径路线图.txt文件！\n");
			exit(0);
		}
		break;
	}
	fwrite(s, sizeof(int), row * colume, fp);
	fclose(fp);
}
void ReadfromFile(int s[row][colume], int n)  //读出地图和路线图
{
     
	FILE *fp;
	switch(n)
	{
     
	case 0:
		if ((fp = fopen("map.txt", "r")) == NULL)
		{
     
			printf("无法打开map.txt文件！\n");
			exit(0);
		}
		break;
	case 1:
		if ((fp = fopen("全图探索路线图.txt", "r")) == NULL)
		{
     
			printf("无法打开全图探索路线图.txt文件！\n");
			exit(0);
		}
		break;
	case 2:
		if ((fp = fopen("最短路径路线图.txt", "r")) == NULL)
		{
     
			printf("无法打开最短路径路线图.txt文件！\n");
			exit(0);
		}
		break;
	}
	fread(s, sizeof(int), row * colume, fp);
	fclose(fp);
}
void dfs(int x, int y, int step, int flag)  //深度优先搜索算法
{
     
	int i;
	a[x][y] = 4;
	if (counter % speed == 0)  //决定机器人运动的速度，原理同上
	{
     
		system("cls");
		if (flag == 1)
		{
     
			Show(a, row, colume);
		}
		if (flag == 2)
		{
     
			Show(v, row, colume);
		}
		if (flag == 3)
		{
     
			Show(r, row, colume);
		}
	}
	counter++;
	if (counter == 10001)
	{
     
		counter = 1;
	}
	//顺时针试探
	for (i = 0; i < 8; i++)  //遍历八个方向
	{
     
		if ((a[x + dir[i][0]][y + dir[i][1]] == 0 || a[x + dir[i][0]][y + dir[i][1]] == 2 || a[x + dir[i][0]][y + dir[i][1]] == 3) && v[x + dir[i][0]][y + dir[i][1]] == 0)
		{
     
			switch(a[x + dir[i][0]][y + dir[i][1]])
			{
     
			case 0:
				r[x + dir[i][0]][y + dir[i][1]] = 4;
				break;
			case 2:
				r[x + dir[i][0]][y + dir[i][1]] = 2;
				target ++;
				break;
			case 3:
				r[x + dir[i][0]][y + dir[i][1]] = 3;
				important_target++;
				z[g][0] = x + dir[i][0];
				z[g][1] = y + dir[i][1];
				g++;
				break;
			}
			v[x + dir[i][0]][y + dir[i][1]] = 1;
			dfs(x + dir[i][0], y + dir[i][1], step + 1, flag);
			v[x + dir[i][0]][y + dir[i][1]] = 0;
		}
	}
	return;
}
void exchange(int important_target)  //将所存储的必达点的坐标，按照x**2 + y**2的大小来进行排序交换的函数
{
     
	int i, j, x, y, k;
	for (i = 0; i < important_target - 1; i++)
	{
     
		k = i;
		for (j = i + 1; j < important_target; j++)
		{
     
			if ( ( (z[j][0]) * (z[j][0]) + (z[j][1])*(z[j][1])) < ( (z[k][0])*(z[k][0]) + (z[k][1])*(z[k][1])) )  //实现比较x**2 + y**2的大小进而交换
			{
     
				k = j;
			}
		}
		if (k != i)
		{
     
			x = z[i][0];
			z[i][0] = z[k][0];
			z[k][0] = x;
			y = z[i][1];
			z[i][1] = z[k][1];
			z[k][1] = y;
		}
	}
}
void show_array(int important_target)  //展示排序后的必达点坐标
{
     
	int i;
	for (i = 0; i < important_target; i++)
	{
     
		printf("第%d个必达点（%-2d，%-2d）\n", i + 1, z[i][0], z[i][1]);
	}
}
void Show(int a[row][colume], int n, int m)  //将二维整型数组进行可视化输出
{
     
	int i, j;
	for (i = 0; i < n; ++i)
	{
     
		for (j = 0; j < m; ++j)
		{
     
			if (a[i][j] == 0)
			{
     
				printf(" ");
			}
			else if (a[i][j] == 1)
			{
     
				setcolor(8);
				printf("*");
			}
			else if (a[i][j] == 2)
			{
     
				setcolor(2);
				printf("@");
			}
			else if (a[i][j] == 3)
			{
     
				setcolor(4);
				printf("$");
			}
			else if (a[i][j] == 4)
			{
     
				setcolor(color);
				printf("o");
			}
		}
		printf("\n");
	}
}
void menu()  //展示初始的菜单
{
     
	setcolor(14);
	printf("欢迎来到美丽的机器人探险世界\\(￣︶￣*\\))\n\n");
	printf("(￣(工)￣)\t功能菜单\t(￣(工)￣)\n\n");
	printf("^(*￣(oo)￣)^\t1、带着地图的展示方式\t^(*￣(oo)￣)^\n\n");
	printf("(o-ωｑ)).oO 困\t2、纯路线展示方式（可以展现试探的过程哦！）\t(o-ωｑ)).oO 困\n\n");
	printf("(＠_＠;)\t3、纯路线但有着关键点的展示方式（仅路线而已，可没有试探哦！）\t(＠_＠;)\n\n");
	printf("(￣m￣)\t\t4、如果你想查看行走后的路线图，就选它吧！\t(￣m￣)\n\n");
	if (FLAG > 0)
	{
     
		printf("ε=ε=ε=(~￣▽￣)~5、显示最省能量的路径，即最短路径\tε=ε=ε=(~￣▽￣)~\n\n");
	}
	printf("(╯▽╰ )好香~~\t请选择一个你喜欢的功能吧！（如果想退出的话请输入0哦！）\t(╯▽╰ )好香~~\n\n");
}
void series()  //进行部分初始化的函数
{
     
	memset(v,0,sizeof(v));
	memset(r,0,sizeof(r));
	g = 0;
	ReadfromFile(a, 0);
}
void total(int t)  //为简化代码而编写的函数
{
     
	int startx, starty;
	series();
	memset(z,0,sizeof(z));
	important_target = 0;
	target = 0;
	setcolor(14);
	printf("请输入出发点像这样：1，1（中文输入法即可）\n");
	scanf("%d，%d", &startx, &starty);
	printf("请选择一个你喜欢的机器人颜色：蓝-1 深绿-2 浅蓝-3 红-4 紫-5 黄-6 白-7 灰-8 中蓝-9 浅绿-10 超浅蓝-11 橙红-12 浅紫-13\n");
	scanf("%d", &color);
	printf("请选择机器人的运动速度：1-1000（正常运动是很慢的哦！o(≧口≦)o）\n");
	scanf("%d", &speed);
	v[startx][starty] = 1;
	cstart = clock();
	dfs(startx, starty, 0, t);
	setcolor(14);
	cends = clock();
	printf("全图探索所耗时间为%f秒\n", (cends-cstart)/1000.0);
    system("pause");
	printf("(～￣▽￣)～呐！主人，探险后的路线图为：\n");
	system("pause");
	Show(r, row, colume);
	WritetoFile(r, 1);
	setcolor(14);
    system("pause");
	printf("探险目标点个数为：%d个，特殊重要的、必须到达的目标点个数为：%d个\n\n", target, important_target);
	printf("其中，按照由近及远的顺序，特殊重要的、必须到达的目标点的坐标为：\n");
	exchange(important_target);
	system("pause");
	show_array(important_target);
	printf("(╯▽╰ )好香~~\t请再次选择一个你喜欢的功能吧！（如果想退出的话请输入0哦！）\t(╯▽╰ )好香~~\n\n");
	menu();
}
int main()
{
     
    PlaySound("周杰伦-Mojito.wav",NULL,SND_FILENAME|SND_ASYNC|SND_LOOP);
	int n;
	menu();
	FLAG++;
	scanf("%d", &n);
	while(n != 0)
	{
     
		switch(n)  //根据用户的输入确定不同的功能
		{
     
		case 1:
			total(1);
			scanf("%d", &n);
			break;
		case 2:
			total(2);
			scanf("%d", &n);
			break;
		case 3:
			total(3);
			scanf("%d", &n);
			break;
		case 4:
			printf("( $ _ $ )\t如果是全图探索路线图请输入1， 如果是最短路径路线图请输入2\t( $ _ $ )\n");
			beg:
			getchar();
			scanf("%d", &n);
			if(n == 1)
			{
     
				ReadfromFile(r, 1);
				Show(r, row, colume);
				series();
				goto exit;
			}
			if(n == 2)
			{
     
				ReadfromFile(r, 2);
				Show(r, row, colume);
				series();
			}
			else
			{
     
				setcolor(14);
				printf("可没有这个功能号哦！请仔细检查！(╬▔皿▔)凸 我可有点生气了，请再输入一个正确的功能号吧！\n");
				getchar();
				scanf("%d", &n);
				goto beg;
			}
			exit:
			setcolor(14);
			printf("(╯▽╰ )好香~~\t请再次选择一个你喜欢的功能吧！（如果想退出的话请输入0哦！）\t(╯▽╰ )好香~~\n\n");
			menu();
			scanf("%d", &n);
			break;
		case 5:  //增加了保存路径的程序，可对走过的路线进行保存
			series();
			printf("请选择机器人的运动速度：1-1000（正常运动是很慢的哦！o(≧口≦)o）\n");
			scanf("%d", &speed);
			cstart = clock();
			ShortBFS();
			cends = clock();
			setcolor(14);
			printf("最短路径探索所耗时间为%f秒！\n", (cends-cstart)/1000.0);
			system("pause");
			printf("走完了，好累呀！\n");
			printf("(～￣▽￣)～呐！主人，最节省能量的路径为：\n");
			Show(r, row, colume);
			WritetoFile(r, 2);
            setcolor(14);
            system("pause");
			printf("(╯▽╰ )好香~~\t请再次选择一个你喜欢的功能吧！（如果想退出的话请输入0哦！）\t(╯▽╰ )好香~~\n\n");
			menu();
			scanf("%d", &n);
			break;
		}
		while(n >= 6 || n < 0)  //防止用户输入错误
		{
     
			setcolor(14);
			printf("可没有这个功能号哦！请仔细检查！(╬▔皿▔)凸 我可有点生气了，请再输入一个正确的功能号吧！\n");
			getchar();
			scanf("%d", &n);
		}
	}
	setcolor(14);
	printf("退出成功了呢！谢谢您的使用！下次再见吧！(∪.∪ )...zzz\n");
	system("PAUSE");
}

首先，本程序结合了深度优先搜索与广度优先搜索两种算法，前者用来实现机器人的可视化动态探索，后者用来实现最短路径的寻找，充分利用了深度优先探索可以最大程度可视化模拟机器人探索过程的优点，与广度优先算法对于大型地图仍保有超高计算速度的优点，克服了深度优先算法的时间复杂度高的问题，同时兼顾了广度优先算法空间复杂度高的问题，通过二者的完美融合得到了目前状态下机器人探索问题的最优解。
其次，关于最短路径问题，首先，通过第一次探索全图来获知所有的必达点的坐标，然后将这些点根据与坐标原点之间的绝对距离大小，按从小到大进行排序，将其存储到一个数组中，最后第二次探索时，首先以原点为出发点，以数组中存储的第一近的点为终点，通过广度优先搜索算法来找到它们之间的最短路径，并可视化的通过“走”展现出来。然后，根据之前所存储的数组中第一近的点为起点，以第二近的点为终点，搜索它们之间的最短路径，并可视化的通过“走”展现出来······最后，将这个整个过程中的所有的最短路径加起来，得到总的最短路径，并在后面打印出来。
最后在程序代码编写上，我力求简洁，并通过各种方式极大简化了代码，在不影响功能与代码的简洁美观性的基础上，将代码压缩至457行。在人性化方面，尽管是单调的控制台界面，但我尽可能的添加了一些可爱的表情符号，在最大程度上改善用户的使用体验，我并没有采用题中推荐的字符数组，而是采用了整形数组来存储地图，然后在打印输出时转化为符号进行输出。这样有两个好处，其一是在编辑地图时，由于数字的大小都是一样的，所以在编辑的过程中，我们所看到的和最后所打印出来的地图在位置上是一样的，这就给编辑地图工作带来了很多便利；其二是，整形数组不会出现，像“\0”这样的字符串结束符干扰程序的判断，还可以减少许多潜在的读取的bug。同时由于电脑屏幕显示行数有限的原因，我并没有采用100100的数组，而是采用55177的数组来表示地图，这个大小正好可以在控制台全屏显示，从而比较好的解决了因为电脑自动滚动翻页而引发地图在控制台上晃来晃去无法显示的问题，并且本程序提供了三种动态探索形式，它们分别是：
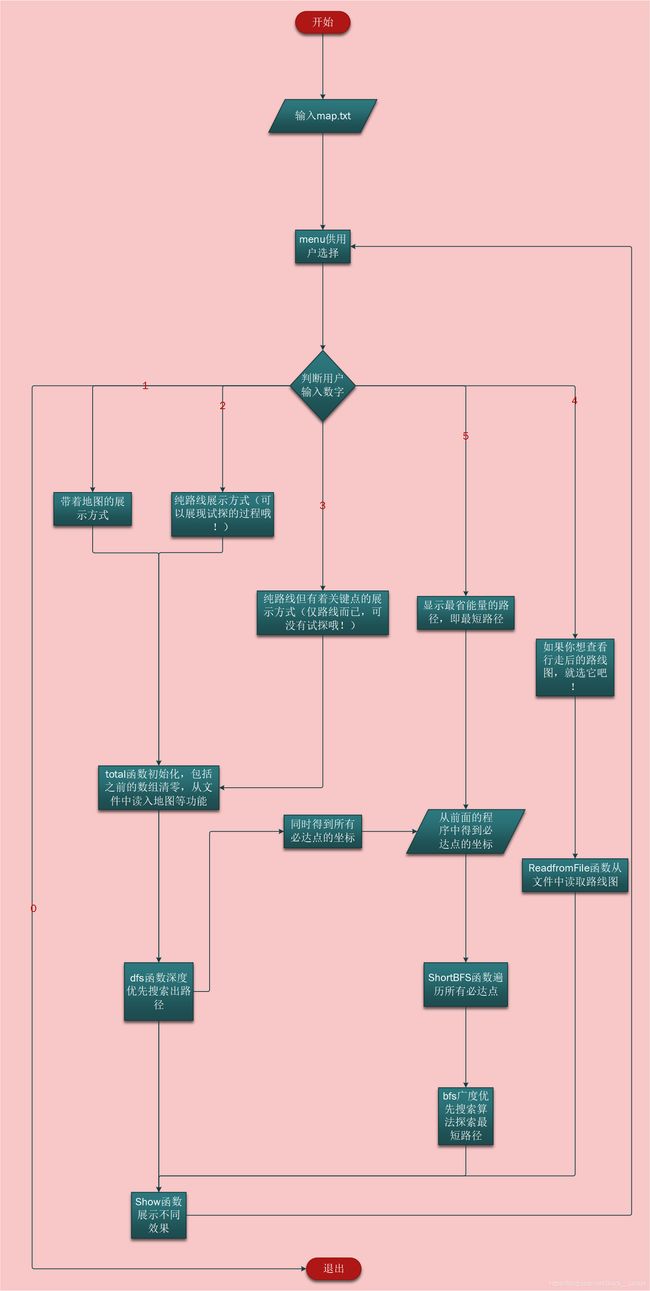
1、带着地图的展示方式
2、纯路线展示方式（可以展现试探的过程哦！）
3、纯路线但有着关键点的展示方式（仅路线而已，可没有试探哦！）
这里着重说明一下，二号方式，是为了充分展现深度优先搜索算法，回溯的特性而专门设置的，用户可以通过这种方式，完整的体验到深度优先搜索算法的实现原理，并希望能对他们以后开发新的功能带来一些启发。

一个简单的小项目而已，希望能够对大家有所帮助！
喜欢的话就点个赞吧！
下面是配套的下载链接，免费的哦！
音乐

地图

代码
下面是测试视频，剪的不太好d=====(￣▽￣*)b凑合着看吧ε=ε=ε=(_￣▽￣)

基于深度优先算法与广度优先算法实现的超高速的机器人未知环境（迷宫）探索

这个是百度云的链接，那个CSDN的我设置的是免费的，但不知道为什么开始收费了，放个百度云链接在这里，方便大家下载d=====(￣▽￣*)b

链接：https://pan.baidu.com/s/1-HgRNiw2a3N7w-63oFwtWg
提取码：zydd

这个是代码、地图文件和音乐文件的放置情况，放在一起就行。另外有很多人问我这个地图文件为什么看不了，因为这个地图我是以二进制的形式进行存储的，所以必须通过程序以二进制的形式进行读取。