Scikit-learn机器学习实战之Kmeans

摘要

上篇博客谈到了如何安装Python中强大的机器学习库 scikit-learn ： Windos环境安装scikit-learn函数库流程 ，本篇主要是对其Kmeans示例进行学习。

有关Kmeans的介绍可以参见这篇博客： K均值聚类算法及Matlab函数使用

Kmeans算法的缺陷

• 聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适
• Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。

（1）第一种缺陷通常人为解决，例如假设有K=10（根据先验知识，尽量大些），进行第一次聚类，如果结果显示某一类中的样本过少，则K=K-1，重新进行聚类。

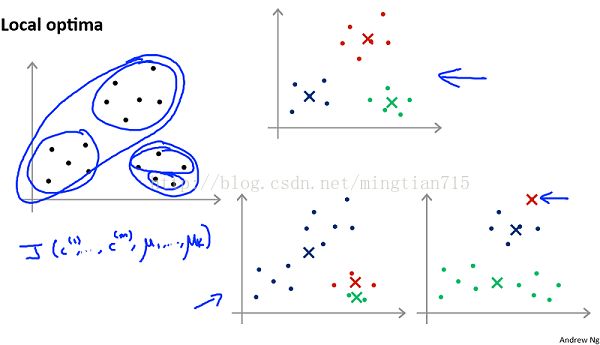
（2）第二种缺陷如下图所示，随机初始化的聚类中心在更新过程中可能陷入局部极小值，造成聚类效果不佳，常用的方法是多次初始化聚类中心，找到使得代价函数最小的初始化中心。

从上图可以看出，如果初始聚类中心间的距离尽可能远的话，聚类的效果可能会更好，因此初始化时应使得聚类中心距离尽可能远（即 Kmeans++ 算法）

Scikit-learn示例

该例为手写识别（数字0~9）数据（8*8图像）的聚类，主要是对Kmeans、kmeans++、以及（Pca+Kmean）做了算法性能比较，并且使用了Pca进行数据可视化。

（1）数据样本

from sklearn.datasets import load_digits
digits = load_digits()
print(digits.data.shape)
(1797, 64)   #1797个数据，每个数据64维
import matplotlib.pyplot as plt 
plt.gray() 
plt.matshow(digits.images[0]) 
plt.show()  

            

（2）算法性能比较

from time import time
import numpy as np
import matplotlib.pyplot as plt

from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale

np.random.seed(42) #随机种子，用于初始化聚类中心

digits = load_digits() #载入数据 
data = scale(digits.data) #中心标准化数据

n_samples, n_features = data.shape #1797，64
n_digits = len(np.unique(digits.target)) #10
labels = digits.target #数据真实标签

sample_size = 300

print("n_digits: %d, \t n_samples %d, \t n_features %d"
      % (n_digits, n_samples, n_features))


print(79 * '_')
print('% 9s' % 'init'
      '    time  inertia    homo   compl  v-meas     ARI AMI  silhouette')

#算法评估函数，包括处理时间、最终代价函数值、以及不同的聚类评价指标
def bench_k_means(estimator, name, data):
    t0 = time()
    estimator.fit(data)
    print('% 9s   %.2fs    %i   %.3f   %.3f   %.3f   %.3f   %.3f    %.3f'
          % (name, (time() - t0), estimator.inertia_,
             metrics.homogeneity_score(labels, estimator.labels_),
             metrics.completeness_score(labels, estimator.labels_),
             metrics.v_measure_score(labels, estimator.labels_),
             metrics.adjusted_rand_score(labels, estimator.labels_),
             metrics.adjusted_mutual_info_score(labels,  estimator.labels_),
             metrics.silhouette_score(data, estimator.labels_,
                                      metric='euclidean',
                                      sample_size=sample_size)))

#Kmeans++，随机初始化10次
bench_k_means(KMeans(init='k-means++', n_clusters=n_digits, n_init=10),
              name="k-means++", data=data)

#Kmeans，随机初始化10次
bench_k_means(KMeans(init='random', n_clusters=n_digits, n_init=10),
              name="random", data=data)

#Pca+kmeans，采用如下调用方式聚类中心是确定的，因此只初始化一次
pca = PCA(n_components=n_digits).fit(data) #fit函数表示拟合数据
bench_k_means(KMeans(init=pca.components_, n_clusters=n_digits, n_init=1),
              name="PCA-based",
              data=data)
print(79 * '_')

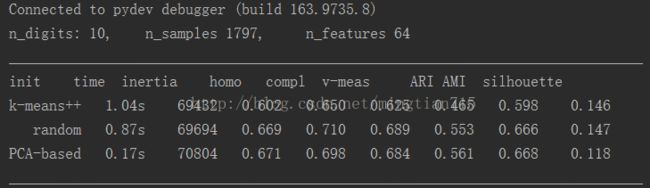
处理结果：

性能上：Kmeans++>random Kmeans>Pca Kmeans，但差别不大。

时间上：Pca Kmeans处理时间远快于另两种算法。并且降维度越低，处理速度越快，但代价函数会逐渐上升，因此寻找一个合适的处理的维度是关键。

PS：这些函数的介绍在 Scikit-learn官网都有介绍；PCA函数也可以参看这篇博客： Scikit-learn中PCA的用法

（3）可视化聚类结果

在（2）中，是将数据从64降维10，再进行Kmeans聚类；在（3）中，为方便可视化，将数据降到2维，进行聚类，可视化。

reduced_data =PCA(n_components=2).fit_transform(data)
#fit_transform得到是用降维度处理后的数据
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data)
#fit表示用括号数据“训练”模型，返回一个kmeans对象

#定义网格步长
# Step size of the mesh. Decrease to increase the quality of the VQ.
h = .02     # point in the mesh [x_min, x_max]x[y_min, y_max].

#定义边界坐标，定义网格坐标
# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

#用训练模型获得网格预测每一点的类值
# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

#绘制函数
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(Z, interpolation='nearest',
           extent=(xx.min(), xx.max(), yy.min(), yy.max()),
           cmap=plt.cm.Paired,
           aspect='auto', origin='lower')

plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
            marker='x', s=169, linewidths=3,
            color='w', zorder=10)
plt.title('K-means clustering on the digits dataset (PCA-reduced data)\n'
          'Centroids are marked with white cross')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())

绘制结果：