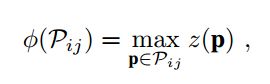ScanContext 论文详解 - 用途：Lidar SLAM 回环检测、空间描述符

Figure 1. 激光雷达沿着方位角(浅蓝)与放射方向（黄）的Bin分割 [1]

Figure 2. Scan Context示意图 [1]

1. 浅读文章

Scan Context，从英文字面理解就是“扫描 上下文”。类比于我们阅读的时候，需要理解上下文，才能明白其意，LidarSLAM在进行回环检测的时候，也需要将“上下文” （之前的数据）进行比较，方才知道我们是不是又走到了之前的同一个地方（回环）。

Scan Context这篇文章由韩国KAIST大学的Giseop Kim和Ayoung Kim所写，它的主要特点是提出了Scan Context这个非直方图的全局描述符，来帮助我们对“上下文”（当前/之前的数据）进行更快速、有效地搜索。典型的应用就是在LiDAR SLAM中进行回环检测和Place Recognition。

2. 提出的方法

• The representation that preserves absolute location information of a point cloud in each bin （如图2所示）
• Efficient bin encoding function
• Two-step search algorithm

3. 算法流程

3.1 Scan Context的创建

(1) 与Shape Context的渊源

Scan Context这个算法其实一开始是由Shape Context [2] 所启发的，而Shape Context是把点云的 local Keypoint 附近的点云形状 encode 进一个图像中。Scan Context的不同在于，它不仅仅是count the number of points,而是采用了maximum height of points in each bin。

(2) 为什么选择Maximum height？

1. The reason for using the height is to efficiently summarize the vertical shape of surrounding structures.
2. In addition, the maximum height says which part of the surrounding structures is visible from the sensor.
3. This egocentric visibility has been a well-known concept in the urban design literature for analyzing an identity of a place

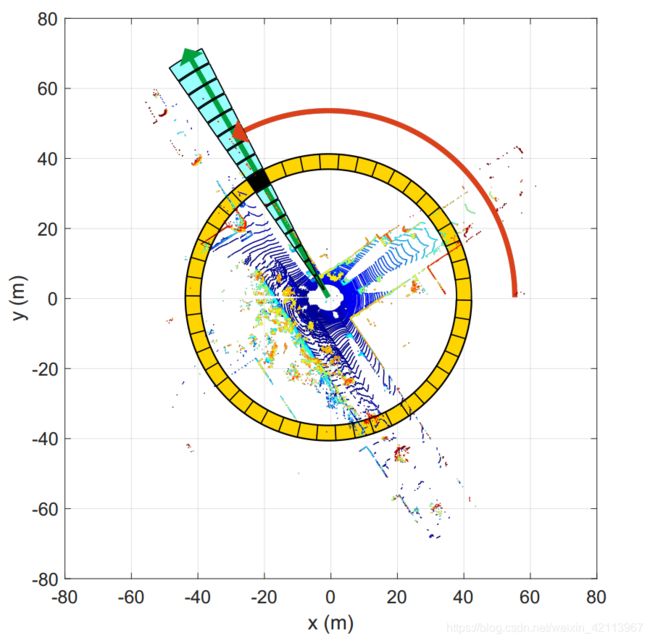
(3) Partition a 3D scan

首先，对每一次Scan进行分割：

• Nr: number of rings （黄色圈圈）
• Ns: number of sectors （浅蓝色/绿色？的格子）
• Lmax: 雷达每一个射线的最远距离
• Radial Gap between rings = $\frac{L_{max}}{N_r}$
• Sector弧度 = $\frac{2\pi }{N_s}$
• 文章中: Nr=20, Ns=60
  

其次，分割后的$P_{ij}$就是指the set of points belonging to the bin where the ith ring and jth sector overlapped。

(4) 给每个Bin进行赋值：Bin Encoding

• $z(\cdot )$ 是指point P 的Z坐标。
• 直接使用最大z坐标值 $z(p)$，作为这个bin的value。

(5) Scan Context Matrix

A scan context I is finally represented as a Nr × Ns matrix as:

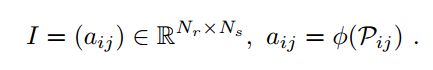
3.2 Similarity Score的计算

假设我们得到了一对Scan Context的矩阵，我们要计算他们俩($I_p,I_c$)之间的相似度，文章中采用了columnwise (按列) 的距离计算。

• $I_q$: Query Point Cloud (简言之，我们当前用来query的点云)
• $I_c$: Candidate Point Cloud （咱们的“数据库”中储存的用来匹配的candidate点云）
• $c_j^q$: Column j of Query Point Cloud （列向量）
• $c_j^c$: Column j of Candidate Point Cloud （列向量）
  

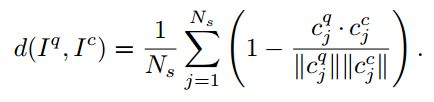
小红薯：且慢，大师兄！
小红薯：古希腊哲学家赫拉克利特说，“人不能两次踏进同一条河流”。
小红薯：这样来比较两个点云，而没考虑每次不可能在exactly同一个位置和角度观察，是不是too young, too simple了呢！
–
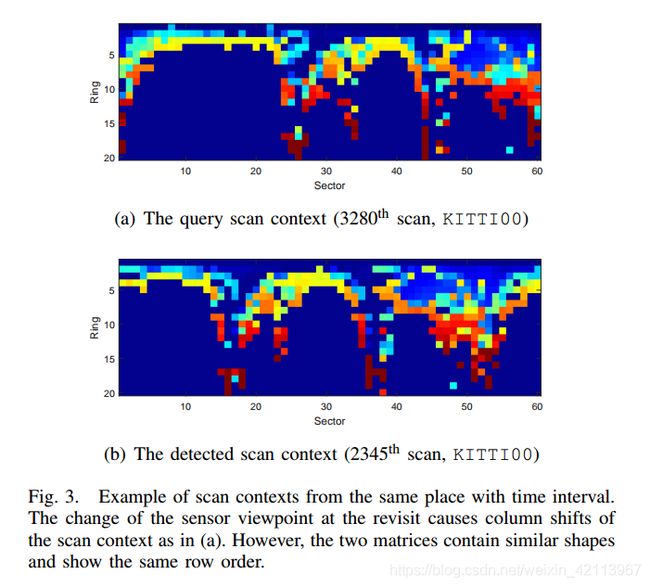
大师兄：恩，这是个好问题。假设咱们回到同一个地方，那有可能是沿着相反的方向回来的，那咱们的Viewpoint就发生了变化，这个Scan Context矩阵就会发生偏移！这样就会导致Column顺序发生变化。
大师兄：所幸的是，只要location是在同一个地方，不管你的方向朝着哪里，至少row order不会发生太大变化。咱们只需要关心column shift这个问题。

在文章中，上面大师兄和小红薯对话中的问题，如下图所示：

Figure 3. Column Shift示意图 [1]

咱们可以看到在column方向发生了水平位移，但是竖着的row方向没有变化。

为了解决这个问题，文中采用了一个“地球人都能想到的方法”，那就是不断尝试各种角度的column shift。注意的是，旋转candidate point cloud有个resolution，那就是之前提到的$\frac{2\pi }{N_s}$。
我们使用公式(7)进行最佳shift的选择，找到最好的$n^{\ast }$后，用公式(6)进行distance计算。

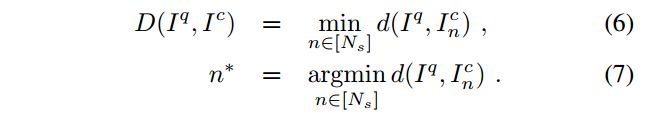
注意：这里咱们通过找最好的$n^{\ast }$，还有一个意想不到的好处，那就是可以给ICP提供一个Good initial rotation value! (就是ICP代码中的predicted pose)

3.3 Two-phase Search Algorithm

文中提到，有三种主流的Place Recognition的Search Algorithm:

• Pairwise Similarity Scoring
• Nearest Neighbor Search搜索
• Sparse Optimization

本文中采用了pairwise scoring和nearest search来实现有效的Hierarchical Search。

(1) Ring Key

在3.2节中我们提到的公式(6)进行最短距离计算时，要先找到最佳旋转$n^{\ast }$，计算量很大，所以在本文中提出了一种"Two-phase Search"，并提出了Ring key这个Descriptor（描述子）来进行匹配搜索：

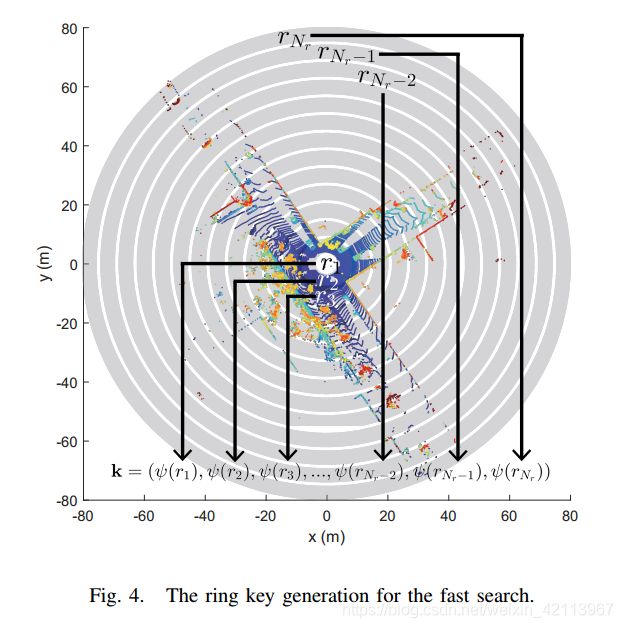
Ring key is a rotation-invariant descriptor, which is extracted from a scan context. Each row of a scan context, r, is encoded into a single real value via ring encoding function . The first element of the vector k is from the nearest circle from a sensor, and following elements are from the next rings in order as illustrated in Fig. 4

Figure 4. Ring key示意图 [1]

由内而外，一圈一圈的ring key通过对Scan Context Matrix的每一行row $r$进行$\psi (\cdot )$的encoding就变成了一个$N_r$维度的Vector $\text{k}$:

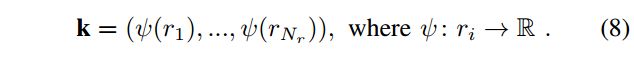
The ring encoding function $\psi$ is a occupancy ratio using $L_0$ norm:

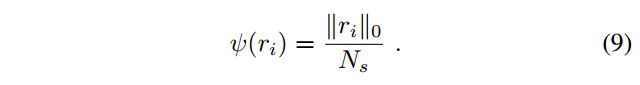
小红薯：大师兄，这里的$||r_i|{|}_0$是什么意思呢？
大师兄：这是$L_0$ norm（范数）的意思，其实$L_0$ norm并不是一个真正的norm，它就是the total number of non-zero elements in a vector 。比如,(2,0,1,0,9)这个vector的$L_0$ norm就是3，因为有3个非零数。
大师兄： 这样一来，咱们统计每一圈的row中有多少个非零数值，那这就和rotation没啥关系啦（也就是原文中所说的rotation invariance）！这样就能够达到快速的search。

(2) KD-Tree

• 在得到ring key向量 $\text{k}$ 之后，文章用了$\text{k}$构建KD Tree。
• 用ring key of the query到这个KD Tree中搜索K个最相似的scan indexex（K是个heuristic number）
• 得到最相似的K个scan后，用上文中公式(6)进行Similarity Score计算
• 满足条件的最近的candidate $c^{\ast }$这个位置被选为revisited place，也就是loop的地方:
  

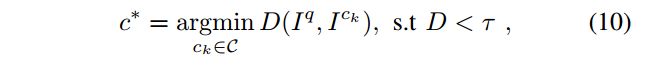
4. Scan Context算法延伸

4.1 ICP Initial Value中的应用

由上文3.2节的公式（7）需要找到一个$n^{\ast }$旋转，使得两个点云之间的距离最小。这里其实也可以作为ICP的一个初始值，即predicted pose，来加快converge的过程。

文章的Experiment部分对此进行了试验，发现用Scan Context进行ICP初始化效果确实更好：

Figure 5. SC在ICP初始化中的应用 [1]

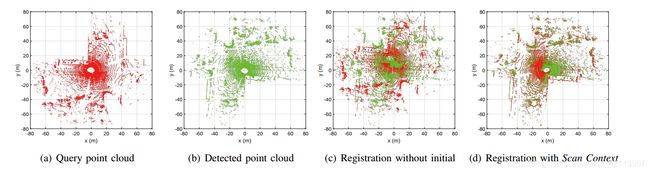
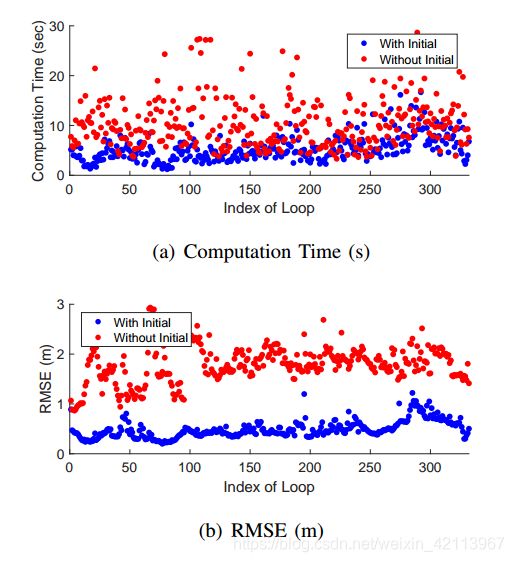
4.2 Future Works

在文章最后，作者提到可以使用更好的bin encoding function (eg., a bin’s segmantic information)来提升性能，目前咱们只是用了一个很简单的$maxZ(p)$来找Z轴高度上的最高点。

对于有梦想的读者，也期待你的贡献！

---

参考文献

[1] G. Kim and A. Kim, “Scan Context: Egocentric Spatial Descriptor for Place Recognition Within 3D Point Cloud Map,” 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, 2018, pp. 4802-4809, doi: 10.1109/IROS.2018.8593953.

[2] S. Belongie, J. Malik, and J. Puzicha, “Shape matching and object recognition using shape contexts,” IEEE Trans. Pattern Analysis and Machine Intell., vol. 24, no. 4, pp. 509–522, 2002.