寒假CS每日打卡 Feb.15th

---

算法部分

1.Acwing 入门组每日一题
题目：拼写正确
给定一个非负整数 N，你的任务是计算 N 的所有数字的总和，并以英语输出总和的每个数字。

输入格式
共一行，包含一个整数 N。

输出格式
共一行，用英语输出总和的每个数字，单词之间用空格隔开。

数据范围
0≤N≤10100
输入样例：
12345
输出样例：
one five

题解：
  简单的字符串题目。

代码：

#include 
#include 
#include 

using namespace std;

string fun(int a){
     
    string s;
    
    while(a){
     
        s.push_back(a % 10 + '0');
        a /= 10;
    }
    reverse(s.begin(), s.end());
    if(s.empty())
        s.push_back('0');
    return s;
}

int main(){
     
    string arr[10] = {
     "zero", "one", "two", "three", "four", "five", "six", "seven", "eight", "nine"};
    string s;
    int sum = 0;
    
    cin >> s;
    for(char c : s)
        sum += c - '0';
    
    s = fun(sum);
    for(char c : s)
        cout << arr[c - '0'] << " ";
    return 0;
}

2.Acwing 提高组每日一题
题目：机器人跳跃问题
机器人正在玩一个古老的基于DOS的游戏。
游戏中有N+1座建筑——从0到N编号，从左到右排列。
编号为0的建筑高度为0个单位，编号为 i 的建筑高度为H(i)个单位。
起初，机器人在编号为0的建筑处。
每一步，它跳到下一个（右边）建筑。
假设机器人在第k个建筑，且它现在的能量值是E，下一步它将跳到第k+1个建筑。
如果H(k+1)>E，那么机器人就失去H(k+1)-E的能量值，否则它将得到E-H(k+1)的能量值。
游戏目标是到达第N个建筑，在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏，才可以保证成功完成游戏？

输入格式
第一行输入整数N。
第二行是N个空格分隔的整数，H(1),H(2),…,H(N)代表建筑物的高度。

输出格式
输出一个整数，表示所需的最少单位的初始能量值上取整后的结果。

数据范围
1≤N,H(i)≤105,

输入样例1：
5
3 4 3 2 4
输出样例1：
4
输入样例2：
3
4 4 4
输出样例2：
4
输入样例3：
3
1 6 4
输出样例3：
3

题解：
  利用二分法来暴力求解，当某一刻能量大于100000后肯定能跳到最后，此时应当跳出循环，因为高度最大值也就为100000。

代码：

#include 

using namespace std;

const int MAXN = 1e5 + 10;
int arr[MAXN], n;

bool check(int mid){
     
    for(int i = 0; i < n; i ++){
     
        mid += mid - arr[i];
        if(mid < 0)
            return false;
        if(mid > MAXN)
            return true;
    }
    return true;
}

int main(){
     
    cin >> n;
    for(int i = 0; i < n; i ++)
        cin >> arr[i];
    
    int le = 1, ri = MAXN, mid;
    while(le < ri){
     
        mid = le + ri >> 1;
        //合法就缩小初始能量
        if(check(mid))
            ri = mid;
        else
            le = mid + 1;
    }
    cout << ri << endl;
    return 0;
}

3.LeetCode 每日一题
题目：最大连续1的个数
给定一个二进制数组， 计算其中最大连续1的个数。

示例 1:
输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.

注意：
输入的数组只包含 0 和1。
输入数组的长度是正整数，且不超过 10,000。

题解：
  利用双指针线性求解。

代码：

class Solution {
     
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
     
        int pre = 0, ans = 0;

        for(int i = 0; i < nums.size(); i ++){
     
        	//为 0
            if(!nums[i]){
     
            	//更新答案
                ans = max(ans, i - pre);
                //找到下一个1的位置
                while(i < nums.size() && !nums[i])
                    ++ i;
                //更新pre
                pre = i;
            }
        }
        ans = max(ans, (int)nums.size() - pre);
        return ans;
    }
};

4.力扣228周赛 – 一个图中连通三元组的最小度数
题目：
给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。
一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。
连通三元组的度数 是所有满足此条件的边的数目：一个顶点在三元组内，而另一个顶点不在三元组内。
请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

示例 1：

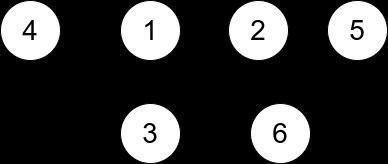
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

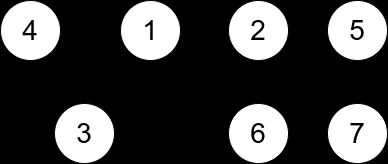
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：

1. [1,4,3]，度数为 0 。
2. [2,5,6]，度数为 2 。
3. [5,6,7]，度数为 2 。

提示：
2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= ui, vi <= n
ui != vi
图中没有重复的边。

题解：
  三层for循环遍历所有的三元组来求解，纯暴力，注意到提示中说到图没有重复的边，可以将两个数字哈希到一个数字，以此来判断两点之间的边是否存在。

代码：

bool cnt[200010];

class Solution {
     
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
     
        int ans = INT_MAX;
        memset(cnt, 0, sizeof(cnt));
        vector<int> degree(n + 1, 0);

        for(auto &i : edges){
     
        	//保证边的first一定大于second
            if(i[0] > i[1])
                swap(i[0], i[1]);
            //哈希到一维，n最大为400，500已经能保证没有冲突
            cnt[i[0] * 500 + i[1]] = true;
            //两条边的入读 + 1
            degree[i[0]] ++;
            degree[i[1]] ++;
        }
		//3层for循环遍历所有的三元组
        for(int i = 1; i <= n; i ++){
     
            for(int j = i + 1; j <= n; j ++){
     
                if(!cnt[i * 500 + j])
                    continue;
                for(int k = j + 1; k <= n; k ++){
     
                    if(cnt[i * 500 + k] && cnt[j * 500 + k])
                    	//-6 因为三元组内部有6个度
                        ans = min(ans, degree[i] + degree[j] + degree[k] - 6);
                }
            }
        }
        return ans == INT_MAX ? -1 : ans;
    }
};

---

书籍部分

算法竞赛.进阶指南 0x61最小生成树 ✔
LeetBook 硬核操作系统指南 计算机硬件介绍 ✔
LeetBook 硬核 Linux 攻略 Linux简介 ✔

---

PS.