机器学习算法的总结介绍一（超全面）：线性回归；逻辑回归；支持向量机；集成学习；朴素贝叶斯；KNN

---

前言

本文介绍了机器学习算法中经典的有监督算法（线性回归，逻辑回归，支持向量机，集成学习（随机森林&AdsBoot），朴素贝叶斯和KNN），不包括无监督算法和深度学习算法。

---

一、线性回归（Linear regression）

线性回归都是通过把一系列数据点预测计算出一条合适的“线”，将新的数据点映射到这条预测的“线”上，继而做出预测。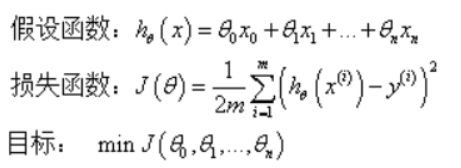

如图，线性回归预测的是直线，这就意味着线性回归的表达式是线性的。
线性回归的损失函数（loss）一般是最小均方误差（MSE）。loss函数的优化方式一般是最小二乘法或者梯度下降法。

岭回归和Lasso回归（即，加入正则项的线性回归）

使用多项式回归，如果多项式最高次项比较大，模型就容易出现过拟合。正则化是一种常见的防止过拟合的方法，一般原理是在代价函数后面加上一个对参数的约束项，在保证最佳拟合误差的同时，使得参数尽可能的“简单”，使得模型的泛化能力强（即不过分相信从训练数据中学到的知识）。这个约束项被叫做正则化项（regularizer）。在线性回归模型中，通常有两种不同的正则化项：

加上所有参数（不包括θ0）的绝对值之和，即l1范数，此时叫做Lasso回归；
加上所有参数（不包括θ0）的平方和，即l2范数的平方，此时叫做岭回归.

损失函数如图：

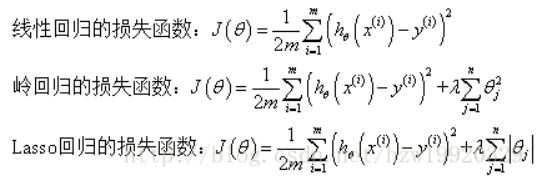
其中λ称为正则化参数，如果λ选取过大，会把所有参数θ均最小化，造成欠拟合，如果λ选取过小，会导致对过拟合问题解决不当，因此λ的选取是一个超参数。

岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项，Lasso回归引入的是L1范数惩罚项，Lasso回归能够使得损失函数中的许多θ均变成0，这点要优于岭回归，因为岭回归是要所有的θ均存在的，这样计算量Lasso回归将远远小于岭回归。

从贝叶斯角度看，lasso（L1 正则）等价于参数 ww 的先验概率分布满足拉普拉斯分布，而 ridge（L2 正则）等价于参数 ww 的先验概率分布满足高斯分布。

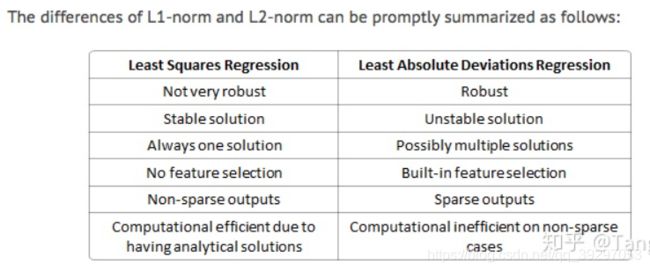
L1 正则化会比 L2 正则化让线性回归的权重更加稀疏，即使得线性回归中很多权重为 0，而不是接近 0。或者说， L1 正则化（lasso）可以进行 feature selection，而 L2 正则化（ridge）不行。

二、逻辑回归（Logistic regression）

基础公式
f(x) = wx + b
y = sigmoid(f(x))
可以看作是一次线性拟合+一次sigmoid的非线性变化

逻辑回归的损失函数（loss）一般为cross entropy，而且而逻辑回归加入sigmoid函数后，函数复杂不易直接用最小二乘求解所以采用梯度下降算法优化loss函数。

虽然逻辑回归能够用于分类，不过其本质还是线性回归。它仅在线性回归的基础上，在特征到结果的映射中加入了一层sigmoid函数（非线性）映射，即先把特征线性求和，然后使用sigmoid函数来预测。

满足什么样条件的数据用LR最好？
特征之间尽可能独立

离散特征，连续特征通常没有特别含义，31岁和32岁差在哪？

使的lr在某种确定分类上的特征分布满足高斯分布

最后，一般来说，线性回归主要用来做预测，逻辑回归主要用来做分类。

---

三，支持向量机（SVM）

SVM最初被提出是用来解决二分类问题，又名最大间距分类器，目的是在众多符合条件的结果中挑选最好的结果（该结果距离不同的样本点的区域都最大），这时的结果鲁棒性最好。

对于用于分类的支持向量机来说，给定一个包含正例和反例（正样本点和负样本点）的样本集合，支持向量机的目的是寻找一个超平面来对样本进行分割，把样本中的正例和反例用超平面分开，但是不是简单地分看，其原则是使正例和反例之间的间隔最大。

超平面是什么呢？简单地说，超平面就是平面中的直线在高维空间中的推广。那么，对于三维空间，超平面就是平面了。对于更高维的空间，我们只能用公式来表达，而缺少直观的图形了。总之，在n维空间中的超平面是n-1维的。

SVM有三宝：间隔，对偶，核技巧

SVM分类：
硬SVM分类器（线性可分）：当训练数据可分时，通过间隔最大化，直接得到线性表分类器
软SVM分类器（线性可分）：当训练数据近似可分时，通过软间隔最大化，得到线性表分类器
kernel SVM：当训练数据线性不可分时，通过核函数+软间隔的技巧，得到一个非线性的分类器

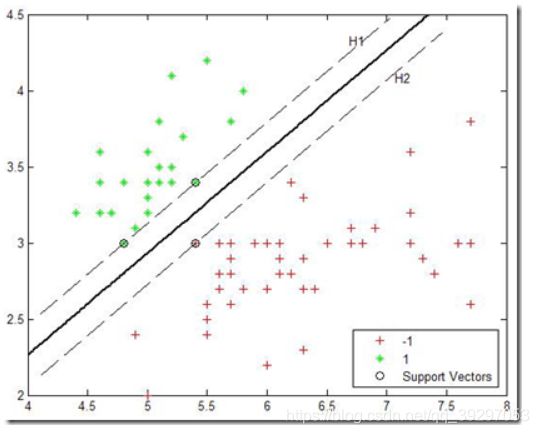
如图所示，是一个二分类问题的硬间隔SVM的函数表示。
为了更形象地表现正负样本的间隔，我们可以在分割超平面的两侧再定义两个超平面H1和H2（如图中虚线所示），这两个超平面分别通过正样本和负样本中离分割超平面最近的样本点（图中加了外圈）。从以上分析可以知道，超平面H1和H2离分割超平面是等距的。

我们定义超平面H1和H2上面的点叫做支持向量。正负样本的间隔可以定义为超平面H1和H2之间的间隔，它是分割超平面距最近正样本点距离和最近负样本点距离之和。

从图中可以看出，支持向量对于分割超平面的位置是起到关键作用的。在优化分割超平面位置之后，支持向量也显露出来，而支持向量之后的样本点则对分类并不关键。为什么这样说呢？因为即使把支持向量以外的样本点全部删除，再找到最优的分割超平面，这个超平面的位置跟原先的分割超平面的位置也是一样的。总结起来就是：

支持向量包含着重构分割超平面所需要的全部信息！

软间隔SVM是指允许样本点有少量的混淆。
当样本点混淆严重到线性不可分的时候，就需要通过核函数将样本点映射到更高维的空间，高到什么程度呢？直到样本点在该高维空间每个平面都线性可分。通过这个核函数对样本进行先升维后分类的方法是核SVM（kernel SVM）

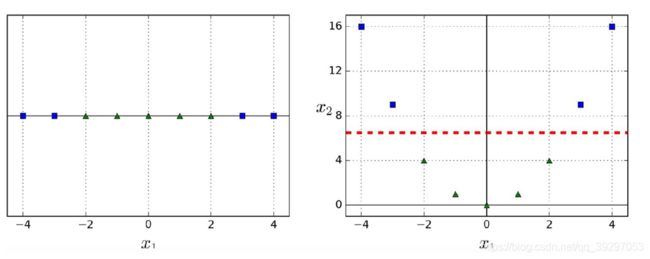
如图所示，当这个二分类问题在图一这个一维的空间线性不可分时，将这两类样本通过核函数映射到二维空间之后，就变成了线性可分问题。
常用的核函数有：
线性核函数：主要用于线性可分的情形。参数少，速度快。
多项式核函数：
高斯核函数：主要用于线性不可分的情形。参数多，分类结果非常依赖于参数。
sigmoid 核函数：
拉普拉斯核函数：
用的比较多的是线性核函数和高斯核函数，线性用于特征多，线性问题的时候，高斯核函数用于特征少，非线性问题需要升维的时候。最好SVM采用的是hingeloss作为损失函数。

对于对偶问题的解释含有的数学概念比较复杂，这里不做解释，对偶的方式和好处如图所示：

四，集成学习（Ensemble Learning）

集成学习的核心思想是综合多个简单的分类器做出共同决断。相当于群体决策，用拟人的方法解释就是一个班级相当于一个集成学习模型，每个学生相当于一个分类器，单个学生（一个分类器）做出的决策肯定没有整个班级所有学生（所以学生）讨论做出的决策更有价值。

如果一个班级全是男孩，那么我们说这个集成学习模型的基学习器是同质的；如果一个班级有男孩有女孩，我们说这个模型的基学习器是异质的。

另外，如果全班同学同时回答问题，我们说这个模型的结果是并行（bagging）生成的，不存在强依赖关系，类似的模型有随机森林；全班同学依次回答问题，我们说这个模型的结果是串行（boosting）生成的，存在强依赖关系，类似的模型有提升树。bagging，关注于提升分类器的泛化能力；boosting，关注于提升分类器的精度。

另外，值得注意的是：一个复杂的模型容易产生较大的方差和出现过拟合现象，Bagging方式可以减缓这种现象，因为它将复杂的模型分成了多个简单的模型。
对于Boosting来说，如果设计的机器学习算法产生的分类错误率小于50%，理论上上可以通过Boosting将错误率降低到无限接近于0.

随机森林（Random forest）

随机森林=bagging+决策树

随机：特征选择随机+数据采样随机
特征随机是在决策树每个结点上选择的时候随机，并不是在每棵树创建的时候随机。
每个结点上对特征选择都是从全量特征中进行采样对，不会剔除已利用的。

数据采样，是有放回的采样
1个样本未被选到的概率为p = (1 - 1/N)^N = 1/e，即为OOB

森林：多决策树组合
可分类可回归，回归是对输出值进行简单平均，分类是对输出值进行简单投票

决策树
如图所示，描述了一个通过决策树解决的简单二分类问题。

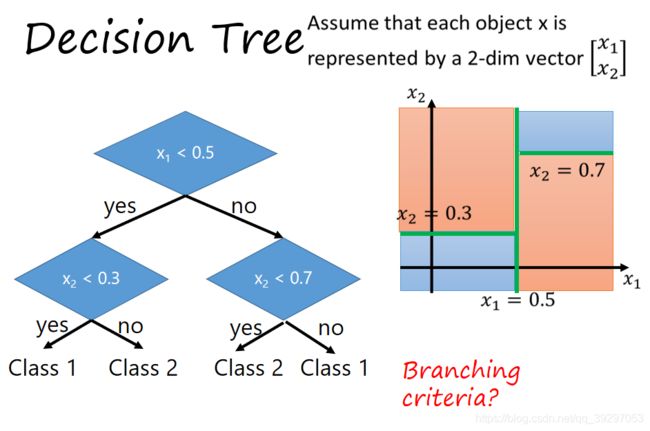
常见的决策树的基本结构如下：

简单是解释一下什么是cart树：
CART，又名分类回归树，是在ID3的基础上进行优化的决策树，学习CART记住以下几个关键点：

（1）CART既能是分类树，又能是分类树；

（2）当CART是分类树时，采用GINI值作为节点分裂的依据；当CART是回归树时，采用样本的最小方差作为节点分裂的依据；

（3）CART是一棵二叉树。

提升树（Boosting tree）

提升树=bagging+AdsBoost决策树

Adaboost算法是一种提升方法，将多个弱分类器，组合成强分类器。
AdaBoost，是英文”Adaptive Boosting“（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。
它的自适应在于：前一个弱分类器分错的样本的权值（样本对应的权值）会得到加强，权值更新后的样本再次被用来训练下一个新的弱分类器。在每轮训练中，用总体（样本总体）训练新的弱分类器，产生新的样本权值、该弱分类器的话语权，一直迭代直到达到预定的错误率或达到指定的最大迭代次数。

算法原理
（1）初始化训练数据（每个样本）的权值分布：如果有N个样本，则每一个训练的样本点最开始时都被赋予相同的权重。
（2）训练弱分类器。具体训练过程中，如果某个样本已经被准确地分类，那么在构造下一个训练集中，它的权重就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。同时，得到弱分类器对应的话语权。然后，更新权值后的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。
（3）将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，分类误差率小的弱分类器的话语权较大，其在最终的分类函数中起着较大的决定作用，而分类误差率大的弱分类器的话语权较小，其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的比例较大，反之较小。

五，朴素贝叶斯分类(Naive Bayesian classification)

对于给出的待分类项，求解此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类属于哪个类别。贝叶斯公式为：p(A|B)= p(B|A)*p(A/p(B)，其中P(A|B)表示后验概率，P(B|A)是似然值，P(A)是类别的先验概率，P(B)代表预测器的先验概率。

优点：在数据较少的情况下仍然有效，可以处理多类别问题。

缺点：对输入数据的准备方式较为敏感。

应用场景：文本分类、人脸识别、欺诈检测。

六，k-近邻算法(K-Nearest Neighbor，KNN)

KNN是一种基于实例的学习，采用测量不同特征值之间的距离方法进行分类。其基本思路是：给定一个训练样本集，然后输入没有标签的新数据，将新数据的每个特征与样本集中数据对应的特征进行比较，找到最邻近的k个(通常是不大于20的整数)实例，这k个实例的多数属于某个类，就把该输入实例分类到这个类中。

优点：简单、易于理解、易于实现，无需估计参数。此外，与朴素贝叶斯之类的算法比，无数据输入假定、准确度高、对异常数据值不敏感。

缺点：对于训练数据依赖程度比较大，并且缺少训练阶段，无法应对多样本。

应用场景：字符识别、文本分类、图像识别等领域。