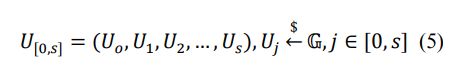Anonymous scheme for blockchain atomic swap based on zero-knowledge proof

Anonymous scheme for blockchain atomic swap based on zero-knowledge proof

---

摘要

区块链的跨链原子交换可以通过使用智能合约来代替可信的第三方，但是原子交换不能保证交易的匿名性和隐私性，因此，这篇论文提出一种基于零知识证明的原子交换。

---

Hash Lock

Assuming a real trading scenario, Alice holds 1 BTC and Bob holds 100 ETH.

Alice wants to use her 1 BTC to exchange the 100 ETH in Bob’s account.

Previously they usually chose a large exchange as a third party for trading, and put your own money on the exchange to exchange assets. This method is possible,but there are corresponding risks.

Finally, they decided to use atomic exchange to exchange.Alice first sent her 1BTC to a smart contract. The BTC is saved. When the smart contract receives B’s public key and a random number x, the smart contract will send Alice’s BTC to Bob. At the same time, there is a time limit on the smart contract. If you do not receive the unlocking information within this time, BTC will be returned to Alice. This time limit is called hash time lock.
. . .
看图可以解释整个过程的。

---

However

Traditional atomic swap technology uses smart contracts on two chains to set up transactions, but the information on the smart contract is open and transparent.

Enter the address of the smart contract in the browser, and you can clearly see all the code information in the smart contract.

Therefore, the traditional atomic exchange is information secure but does not have anonymity.

---

In the blockchain, the hash value of each transaction is stored in the
form of a Merkel Tree.

set the storage of the hash value to two lists

• a full hash list

  • contains the hash values of all transactions in the chain

• an nullifier list

  • contains the hash values of transactions that have already been performed.

---

the original input-output structure of the transaction --> a Note structure
the hash value of the Note structure --> H

---

left side --> the hash value of all transactions
right side --> the transaction that has been spent.

---

The specific scheme

1.Alice
- finds one or more unspent notes
- Use zeroknowledge proof to prove that you own the asset of ܰNote₁

Initial stage

use libsnark to implement zkSNARKs.

generate a common reference string, or a pair of ݁݇ek and vk.

• When performing trusted settings, select some random numbers to calculate ݁݇ek and vk,݇but these random numbers cannot be known by the prover and verifier.
• The trusted setting should be done by a trusted third party

ek is used to generate the ܵproof, and vk ݇is used to verify the ܴ proof.

We use the symbol ݉m_{[1,q][1,n][0,s]} to represent the asset of ܰNote₁,and the initialization program randomly generates s+1 group elements:

ps:疑问为什么会是m_{[1,q][1,n][0,s]}？
： 这里是一个矩阵输入！！！用于表达note数据结构

---

The initializer calculates (n, q) validators:

O_[1,q][1,n]

	- a common input
	- shared between the sender and the receiver

---

Another job of the initialization program is to set zkSNARK with the circuit C ,which calculates the hash value:

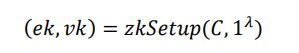
ek ݁݇ is the evaluation key of the sender, and vk ݇is the authentication key of the receiver.

---

Rܴ first uses the key bound to the key promise to verify that the authenticated encrypted data is correct:

---

Then the knowledge of the R verification key proves -

---

2.After Alice proves her ownership of the transaction Note₁

• decrypts ܰNote₁ with her private key sk
• obtains the data in ܰNote₁
• creates two new ܰNote₂ and Note₃

Note₂: set to send to the smart contract
Note₃: send the balance in Note₁ to your account address.

3.Alice:

• sends the hash value H₁ of Note₁ to the node network of the blockchain.
• the node will determine whether the hash value exists in the discard list.
  • exists: double spent
  • Otherwise: recorded in the discard list
• sends the hash values of Note₂ and ܰ Note₃ to the node

The transaction sent by Alice to the smart contract is hidden,and the address of the smart contract cannot be found .

ps:因为这里只能追溯到Note₁的序号索引以及H值，从而在将资产存储到智能合约的过程中实现匿名。

---

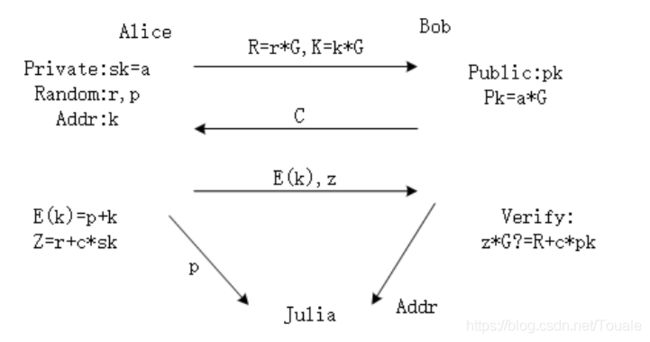
Original exchange contract address

---

Improved protocol exchange

---

Alice’s private key --> sk
Bob owns the public key -->pk

---

New problem

Bob needs to verify that the private key owned by Alice is the correct private key corresponding to the public key, and that Alice and Bob can exchange the contract address of the assets stored by both parties through the smart contract

solve：

---

---

Zero-knowledge proof

感觉很清晰的一个例子，，，

接着只要证明 P₁ + P₂= Q，重复步骤循环m次，证明Gen知道s值，且奇妙之处在于证明拥有s值但不需要传递s值

---

总结

本文讲述了一个基于零知识证明的原子交换跨链，相比于原来仅仅基于智能合约的哈希锁定，在隐私性，匿名性起到了很好的保护效果，本文中涉及公式较多，且过程相比最初的哈希锁定还是比较复杂，目前来看，还是存在一知半解，仅以博客，日后回溯能从中get到一些新的idea。