Pytorch学习笔记-LSTM
目录
-
- 1. LSTM原理
-
- 1.1 Recurrent Neural Network
- 1.2 LSTM Network
- 1.3 The Core Idea Behind LSTMs
- 1.4 三个门控开关
-
- 1.4.1 LSTM:Forget gate
- 1.4.2 LSTM:Input gate and Cell state
- 1.4.3 LSTM:Output gate
- 1.5 LSTM如何解决梯度消失
- 2. LSTM Layer使用
-
- 2.1 nn.LSTM
- 2.1 nn.LSTMCell
- 3. 感情分类实战
- 4. Reference
1. LSTM原理
1.1 Recurrent Neural Network
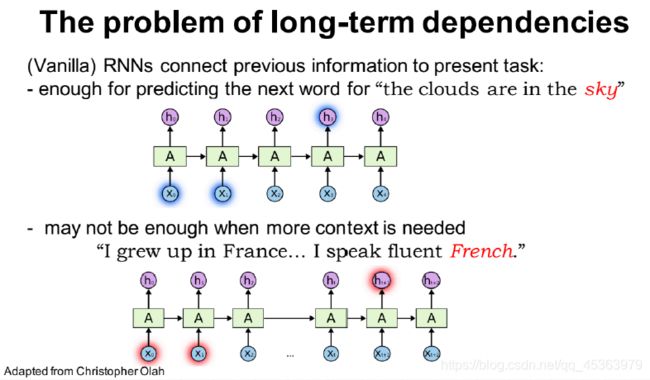
经过上一篇文章推导,RNNs最有价值得地方在于它可以将先前的信息与当前的任务联系起来,比如使用先前的视频帧可以帮助理解当前帧。如果RNNs能做到这一点,它们将非常有用。但他们能吗?视情况而定。
从这张图片可以看出,当句子较短,只需要最近得信息就可以执行当前任务,比如第一句话,试图“云在__中”,我们不需要大量的上下文信息,就可以预测出“云在天空中”。但是现实生活中往往像第二句话一样,就需要更多的上下文信息,“我在法国长大,法语说得很流利“。可以看出,预测的是一门语言,但是想要缩小范围,就只能更久远的法国,才能预测出这是法语。这就可以看出随人RNNs在计算中包含了全文,但是实际操作中,他的memory只能记住周围几个。
从理论上讲,RNNs绝对能够处理这种“长期依赖关系”。可以通过调节参数来解决现有的问题。但是在实践中RNNs无法学会他们。Hochreiter (1991) [German]和Bengio等人(1994)对这个问题进行了深入的探索,他们发现了一些非常基本的原因,为什么它可能很难。
- RNN存在的问题:
1.梯度消失
2.梯度爆炸
3.只能进行短期记忆
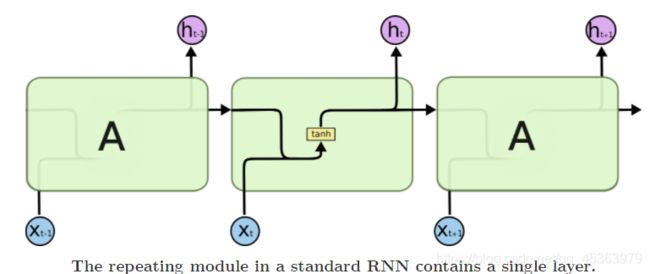
所有的RNN都可以表示成神经网络模块重复链的形式。在标准的RNNs中,这个重复模块将有一个非常简单的结构,比如一个单一的tanh层。
1.2 LSTM Network
LSTM同样拥上述的链式结构,只是重复块中的结构与RNN不同,不是只有一个神经网络层,而是有四个,以一种非常特殊的方式相互作用。
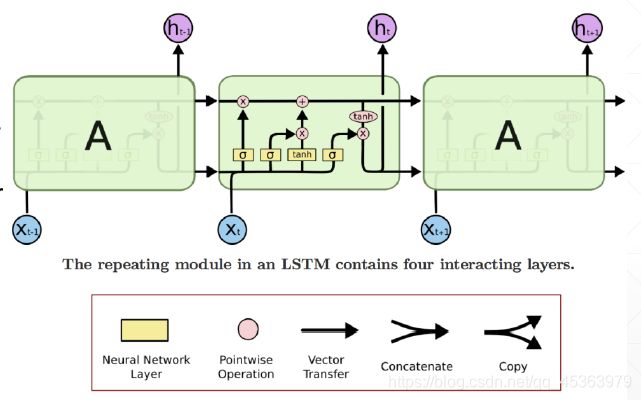
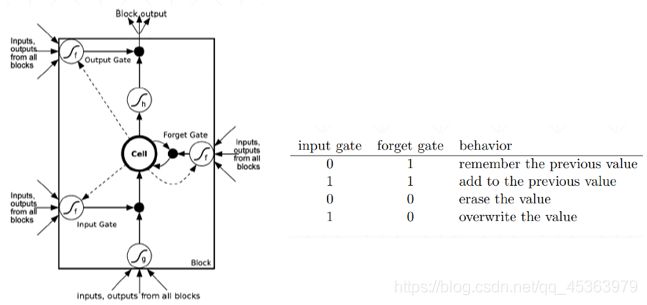
设置了三个 σ \sigma σ门控开关, σ \sigma σ(sigmod)层可以生成0-1的数。通俗点说 σ \sigma σ相当于一个闸门。对于 h t − 1 h_{t-1} ht−1经过一个闸门,来控制对于上一时刻的memory保留到这一时刻的多少,当 σ \sigma σ=1时对于之前的memory全部保留,当 σ \sigma σ=0则对之前的memory全部抛弃。然后对于当前时刻的输入 x t x_t xt也是同理,之后在将当前时刻与之前 h t h_t ht进行融合之后在经过一个门控开关,来控制到下一时刻的输出量。
1.3 The Core Idea Behind LSTMs
LSTMs的关键是cell state,即贯穿图表顶部的水平线。
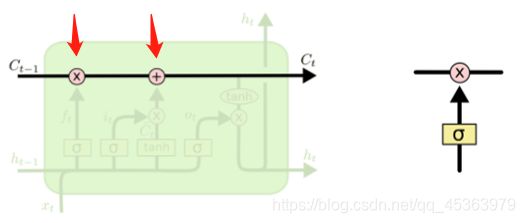
LSTM确实有能力删除或添加信息到cell state,由称为门的结构仔细地调节。
门是一种选择性地让信息通过的方式。它们由一个s型神经网络层和一个点态乘法运算组成。
下面我们开始分别介绍三个门的作用
sigmoid层输出0到1之间的数字,描述每个组件有多少应该被允许通过。值为零意味着“不让任何东西通过”,值为1意味着“让所有东西通过”。
即相乘代表信息过滤,相加代表信息融合。
1.4 三个门控开关
1.4.1 LSTM:Forget gate
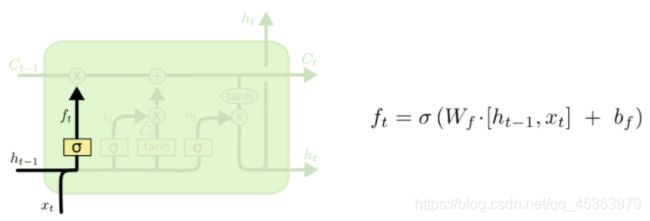
第一个门成为遗忘门,通过 σ \sigma σ实现,决定cell state中那些信息应该被抛弃。
它根据 h t − 1 h_{t−1} ht−1和 x t x_t xt,并为cell state C t − 1 C_{t−1} Ct−1中的每个数字输出0和1之间的数字。1表示“完全保留这个”,而0表示“完全删除这个”,即 C t − 1 C_{t−1} Ct−1完成了信息过滤。
让我们回到语言模型的示例,该语言模型试图根据前面的所有单词预测下一个单词。在这样的问题中,cell state可能包括现在主语的性别,这样就可以使用正确的代词。当我们看到一个新主语时,我们想忘记旧主语的性别。
值得注意的是,每一个门都是由上一时刻 h t − 1 h_{t−1} ht−1和当前时刻 x t x_t xt进行融合后,在经过 σ \sigma σ产生一个0-1的控制量。
1.4.2 LSTM:Input gate and Cell state
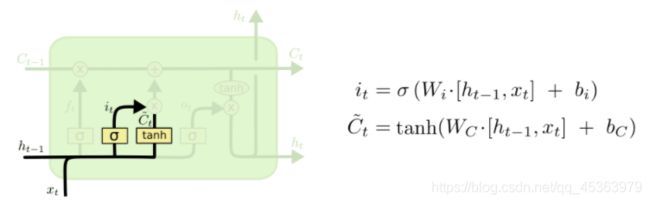
下一步我们将决定有哪些新的信息将要被存储到cell state,这里有两个部分。首先,输入门是由sigmoid层决定有哪些信息需要更新,tanh层创建新的后选向量 C t ~ \tilde{C_t} Ct~,他将被添加到状态中,在下一步,就是将 i t i_t it和 C t ~ \tilde{C_t} Ct~进行结合以更新cell state
在我们的语言模型示例中,我们希望将新主语的性别添加到cell state中,以替换我们忘记的旧的性别。
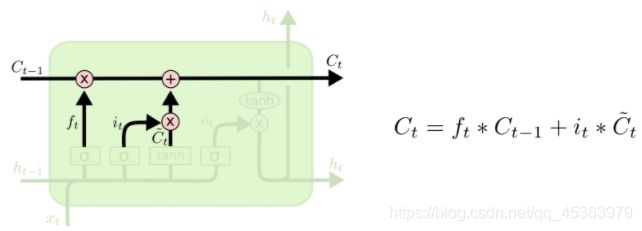
输入门施加在新的信息上,忘记门施加在了过去的信息上。现在我们的到了过滤后的历史信息,和过滤后的新的信息然后进行相加融合
h t − 1 h_{t−1} ht−1和 x t x_t xt x ^ \hat x x^
1.4.3 LSTM:Output gate

值得注意的是,这里的 h t h_t ht不要像之前RNN中的那样理解为memory,在LSTM中将其理解为输出。而 C t C_t Ct则是memory。
最后,我们要决定输出是什么,这个输出是基于cell state的状态。首先将cell state的通过tanh压缩到-1~1之间,再将其乘以sigmoid输出门的输出( O t O_t Ot决定cell state那部分应该输出)进行相乘,这样我们就能决定哪些部分被输出。
1.5 LSTM如何解决梯度消失
首先我们回顾RNN产生梯度消失的原因。

当 W R W_R WR大于1出现梯度爆炸,小于1出现梯度消亡。
而LSTM的是如何解决的呢?

现在如果我们想往回传播k时间步长,我们简单地把这些项乘以k次,因此有累加的情况就会大大降低出现趋近于0或者∞的情况。请注意这个递归梯度和普通RNNs的梯度之间的巨大区别,因为RNN是K次幂。
2. LSTM Layer使用
2.1 nn.LSTM
__init__
input_size – word embedding的维度,100维的向量表示一个单词,inputsize=100
hidden_size – 用来表示memory
num_layers – 默认为1
out,(ht,ct) = forward(x, [ht_0, ct_0]) 其中ht_0, ct_0为最开始ht和ct的状态
X=[seq_len, batch, feature_len]
h/c=[number_layers, batch, hidden_len]
out=[seq_len, batch, hidden_len]
code:
lstm = nn.LSTM(input_size=100, hidden_size=20, num_layers=4)
x = torch.randn(10, 3, 100)
out, (h, c) = lstm(x) # 当h0和c0默认为0可以省略掉
print('out shape', out.shape)
print('ht shape', h.shape)
print('ct shape', c.shape)
运行结果:
out shape torch.Size([10, 3, 20])
ht shape torch.Size([4, 3, 20])
ct shape torch.Size([4, 3, 20])
2.1 nn.LSTMCell
__init__
input_size – word embedding的维度,100维的向量表示一个单词,inputsize=100
hidden_size – 用来表示memory
num_layers – 默认为1
ht,ct = forward(xt, [ht_0, ct_0])
Xt = [batch, feature_len] 送seq_len次
ht/ct = [batch, hidden_len]
One layer lstm code:
# One layer lstm
cell = nn.LSTMCell(input_size=100, hidden_size=20)
x = torch.randn(10, 3, 100)
h = torch.zeros(3, 20)
c = torch.zeros(3, 20)
for xt in x:
h, c = cell(xt, [h, c])
print('ht shape', h.shape)
print('ct shape', c.shape)
运行结果:
ht shape torch.Size([3, 20])
ct shape torch.Size([3, 20])
Two layer lstm code
# Two layer lstm
cell1 = nn.LSTMCell(input_size=100, hidden_size=30)
cell2 = nn.LSTMCell(input_size=30, hidden_size=20)
x = torch.randn(10, 3, 100)
h1 = torch.zeros(3, 30)
c1 = torch.zeros(3, 30)
h2 = torch.zeros(3, 20)
c2 = torch.zeros(3, 20)
for xt in x:
h1, c1 = cell1(xt, [h1, c1])
h2, c2 = cell2(h1, [h2, c2])
print('h1 shape', h1.shape)
print('c1 shape', c1.shape)
print('h2 shape', h2.shape)
print('c2 shape', c2.shape)
运行结果:
h1 shape torch.Size([3, 30])
c1 shape torch.Size([3, 30])
h2 shape torch.Size([3, 20])
c2 shape torch.Size([3, 20])
3. 感情分类实战
# -*- coding: utf-8 -*-
"""lstm
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1GX0Rqur8T45MSYhLU9MYWAbycfLH4-Fu
"""
# !pip install torch
# !pip install torchtext
# !python -m spacy download en
# K80 gpu for 12 hours
import torch
from torch import nn, optim
from torchtext import data, datasets
print('GPU:', torch.cuda.is_available())
torch.manual_seed(123)
TEXT = data.Field(tokenize='spacy')
LABEL = data.LabelField(dtype=torch.float)
train_data, test_data = datasets.IMDB.splits(TEXT, LABEL)
print('len of train data:', len(train_data))
print('len of test data:', len(test_data))
print(train_data.examples[15].text)
print(train_data.examples[15].label)
# word2vec, glove
TEXT.build_vocab(train_data, max_size=10000, vectors='glove.6B.100d')
LABEL.build_vocab(train_data)
batchsz = 30
device = torch.device('cuda')
train_iterator, test_iterator = data.BucketIterator.splits(
(train_data, test_data),
batch_size = batchsz,
device=device
)
class RNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim):
"""
"""
super(RNN, self).__init__()
# [0-10001] => [100]
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# [100] => [256]
self.rnn = nn.LSTM(embedding_dim, hidden_dim, num_layers=2,
bidirectional=True, dropout=0.5)
# [256*2] => [1]
self.fc = nn.Linear(hidden_dim*2, 1)
self.dropout = nn.Dropout(0.5)
def forward(self, x):
"""
x: [seq_len, b] vs [b, 3, 28, 28]
"""
# [seq, b, 1] => [seq, b, 100]
embedding = self.dropout(self.embedding(x))
# output: [seq, b, hid_dim*2]
# hidden/h: [num_layers*2, b, hid_dim]
# cell/c: [num_layers*2, b, hid_di]
output, (hidden, cell) = self.rnn(embedding)
# [num_layers*2, b, hid_dim] => 2 of [b, hid_dim] => [b, hid_dim*2]
hidden = torch.cat([hidden[-2], hidden[-1]], dim=1)
# [b, hid_dim*2] => [b, 1]
hidden = self.dropout(hidden)
out = self.fc(hidden)
return out
rnn = RNN(len(TEXT.vocab), 100, 256)
pretrained_embedding = TEXT.vocab.vectors
print('pretrained_embedding:', pretrained_embedding.shape)
rnn.embedding.weight.data.copy_(pretrained_embedding)
print('embedding layer inited.')
optimizer = optim.Adam(rnn.parameters(), lr=1e-3)
criteon = nn.BCEWithLogitsLoss().to(device)
rnn.to(device)
import numpy as np
def binary_acc(preds, y):
"""
get accuracy
"""
preds = torch.round(torch.sigmoid(preds))
correct = torch.eq(preds, y).float()
acc = correct.sum() / len(correct)
return acc
def train(rnn, iterator, optimizer, criteon):
avg_acc = []
rnn.train()
for i, batch in enumerate(iterator):
# [seq, b] => [b, 1] => [b]
pred = rnn(batch.text).squeeze(1)
#
loss = criteon(pred, batch.label)
acc = binary_acc(pred, batch.label).item()
avg_acc.append(acc)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i%10 == 0:
print(i, acc)
avg_acc = np.array(avg_acc).mean()
print('avg acc:', avg_acc)
def eval(rnn, iterator, criteon):
avg_acc = []
rnn.eval()
with torch.no_grad():
for batch in iterator:
# [b, 1] => [b]
pred = rnn(batch.text).squeeze(1)
#
loss = criteon(pred, batch.label)
acc = binary_acc(pred, batch.label).item()
avg_acc.append(acc)
avg_acc = np.array(avg_acc).mean()
print('>>test:', avg_acc)
for epoch in range(10):
eval(rnn, test_iterator, criteon)
train(rnn, train_iterator, optimizer, criteon)
4. Reference
1.Understanding LSTM Networks
2.Why LSTMs Stop Your Gradients From Vanishing: A View from the Backwards Pass
3.Lecture 15: Exploding and Vanishing Gradients